多元函數最值問題求解策略續

☉湖北省武漢市第二中學 朱九如

多元函數最值問題求解策略續

☉湖北省武漢市第二中學 朱九如

文1中提出了求解多元函數最值問題的10種方法，舉例給出了其中的7種方法，讀后深受啟發，本文舉例給出另外的幾種求解方法.

一、減元法

根據轉化與化歸思想的理論，嘗試將多元函數問題轉化為我們熟悉的一元函數來處理，可通過換元、不等式放縮技巧、題中條件等式等途徑實現.

1.通過換元減元

例1 設x，y∈R+，x+y=c，c為常數且c∈（0，2］，求u=）的最小值.

解析：

例2 設a，b∈R，a2+2b2=6，則a+b的最小值是________.

解析：因為a，b∈R，a2+2b2=6，所以令則，所以a+b的最小值是-3.

評注：換元法是指通過引入一個或幾個新的變量，來替換原來的某些變量（或代數式），使問題得以解決的一種數學方法.在解題中，常常使用的換元法有兩類，即代數換元和三角換元，我們可以根據具體問題及題目形式靈活選擇換元的方法，以便將復雜的函數最值問題轉化為簡單的函數最值問題.在使用換元法時，要特別注意換元后新元的取值范圍.

2.通過放縮減元

解析：于是當且僅當時，等號成立.

評注：本題利用三角函數中正、余弦值的有界性，選取適當的不等式進行放縮使得問題得以解決.

3.利用條件減元

例4設x，y為實數，已知5x2+4y2=10x，則4（x2+y2）的最大值為_________.

解析：已知5x2+4y2=10x，可得4y2=10x-5x2≥0，所以0≤x≤2.

所以4（x2+y2）=10x-x2=25-（5-x）2≤25-32=16?x2+y2≤4.

評注：本題根據題中的關系式將二元函數轉化為我們熟悉的一元函數，利用配方法將問題解決.本題中消去變量y比較方便，不過要注意變量x的取值范圍.

二、判別式法

如果通過代換及題中關系等式可得到一個關于某個變量的一元二次方程，則利用二次方程有解判別式非負可以將問題解決.

例5已知a，b，c滿足a+b+c=0，a2+b2+c2=1，則a的最大值是________.

解析：將c=-（a+b）代入a2+b2+c2=1，得2b2+2ab+2a2-1=0.此關于b的方程有實數解，則Δ=（2a）2-8（2a2-1）≥0，整理得即，所以a的最大值是

評注：將兩個已知條件中的a消去，整理成關于b的一元二次方程，由于方程有實數解，判別式恒大于或等于0，得到關于a的不等式，求解后即得a的最大值.

三、分類討論法

例6 若實數x，y滿足x2+y2≤1，則|2x+y-2|+|6-x-3y|的最小值是_______.

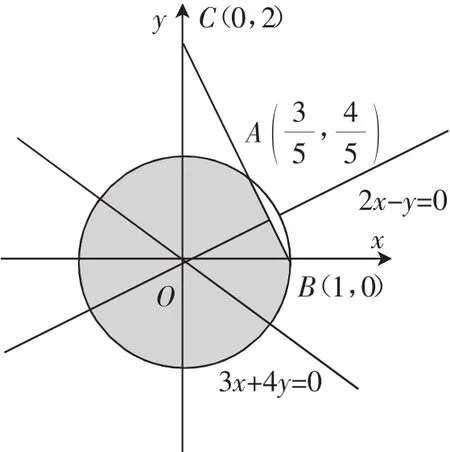
圖1

解析：x2+y2≤1表示圓x2+y2=1及其內部，易得直線6-x-3y與圓相離，故|6-x-3y|=6-x-3y，當2x+y-2≥0時，|2x+y-2|+|6-x-3y|=x-2y+4，如圖1所示，可行域為小的弓形內部，目標函數z=x-2y+4，可知，當時，zmin=3. 當2x+y-2＜0時，|2x+y-2|+|6-x-3y|=8-3x-4y，可行域為大的弓形內部，目標函數z=8-3x-4y，同理可知，當時，z=3.綜上所述，|2x+y-2|+|6-x-3y|的最min小值是3.

評注：本題根據可行域是圓及其內部的特點，結合直線與圓的位置關系的判定，首先可以將目標函數中的兩個絕對值號去掉一個，再利用分類討論的數學思想去掉一個絕對值號，利用線性規劃知識求解.

例7（2005年全國高中數學聯賽福建賽區預賽）設a、b、c是正整數，關于x的一元二次方程ax2+bx+c=0的兩個實根的絕對值均小于，求a+b+c的最小值.

解析：設方程的兩個實根為x1、x2，由韋達定理知x1＜0，x2＜0.

（1）當b=7時，由4a≤4ac≤b2及a≥11，知a=11或12，c=1.

由于方程11x2+7x+1=0有根不合題意；方程12x2+7x+1=0的兩根為，也不合題意.

（2）當b=8時，由4ac≤b2=64及a≥11，知a=11，12，13，14，15，16，c=1.

而f（15）=0，因此，a只能為16. 此時，a+b+c=25，而16x2+8x+1=0的兩根為滿足題意.

若a+b+c＜25，則只能是a=14，b=9，c=1.此時，方程14x2+9x+1=0的兩根為，不合題意.故a+b+c≥25.

綜上，a+b+c的最小值為25.

評注：對于離散型條件最值，求解時常常對離散變量進行分類討論，采用窮舉的方法確定最值.

1.范東暉.分類例談多元函數最值問題求解策略［J］.中學數學（上），2017（10）.