復合函數求導方法的探究與應用

☉湖北省宜昌市第一中學 鄭璇玥

復合函數求導方法的探究與應用

☉湖北省宜昌市第一中學 鄭璇玥

復合函數求導在導數的運算中扮演者重要的角色，在平常的學習中，求導并不意味著對初等函數的求導.但是能否對初等函數進行精確求解，決定著是否能對復合函數進行正確的求解.因為不論是在高等數學還是目前的高中數學中的復合函數求導，不僅有基本初等函數的四則運算，還包括基本初等函數的復合.所以復合函數的分解與求解步驟是學習的重點.

一、復合函數的認識

一般地，對于兩個函數y=f（u）和u=g（x），如果通過變量u，y可以表示成x的函數，那么稱這個函數為函數y=f（u）和u=g（x）的復合函數，記為y=f［g（x）］.其中x成為自變量，u為中間變量，y為因變量.不是任何函數都能復合成一個復合函數，只有當u=g（x）的值域含于y=f（u）的定義域時，二者才能合成一個復合函數.［1］

由此我們可以知道，復合函數運算的對象雖然是變量y關于變量x的函數關系，但是其實早已不是僅對x進行簡單的運算，而是需要關系到含有x的中間變量的運算上.所以對復合函數中含有x的式子的理解顯得尤為重要.

二、復合函數的求解

1.圖式表示法

為了方便理解復合函數的求導方法，需要明確函數結構內部變量間的關系，在此可以先利用畫圖來幫助理解.“樹形圖”如圖1所示.［2］

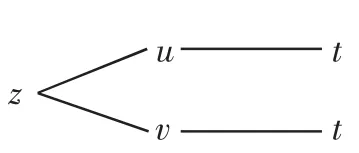
圖1

從圖中可以清晰的看到，自變量、因變量、中間變量的分工情況及函數的從屬關系.出現在“樹形圖”中樹枝末端的變量為自變量.如圖1所示，樹枝末端變量只有一個，那就是t，則t是自變量，z是t的一元函數.

2.復合函數的求導法則

相比高中課本中的求導法則，引入偏導數與微分的概念更加便于理解復合函數求導的步驟與方法.

如果函數u=φ（t），v=Φ（t）都在點t處可導，函數z=（fu，v）在對應點（u，v）具有連續的一階偏導數，則復合函數z=［fφ（t），φ（t）］在點t可導，且

其中z=［fφ（t），Φ（t）］僅是t的一元函數，則這里的稱為全導數.［3］

結合圖1，可以看到z經過t的線路有兩個，即路徑”z—u—t”和路徑”z—v—t”與等式①對應，即

三、復合函數求導中易出現的問題

由于對初等函數求導的基礎知識掌握不牢固，經常會出現各種問題，在此對幾種典型的錯誤進行歸納.

例1設求y′x.［4］

錯解：

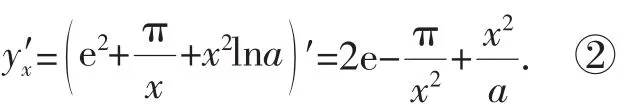
錯解分析：本題的錯誤原因是基本初等函數掌握并不牢固，致使常數求導（d2）′=0，（lna）′=0錯誤的使用了指數、對數函數的求導公式.

正解：③

例2設，求y′x.［5］

錯 解 ：

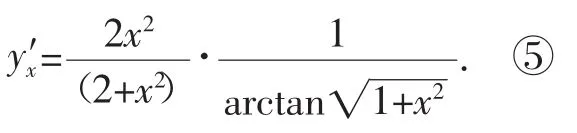
錯題分析：復合函數的復合過程應為y=lgu，u=

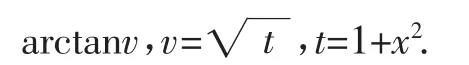
正解

明顯在錯解中忽略了其中一步，致使求導出錯.求解復合函數的導數，關鍵要弄清復合函數是由哪些基本初等函數或者簡單函數復合而成，按照復合次序從外向內進行求導.所以注意復合函數的分層并且牢記“公式是基礎，分層是關鍵”才是解題的關鍵.

四、復合函數的常用解題技巧

根據等式①，首先要清楚地分析復合函數的關系，找出要求導的復合函數是由哪幾個初等函數組成的，然后再設置恰當的中間變量，把它分解成一些基本的初等函數的復合，最后由最外層開始，先使用法則，后使用導數的基本公式，由表及里一層一層求導，切記千萬不可忘記里層的求導.根據以上的解題步驟，下面介紹一些求導的常用技巧.

1.冪指函數求解方法

例3求復合函數的導函數.［6］

解析：第一步，先對函數兩邊取對數，從而得到lny=

對數求導法則對一些冪函數，特別是乘積形式函數這類復雜的復合函數的求導顯得十分便捷.在求解時對函數式兩邊取對數，然后對此對數式兩邊同時對x求導，但要注意在解題時，（fx）≠0時，而不是因為這一類復合函數求解十分煩瑣，所以對這些式子需要進行化簡、移項，確保得到最簡潔、最精確的答案.

2.反序求導法復合函數的導數

反序求導法，其實是一種對復合函數從里到外一次求導的方法，它和上述的求導方法有相似性，但是其實質卻有不同.反序求導法具有以下三個要點：第一，求導次序和求復合函數值的次序一致，方便上手，有助于對此方法的掌握和運用；第二，從里到外求導，避免了求導不徹底的問題；第三，形式上便于書寫.

求導形式：通常由函數y=（fu），u=φ（x）構成的復合函數y=［fφ（x）］的導數時，是應用復合函數求導法則y′x=f′（uu）·φ（′x），從外到內求導；而反序求導則是y′x=φ（′x）·f′（uu），從里到外進行求導.下面進行舉例說明：

例4求復合函數y=e-2x的導數.

解析：設y=eu，u=-2x，與反序求導法則相對應：y′x=φ（′x）·f′（uu），由內向外進行求導.u′=-2，y′=eu.

分析求導后進行數據整理后得到結果為y′=u′·（eu）′=-2e-2x.

五、總結

復合函數存在不同的種類，只有準確地把握函數內部結構的關系，才能有效地解決復合函數的求導問題.本文通過對復合函數的錯題分析，同時也介紹相關的求解技巧.然而，復合函數的求解技巧遠不止本文所列舉的這些，由于篇幅有限，本文不再贅述.總之，熟練地掌握初等函數的求導法則，為求解復合函數打下牢固的基礎，勤加練習才能減少出錯的概率.

1.高一數學必修1［M］.北京：人民教育出版社，2015.

2.張曉妮.多元復合函數的求導方法研究［J］.科技教育，2016.

3.同濟大學數學系編.高等數學下冊［M］.北京：高等教育出版社，2013（4）.

4.張樹林.一元復合函數求導法則及常見錯誤剖析［J］.科技視界，2015.

5.張月華.復合函數求導探析［J］.漯河職業技術學院學報，2011（2）.

6.毛濤.復合函數求導方法和技巧［D］.陜西理工學院，2015.