例談高中解題的幾種策略

☉江蘇省沭陽高級中學 錢文奇

例談高中解題的幾種策略

☉江蘇省沭陽高級中學 錢文奇

數學解題的教與學是數學教學的主要內容，數學解題能力是學生數學的核心能力，也是數學教學的著重點.在高中數學學習中，解題是高中數學學習的一個重要部分，也是很多學生困惑的地方.因為學生總感覺聽懂了，題卻解不出來.下面筆者結合多年的教學經歷，談談高中解題的幾種策略，以期拋磚引玉.

策略一、挖掘題目隱含條件

在求解數學問題的過程中，有些題目條件設置得很隱蔽，若不能很好挖掘使用，就很難正確解出結果.這就要求我們在解題中有意識地注意挖掘隱含條件，充分利用好所給的條件解題.

1.挖掘概念中的隱含條件

不少數學問題往往會在數學概念上設置障礙，若學生對概念理解不深刻，就很難觀察到其中隱含的障礙.因此要解決好這類問題，必須對概念深入理解.

例1 已知l1：2x+my-2=0，l2：mx+2y-1=0，并且l1⊥l2，則m=______.

錯解：有些同學認為l1⊥l2，則有k1·k2=-1，而由無解.

上述學生解錯的原因就在于對線線垂直概念的不理解.結論“l1⊥l2，則k1·k2=-1”的前提的兩條直線的斜率都存在.因此需要對斜率不存在的情況進行討論.

正解：若m=0，顯然l1⊥l2；若m≠0，則由l1⊥l2，得k1·k2=-1，而由矛盾，m不存在.于是m=0.

2.挖掘解題思維中的隱含條件

有的問題若按照常規思路來解決，則往往過程繁雜，無法解出.這時就需要轉換思維，充分利用條件，有效解決問題.

例2設集合A=｛（x，y）|x=n，y=an+b，n∈Z｝，B=｛（x，y）|x=m，y=3m2+15，m∈Z｝，C=｛（x，y）|x2+y2≤144｝，問是否存在實數a，b，使下列條件同時成立？（1）A∩B≠?；（2）（a，b）∈C.

錯解：由條件（1）

在x∈Z時有解，消去y，得

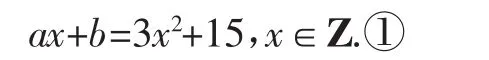
由條件（2）（a，b）∈C，得

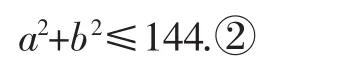
此題中常規思路就是將x視為變量，（a，b）視為常量，于是把①式視為關于x的一元二次方程，轉化為關于x有整數解的問題，按照此思路，大多數同學束手無策，望而卻步，無法正確解出結果.不妨轉換思維角度，將（a，b）視為變量，把x視為常量，則可以將原問題轉化為直線與圓面在整數范圍內是否有公共點的問題.于是由d=得（x2-3）2≤0，從而只有顯然與x∈Z矛盾，故滿足條件的a，b不存在.

正解：由于（1）A∩B≠?；（2）（a，b）∈C同時成立，有解且a2+b2≤144，

即3x2-ax+15-b=0有解且a2+b2≤144，

則Δ=a2-12（15-b）=a2+12b-180≥0，且a2+b2≤144，

即180-12b≤a2≤144-b2，

故180-12b≤144-b2?b2-12b+36≤0，即（b-6）2≤0，

因此存在a，b滿足條件.

策略二、跨越思維斷層處障礙

在高中數學解題中，常常會有以下情景：遵循課本上所教講的概念、公式、方法等，但是用著用著就會突然出現頭腦里一片空白的情況.再去翻閱資料，會有一些提示，按照提示，問題就很容易解決，但是我們當時就是無法想出這個提示，即無法跨越這個思維的高度，也就是思維在這個點出現了斷層.下面通過一道題談談如何跨越這種思維斷層處的障礙.

例3設函數曲線y=（fx）在點（1，（f1））處的切線方程為y=e（x-1）+2.

（1）求a，b；

（2）證明：（fx）＞1.

解：（1）函數（fx）的定義域為（

由題意得（f1）=2，f（′1）=e，故a=1，b=2.

設函數g（x）=xlnx，則g（′x）=1+lnx，所以當）時，g（′x）＜0，

故h（x）在（0，1）上單調遞增，在［1，+∞）上單調遞減，從而h（x）在（0，+∞）上的最大值為

綜上所述，當x＞0時，g（x）＞h（x），即（fx）＞1.

學生拿到此題，都能想到用求導解決，但是很多學生在把（fx）＞1轉化為再變形成，再構造函數，求導數得令g（′x）=0，到這步后大多數學生無法解出，就是想不到將lnx與ex分離，即所謂出現了思維斷層.在平時的教學中，應該要時刻警惕概念教學中的“滑過現象”，在解題中不斷積累獲取信息的能力，重視解題過程的教學，引導學生不斷積累解題經驗，加強教學反思，提高學生的解題能力.

策略三、注重解題后的反思與優化

解題過程中，學生較大限度地發揮了自身的數學水平，解題后老師及時了解學生的主要解題思路和解題阻滯點，在解法基礎上設計好優化方案，挖掘出試題的本質特征，優化學生的解題方法，從而提升學生數學解題能力.

例4設函數（fx）=x|x-a|+b，a，b∈R.

（1）當a=2時，求函數（fx），x∈［1，2］的值域；

（2）對于給定的實數a（a≥2），存在實數b，對于任意實數x∈［1，2］，都有不等式|（fx）|≤1恒成立，求實數a

2的取值范圍.

針對第（2）問，學生作業中的解法如下：

解法1：由于，故由閉區間上二次函數的性質

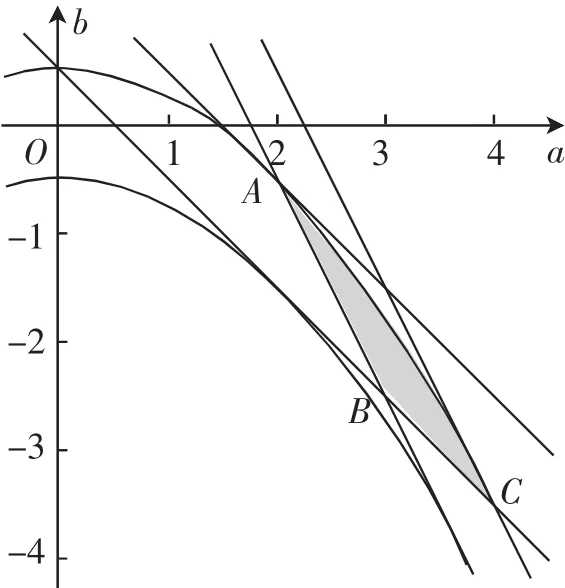
圖1

解法2：由于，故命題“存在實數b對于任意實數x∈［1，2］，都有不等式|（fx）恒成立”等價于“當

由于二次函數最值必在x=1，2，a處取到，據此展開2討論

故a的取值范圍為2≤a≤3或3＜a≤4，即2≤a≤4.

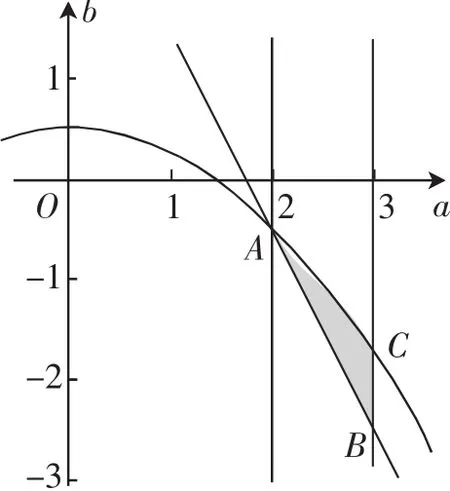
圖2

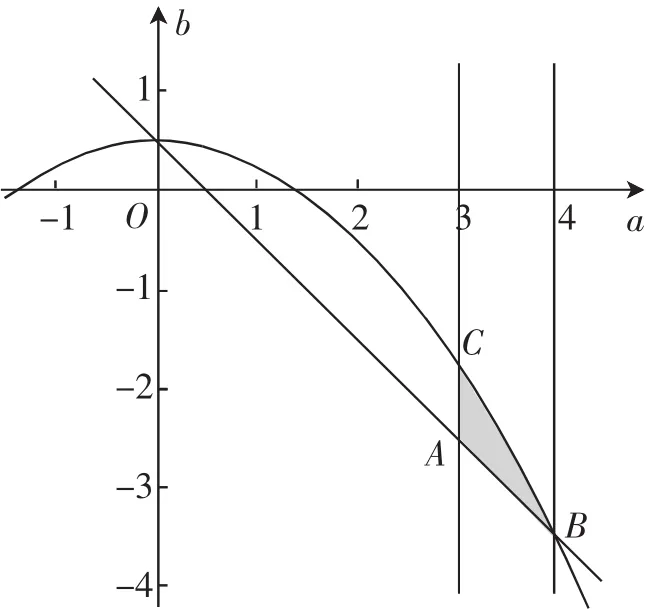
圖3

這兩種解法，可操作性強，但是運算量大，解題過程復雜，學生真正解出的很少.因此解題后可以引導學生對這兩種解法進行優化.

解法1的優化：

同理利用不等式運算性質消去b，由④⑥可得2≤a≤6；由⑤⑥可得2≤a≤4，取三者交集得2≤a≤4.

故a的取值范圍為2≤a≤4.

運用必要條件先縮小參數范圍，減少了分類討論的情況，大大簡化了原解法.

由此可見，題后反思是學生所思和所想的自然延伸，跟隨思維的發展進程，師生不斷進行提煉和優化，這種由表及里、由粗到細，伸展不同方向的觸角的解題分析方法，對提升學生的數學解題能力是大有裨益的.