奇、偶項為不同數列型問題的探究

☉江蘇省徐州市第三中學 趙 勇

奇、偶項為不同數列型問題的探究

☉江蘇省徐州市第三中學 趙 勇

在處理奇數項與偶數項為不同類型的數列求通項公式或前n項和中，由于學生在進行奇、偶討論時經常會錯把n當成了奇數項數列、偶數項數列的項數，從而產生錯解.下面通過舉例，對此類問題進行詳細探究，以期對學生解答此類問題有所有助，從而有效避錯.

題目已知由整數組成的數列｛an｝各項均不為0，其前n項和為Sn，且a1=a，2Sn=anan+1.

（1）求a2的值；

（2）求｛an｝的通項公式；

（3）若n=15時，Sn取得最小值，求a的值.

一、通項問題

第（1）問，較為簡潔，直接利用賦值法即可求解.

因為2Sn=anan+1，所以2S1=a1a2，即2a1=a1a2，因為a1=a≠0，所以a2=2.

第（2）問，給出與前n項和Sn有關的關系式，通常利用公式求解.本題也不例外.

因為2Sn=anan+1，所以2Sn-1=an-1a（nn≥2），兩式相減，得到2an=a（nan+1-an-1）.因為an≠0，所以an+1-an-1=2.所以｛a2k-1｝，｛a2k｝都是公差為2的等差數列.

此時學生易給出錯誤答案：

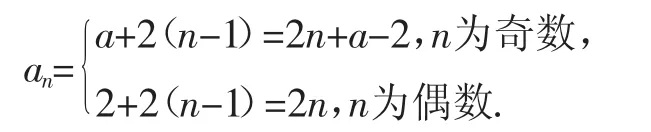
原因是機械地套用了等差數列通項公式，錯誤地認為奇數項與偶數項的項數均為n.

為了充分認識錯誤的原因，我們可列舉數列的有限項，當n為奇數時，如取n=11，得a，2，a+2，4，a+4，6，a+6，8，a+8，10，a+10，則奇數項為a，a+2，a+4，a+6，a+8，a+10，共6項，并不是10，項數所以當n為奇數時，

同理，當n為偶數時，如取n=10，得a，2，a+2，4，a+4，6，a+6，8，a+8，10，則偶數項為2，4，6，8，10，共5項，項數為所以當n為偶數時

二、求和問題

奇數項與偶數項為不同類型的數列求和問題，應對奇數項與偶數項分別求和，再相加.求解中注意對奇數項數列與偶數項數列項數的準確把握.

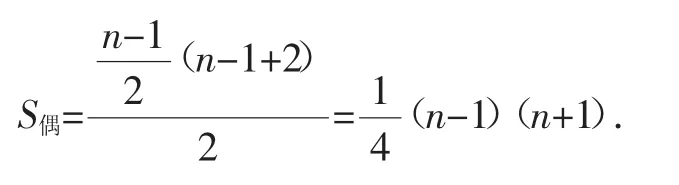
三、求最值

數列的最值問題，以等差數列為例，若首項為正，且公差小于0，則前n項和有最大值，此時n的值可由an≥0求解.同理，若首項為負，且公差大于0，則前n項和有小值，此時n的值可由an＜0求解.當然也可以利用前n項和的二次函數性質來求解.

第（3）問，方法1：因為2Sn=anan+1，由（2）知，an=

注意到所有奇數項構成的數列是一個單調遞增的，所有偶數項構成的數列是一個單調遞增的.

當n為偶數時，an＞0，所以此時Sn＞Sn-1，所以S15為最小值等價于S13≥S15，S15≤S17，所以a14+a15≤0，a16+a17≥0，所以14+15+a-1≤0，16+17+a-1≥0，解得-32≤a≤-28.

因為數列｛an｝是由整數組成的，所以a∈｛-32，-31，-30，-29，-28｝.

又因為an≠0，所以對所有的奇數n，an=n+a-1≠0，所以a不能取偶數，所以a=-31，或a=-29.

方法2：因為S15為最小值，此時n為奇數，當n為奇數時，根據二次函數的性質知道，有，解得-32≤a≤-28.

因為數列｛an｝是由整數組成的，所以a∈｛-32，-31，-30，-29，-28｝.

又因為an≠0，所以對所有的奇數n，an=n+a-1≠0，所以a不能取偶數，所以a=-31，或a=-29.

經檢驗，此時Sn為最小值，所以a=-31，或a=-29.

變式探究：若數列｛an｝滿足an+1+（-1）nan=2n-1，則數列｛an｝的前60項和為__________.

解析：本題是填空題，故可以采用歸納的方法來尋找解題規律，當然它也可以用迭代法來求解.

由題意可知，a2-a1=1，a3+a2=3，a4-a3=5，a5+a4=7，…，所以a3+a1=2，a4+a2=8，a7+a5=2，a8+a6=24，…，從第一項開始，依次取2個相鄰奇數項的和等于2，從第二項開始，依次取2個相鄰偶數項的和構成以8為首項，以16為公差的等差數列，所以

綜上，解決奇數項與偶數項為不同數列問題的思想方法主要有分類討論思想、整體思想和等價轉化思想，具體求解中，通常需要利用列舉、合情推理或迭代的方法來尋找相鄰幾項的規律，進而明確數列問題的本質.