例談高考中的含參問題

☉寧夏銀川二中 馬麗欣

例談高考中的含參問題

☉寧夏銀川二中 馬麗欣

含參問題是近幾年高考中的熱點，也是重點.此類試題考查的知識點綜合度比較高，難度比較大.下面筆者通過自己的教學實踐，談談高考對含參問題的考查，以拋磚引玉.

一、運用單調性解決含參問題

有的題目利用洛必達法則解決比較簡便，我們先介紹一下洛必達法則：

對-∞＜a＜b＜+∞，設（fx）和g（x）是兩個實數值函數，并都在［a，b］上連續，在（a，b）上可微且在（a，b）上g′（x）≠0，如果在（a，b）上遞增（遞減），那么函數F（x）=和也在（a，b）上遞增（遞減）.而且，如果的單調性是嚴格的，那么F（x）和G（x）的單調性也是嚴格的.

證明：只需證明F（x）的情形，G（x）同理可得.不妨設在（a，b）上遞增，g（′x）在（a，b）恒小于零.

由柯西中值定理可知，對于任意的x∈（a，b），總存在y∈（a，x），使得：

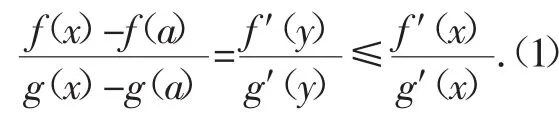
由于g′（x）＜0，x∈（a，b），故有g（x）-g（a）＜0，且［g（x）-g（a）］g（′x）＞0（.2）

在（1）式兩端同時乘以（2）式，有：

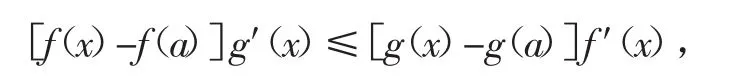
例1設函數（fx）=ln（x+1）+a（x2-x），其中a∈R.

（1）略；

（2）若?x＞0，（fx）≥0成立，求a的取值范圍.

解：對成立，等價于

從而F（x）也在（1，+∞）上單調遞增，

所以有a≥0.

二、通過分類討論確定參數的取值范圍

例2設函數（fx）=ln（x+1）+a（x2-x），其中a∈R.

（1）討論函數（fx）極值點的個數，并說明理由；

（2）若?x＞0，（fx）≥0成立，求a的取值范圍.

分析：本題是一道函數與導數的綜合問題，有一定的難度和較好的區分度.第（1）問屬于求函數極值問題，通過導數研究函數單調性，很好地考查了考生分類討論思想在解題中的應用，雖然求解比較煩瑣，但大多數考生都能接受，屬于常規題.具體解法略.當時，（fx）的無極值點；當a＜0時，（fx）有一個極值點；當時，（fx）的有兩個極值點.

此問實際上是恒成立中的參數取值問題，為了幫助同學們解決此類問題，下面將從不同視角進行求解.

解法1：由（1）可知，①當時，（fx）在（0，+∞）單調遞增，而（f0）=0，則當x∈（0，+∞）時，（fx）＞0，符合題意；

③當a＞1時，g（0）＜0，x2＞0，所以函數（fx）在（0，x2）單調遞減，而（f0）=0，則當x∈（0，x2）時，（fx）＜0，不符合題意；

④當a＜0時，設h（x）=x-ln（x+1），當x∈（0，+∞）時，在（0，+∞）單調遞增，因此，當x∈（0，+∞）時，h（x）＞h（0）=0，ln（x+1）＜0，于是，（fx）＜x+a（x2-x）=ax2+（1-a）x，當時，ax2+（1-a）x＜0，此時f（x）＜0，不符合題意.

綜上所述，a的取值范圍是0≤a≤1.

本解法主要從研究函數的單調性入手，考生通常出錯在分類討論的情況較為復雜時，思路上不夠十分清晰、條理，造成思維混亂，難以抽身.

三、通過分離參數確定參數取值范圍

分離參數法是求解參數取值的比較常見的方法之一，對于例2的求解當然也可以利用此法，但本題的在于巧妙用上教材中習題的一個結論（?x＞0，均有ln（x+1）＜x成立）方可使得問題得以順利求解.

解法2：設函數（fx）=ln（x+1）+a（x2-x），?x＞0，都有（fx）≥0成立，即ln（x+1）+a（x2-x）≥0.

由于?x＞0均有ln（x+1）＜x成立，其證明如下：

當x＞0時，h（′x）＜0，h（x）單調遞減，h（x）＜0，ln（x+1）-x＜0，即ln（x+1）＜x.

①當x=1時，ln2≥0恒成立；

綜上可知，對于?x＞0，都有（fx）≥0成立，只需0≤a≤1即可，故所求a的取值范圍是0≤a≤1.

本解法主要借助分離參數法進行求解，眾多考生都能想到這一求解辦法，但都是因為分離參數后所得到的函數較為復雜，直接利用函數導數求解甚是復雜，于是無從研究其單調性和確定所求參數取值范圍，進而望而生嘆.又如下面的試題：

例3 設函數f（x）=ax-2x+2對于滿足1＜x＜4的一切x都有（fx）＞0，求實數a的取值范圍.

分析：此題中只含有一個參數a，屬于恒成立問題.如果從二次函數的角度考慮，需要對參數a進行分情況討論，結果就很麻煩.如果將參數a進行分離，則變為求已知函數的最值問題，就比較好辦.

解：由ax-2x+2＞0，得則

當x∈（1，2）時，g′（x）＞0，g（x）是單調遞增的；

當x∈（2，4）時，g′（x）＜0，g（x）是單調遞減的.所以，當x=2時，g（x）有極大值

四、利用線性規劃解決參數取值范圍問題

例4 在平面直角坐標系xOy中，設A，B，C是圓x2+y2=1上的相異三點，若存在正實數λ，μ使得向量則λ2+（μ-3）2的取值范圍是_______.

分析：此題中A，B，C是三個動點，結果含有兩個參數正實數λ，μ，若以λ為橫坐標，μ為縱坐標，則所求結果為點（λ，μ）到點（0，3）的距離的平方可能取到的范圍.

解：平方后可得到—

即1=λ2+μ2+2λμcosθ.設θ是向量OA與OB的夾角，則θ∈（0，π）.

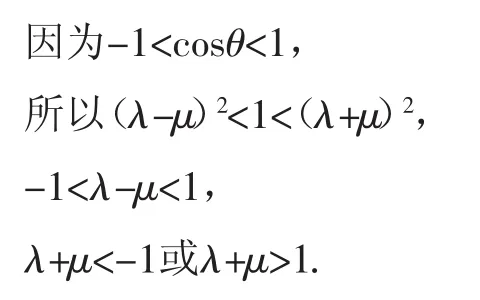
以λ為橫坐標，μ為縱坐標，可以表示出滿足上述條件的平面區域，即可行域.

確定區域內的點到（0，3）的距離的平方可能取到的范圍：點（0，3）到直線λ-μ+1=0的距離為最小值，

所以，λ2+（μ-3）2的取值范圍是（2，+∞）.

五、利用求導法解一類求參數取值范圍

有些求參數的取值范圍的問題是比較復雜的，涉及分類談論思想，往往利用求導解決相對比較簡便，進而得到參數的取值范圍.

例5設函數，若對所有的x≥0，都有（fx）≤ax，求實數a的取值范圍.

解 ：設，所以

例6設函數（fx）=ex+sinx-1-2x-ax2，若當x≥0時，（fx）≥0恒成立，求a的取值范圍.

解：可得f（′x）=ex+cosx-2-2ax，f（″x）=ex-sinx-2a，

用兩次求導及不等式x＞sinx，ex≥x+1（x≥0）可證所以當時，（fx）≥0（x≥0）成立.

通過以上幾個例題可以看出，在解決含有參數的問題時，可以根據題目中所含參數的個數來選擇解題方法，有時能夠達到事半功倍的效果.當然，什么問題都不是絕對的，這就要求我們遇到數學問題時，要具體問題具體分析，要注意挖掘數學知識間的內在聯系，同時，要善于總結、歸納，注重提煉方法.只有這樣我們才能更好地學好數學.