利用導數證明不等式的幾種策略

☉江蘇省常熟市滸浦高級中學 劉健玲

利用導數證明不等式的幾種策略

☉江蘇省常熟市滸浦高級中學 劉健玲

近年來，導數中的不等式證明問題在各地高考題中頻頻出現，這類問題往往難度較大，解題方法靈活多變，對學生的思維能力要求較高.如何利用導數證明不等式？筆者通過平時的教學實踐，談談處理不等式證明的一些方法.

策略一、構造函數求最值來證明

近幾年，函數、導數、不等式的綜合問題是高考中的一個重點，也是一個難點和熱點問題，學生往往對其束手無策.我們可以從不等式的結構特征出發，構造函數，通過求導研究，證明不等式.

例1 已知函數g（x）=lnx+ax2+bx，函數g（x）的圖像在點（1，g（1））處的切線平行于x軸.

（1）用a表示b；

（2）試討論函數g（x）的單調性；

（3）證明：對任意n∈N*，都有成立.

解：（1）b=-2a-1（.2）略.

（3）分析：由于定義域的特殊性，可以將此不等式右端視為一個數列｛an｝（an≥0，n∈N*）的前n項和，若將左端也視為一個正項數列｛bn｝的前n項和Sn，則只需證bn＞an（n∈N*），從而尋求出解題方向.

因為Sn=ln（n+1），所以當n≥2時，Sn-1=lnn，

當n=1時，b1=S1=ln2滿足上式，

即證lnx＞-x2+3x-2，x＞1，

只需證lnx+x2-3x＞-2，x＞1.

由（2）知，當a=1時，函數g（x）=lnx+x2-3x在（1，+∞）上單調遞增，

所以g（x）=lnx+x2-3x＞g（1）=-2，

所以lnx+x2-3x＞-2在x∈（1，+∞）上成立.

故問題得證.

證明：由（2）單調性的證明可知，當a=1時，函數g（x）=lnx+x2-3x在（1，+∞）上單調遞增，

所以g（x）=lnx+x2-3x＞g（1）=-2，即lnx＞-x2+3x-2.

（1）若?x∈［1，+∞），（fx）≤m（x-1）恒成立，求m的取值范圍；

（2）分析：類似例1中不等式的證明思路，不妨將此不等式右端視為一個數列｛an｝（an≥0，n∈N*） 的前n項和，若將左端也視為一個正項數列｛bn｝的前n項和Sn，那么要證這個復雜的不等式，就只需證bn＜a（nn∈N*），從而尋求出解題方向.

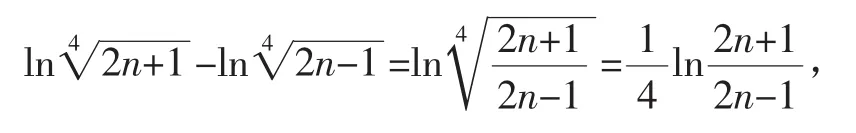
要證原不等式成立，

令k=1，2，3，…，n，得如下n個不等式：

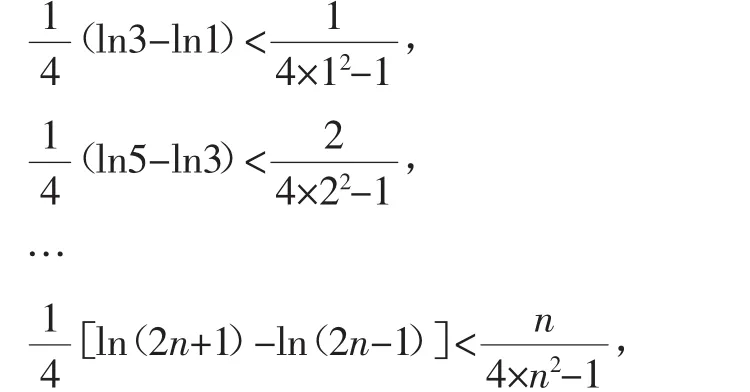
（1）若（fx）無極值點，求a的取值范圍；

解：（1）（2）略.

（3）分析：類似上兩個例題中不等式的證明思路，不妨將此不等式左端視為一個數列｛an｝（an≥0，n∈N*）的前n項和，若將右端也視為一個正項數列｛bn｝的前n項和Sn，那么要證這個復雜的不等式，就只需證an＞b（nn∈N*），從而尋求出解題方向.

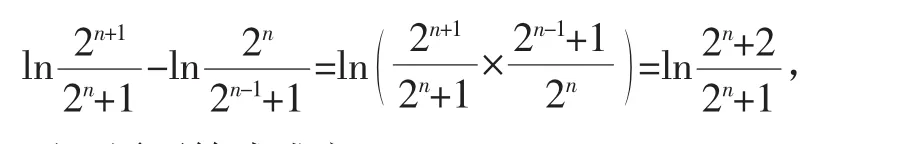
要證原不等式成立，

觀察（*）式，左邊含有2n與2n+1，考慮到

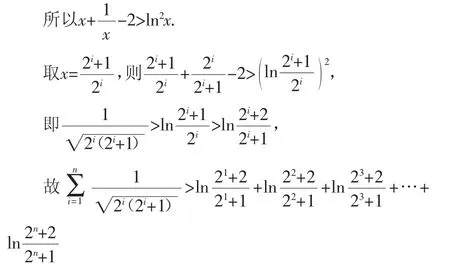
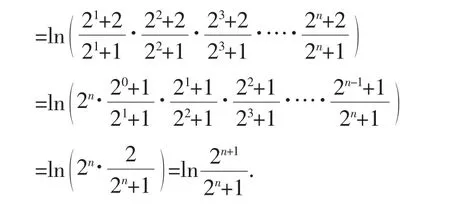
故結論成立.

構造函數證明不等式，要構造可導函數，利用導數得到函數的性質，再利用性質得出不等關系.

策略二、利用導數結合恒成立的思想證明

（1）求a，b；

（2）證明：（fx）＞1.

解：（1）a=1，b=2（.過程略）

設函數g（x）=xlnx，則g（′x）=1+lnx，

故h（x）在（0，1）單調遞增，在（1，+∞）單調遞減，從而h（x）在（0，+∞）的最大值為即（當且僅當x=1時取等號）.

本題在證明（fx）＞1時，學生會想到直接求出（fx）的最小值，再證明（fx）min＞1，或構造函數F（x）=（fx）-1，再證明F（x）min＞0.但這些解法都無法求出導函數零點，進而促進我們思考是由于exlnx引起，故想到將其分離，轉化成然后再加強為（fx）min＞g（x）max進行證明，從而得到上面的證法.

策略三、利用導數結合放縮法證明不等式

有些題型，即使對函數變形后仍然很難找到解題的突破口，有時就有必要利用放縮法對原函數進行放縮.

（1）求a，b的值；

解：（1）a=0，b=-1（.過程略）

（2）由基本不等式，當x＞0時，

令g（x）=（x+6）3-216（x+1），則當0＜x＜2時，g′（x）=3（x+6）2-216＜0，因此g（x）在（0，2）內是減函數.

又由g（0）=0，得g（x）＜0，所以h（′x）＜0，

因此h（x）在（0，2）內是減函數.

總之，導數是解決數學問題的有力工具，不等式也是高考中的重點和難點，兩者結合起來可以使得問題的解決簡單便捷.因此在平時的教學中要多總結，多反思，長期以往，必將收到良好的利益.