例談小學數學教學中的接受學習和發現學習
周杰
【摘要】本文論述接受學習和發現學習兩種不同的學習方式,它們并非是非此即彼的選擇,而應在教學中有效并存,實現有意義的學習,教師可根據教情和學情靈活選擇運用,有機整合,提高學生學習效率。
【關鍵詞】接受學習 發現學習 有效并存 靈活選擇 有機整合
【中圖分類號】G 【文獻標識碼】A
【文章編號】0450-9889(2018)11A-0055-02
美國教育心理學家奧蘇伯爾將學習分為接受學習和發現學習兩種。接受學習,主要是通過老師呈現的材料來掌握現成知識的學習方式;發現學習,則是由學生自主發現問題并解決問題的學習方式。
新課程標準倡導自主、合作、探究,但并不排斥接受學習。然而,在現實中不少教師總是傾向于否定接受式學習,把接受式學習等同于機械學習,等同于講授和被動學習,認為接受式學習不利于學生的能力發展。其實,接受式學習是人類認識世界的基本學習方式,有助于學生理性思維的培養,有助于學生基礎能力的發展。筆者認為,這兩種不同的學習方式,在教學中并非一定要做出非此即彼的選擇,而應在教學中有效并存,靈活選擇,有機整合。
一、有效并存,實現有意義的學習
奧蘇伯爾指出:接受學習未必是機械學習,發現學習也未必是有意義的學習。也就是說,無論是接受學習還是發現學習都可能是機械的,也可能是有意義的。他還強調,要使學習有意義,必須具備兩個條件:一是學生能夠表現出將新舊知識之間建立聯系的傾向和愿望;二是學習內容對學生來說具有潛在的意義。有意義的學習不僅受到學生自身因素的影響,也有學習材料的影響。
在實際教學中被誤認為“機械的”接受學習,其根本原因在于教師在教學中未能激發學生的學習興趣,不注意引導學生理解學習材料的意義。數學學習的內容既要激發學生學習的興趣,也要引導學生與已有的認知結構相聯系,才能順利實現知識的同化與順應。
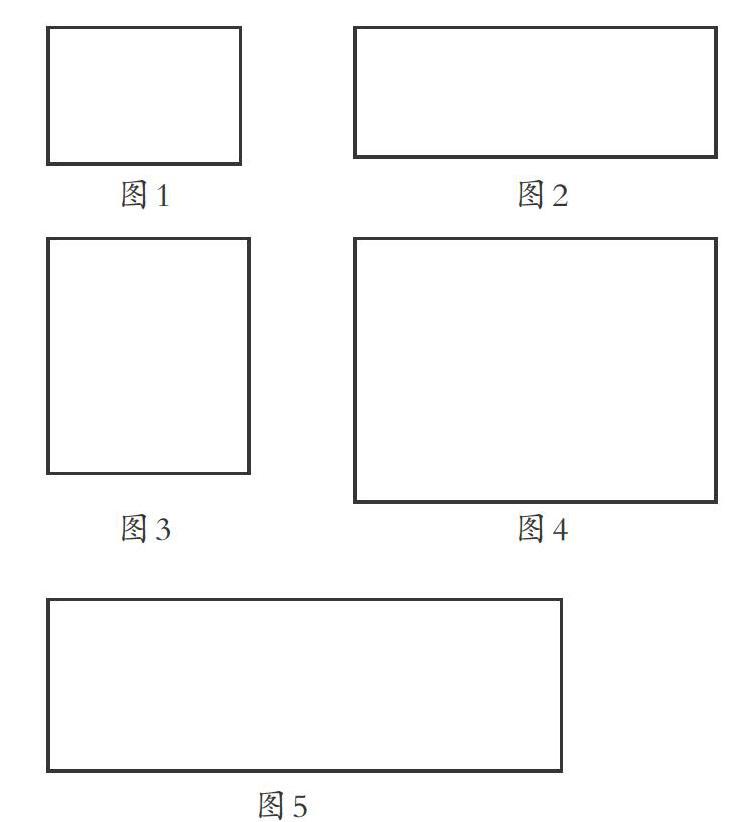
如在教學蘇教版數學六年級下冊《圖形的放大與縮小》時,教師出示一個長4厘米、寬3厘米的長方形(如圖1),然后將圖1的長拉伸,形成圖2,將圖1的寬拉伸形成圖3,再將圖1的長和寬都拉伸形成圖4。
提問:三幅圖中只有一幅圖符合數學意義上的放大。你認為是哪一幅?為什么?
學生通過辨認、思考,認為圖4符合,因為長和寬都要變大。
教師追問:是不是長和寬都變大了,就一定是放大?
出示圖5(將圖1的長拉長,寬也拉長但放大倍數不同),引導學生得出:放大時,長和寬要放大相同的倍數。
(比較有關長度,讓學生說說是怎樣放大的)
教師引導:這是我們用學過的“倍”來表示的,能用比來表示嗎?學生紛紛回答:1∶2,1∶4……
(教師不急于判斷對錯,而是讓學生閱讀、自學課本,圈出認為比較重要的地方)
學生自學后,教師出示文字讓學生輕聲讀一讀:把長方形的每條邊放大到原來的2倍,放大后的長方形與原來長方形對應邊長的比是2∶1,就是把原來的長方形按2∶1放大。
學習上述內容之前,學生對“放大”和“縮小”并不陌生。但日常生活中“放大”是由小變大,“縮小”則是由大變小。基于學情,教師同時呈現圖形的“拉伸”與“放大”,引導學生在比較中認識數學意義上的“放大”,即長方形的長和寬都要放大;接著教師及時呈現反例,促進學生完善對放大的認識,即長方形長邊放大的倍數與寬邊放大的倍數應相等。
在完成對圖形放大的定性認識后,引導學生探討關于放大的定量刻畫。當談到“放大”和“縮小”時,學生容易直觀地認為把原圖邊長擴大2倍是按1∶2放大,或者由面積擴大到原來的4倍也誤認為是按1∶4擴大。而數學上規定把原圖邊長擴大2倍,恰恰是將這個圖形按1∶2放大。當學生得出“按1∶2放大”或“按1∶4放大”的答案后,教師及時引導學生關注矛盾,激發學生對學習材料產生積極的學習心向,進而自主閱讀教材,理解有關圖形放大的數學規定和一般表述。
二、靈活選擇,提升學習效率
小學數學知識主要由一些概念、規則和數學問題組成。其中,由前人給出的規定性的名詞術語等,比較適合接受學習。如認識負數中,負號怎么寫,就需要接受學習。教學時,教師可以先讓學生用自己的方式記錄下問題中的數量:某天南京氣溫(0攝氏度以上)與哈爾濱的氣溫(0攝氏度以下)等。然后讓學生對自己的寫法進行交流,揭示其中表示與正數意義相反的量可以用“–”來表示,這樣便于與別人溝通,此時接受教學就非常有效。
接受學習能引導學生在盡可能短的時間內獲得盡可能多的知識和技能,并不會必然導致學習過程的枯燥。而在現實教學中,有的老師無論什么內容都要讓學生“發現”一番,不考慮具體情況,而是生搬硬套發現學習的模式,因其不具有啟發意義,同樣會導致機械學習。對于一些數學規則,如商不變規律、分數的基本性質、圖形的面積公式、體積公式等,就可以組織學生嘗試發現學習。如果學習的方法、結論等是學生能夠發現的,應盡可能地采用發現學習;如果學習的內容沒有必要學生親自去發現,或不容易被發現,就應采用接受學習。
發現學習需要學生具有相當的知識經驗和一定的思維水平,并不是在兒童發展的任何階段都適用。因此,教師要根據學生的學力水平選擇適合的學習方式。比如小學低年級初次學習“用豎式計算兩位數加兩位數以及乘除法”時,可以采用接受式學習;而到了高年級學習豎式計算“小數加減乘除法”時,則可以采用發現學習。
三、有機整合,尋求“中間地帶”
我們不難發現,從完全的接受學習到獨立的發現學習,他們之間還存在著接受中有發現、發現中有接受的混合學習方式。教學經驗告訴我們,任何極端的行為都是不可取的。因此,教師在教學中要將接受和發現這兩種看似對立的學習方式整合起來,尋求接受學習與發現學習的“中間地帶”,形成教師主導取向的有意義接受學習與學生自主取向的發現學習的平衡和整合。
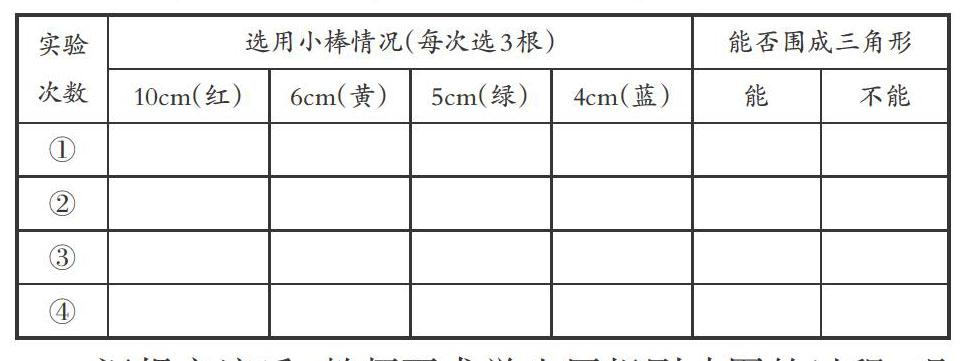
例如在教學蘇教版數學四年級下冊《認識三角形》時,教師拋出問題:給你3根小棒,你能圍成三角形嗎?學生發表各自的想法:有的說能,有的說不能,還有的說可能。這時,教師引導學生小組合作,通過實驗填寫表格。學生分組實驗后,再組織交流匯報。
匯報交流后,教師要求學生回想剛才圍的過程,觀察黑板上的幾組數據,說說有什么發現。
生1:兩條邊合起來比第三條邊長,就能圍成三角形。
生2:圍成三角形時,第一短棒加第二短棒,要比第三根小棒長。
生3:兩條短的加起來,要比最長的長,就能圍成三角形。
師:是這樣嗎?我們一起來看黑板上的數據。
然后,教師和學生共同計算、比較,形成如下板書:
5+6>10? 4+5<10? 4+6>9? ?4+6=10
師:三角形兩條邊長度的和大于第三邊。比較三位同學的發現和教師的表述,有什么不同?有什么聯系?
……
師:第二、三位同學的陳述,強調了是兩條短邊之和大于長邊,這樣我們判斷的水平就更高了。請大家量一量剛才各自所畫三角形三條邊的長度,再算一算,看看兩邊之和是否大于第三邊。
在上述教學流程中,發現學習時,教師注重指導的時機和方法的選擇;接受學習時,教師盡可能注意提高學生學習的積極性。發現學習與接受學習結合在一起,學生的自主構建與教師的價值引領結合在一起,效果顯著。
“再創造”的過程包含了有意義的數學發現,因而能夠激發學生的學習興趣和探究動力,加深學生對數學的體驗。在“再創造”的基礎上的接受,就更容易讓學生理解數學知識的來龍去脈。在現實教學中無論是采用接受學習還是發現學習,教師更應該關注激發學生的學習興趣,讓學生主動地學習,學生才能在已有的知識經驗基礎上實現有意義的學習,提升學習效率。
(責編 林 劍)

