“函”“方”互化,實現高效課堂
——在中考復習中,如何運用函數與方程思想提高解題能力
廣東省東莞市石排中學 鄧沛森
在中考復習課中,提高課堂效率是一個重要環節,而怎樣的數學課堂才是有效、甚至高效的呢?數學高效課堂應具備什么特征?
中考數學知識的考查過程中逐步加強數學思想方法的考查,數學思想方法是數學知識在更高層次上的抽象和概括,它蘊含于數學知識的發生、發展和應用的過程中。而函數與方程的思想方法作為基本的數學思想方法之一,在知識的互相聯系,互相溝通中起到了紐帶作用。抓住數學思想方法,善于迅速調用數學思想方法,更是提高解題能力根本之所在。因此,在復習時要注意體會教材例題、習題以及中考試題中所體現的數學思想和方法,培養用數學思想方法解決問題的意識。在中考復習過程中,“函”“方”互化,提高解題能力,實現高效課堂函數與方程思想共分為兩個方面:函數思想與方程思想。
一、函數思想
函數思想,是拋開所研究對象的非數學特征,抽象其數學特征、利用函數的概念和性質去分析問題、轉化問題和解決問題。方程思想,是從問題的數量關系入手,運用數學語言將問題中的條件轉化為數學模型(方程、不等式、或方程與不等式的混合組),然后通過解方程(組)或不等式(組)來使問題獲解。有時,還實現函數與方程的互相轉化、接軌,使復雜問題簡單化,達到最終解決問題的目的。
1.函數思想解決方程問題
例1 一次函數y=kx+b(k,b為常數,且k不為0)的圖像如圖所示,根據圖像信息可求得關于x的方程kx+b=0的解為__________。
解答:∵一次函數y=kx+b過(2,3),(0,1)點,__________,__________,

∵一次函數y=x+1的圖像與x軸交于(-1,0)點,∴關于x的方程kx+b=0的解為x=-1,故答案為x=-1。
小結:函數解析式的函數值對應方程的根,就是該應函數圖像與x軸交點的橫坐標。
2.函數思想解決不等式問題
例2 如圖,函數y=2x和y=ax+4的圖像相交于A(m,3),則不等式2x<ax+4的解集為______。
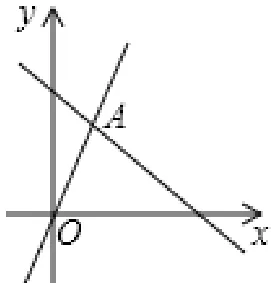
把A(m,3)代入y=2x,得2m=3,解得根據圖像可得:當時,y=2x的圖像在y=ax+4的圖像下方。不等式2x<ax+4的解集是故答案是
小結:判斷函數值大于零還是小于零關鍵看函數圖像在x軸的上方還是下方,上方函數值>0,下方函數值<0。判斷一個函數值大于另一個函數值,看這一個函數圖像是否在另一個函數圖像的上方,在圖像上方函數值大于在下方的圖像的函數值。
3.函數思想解決實際問題
函數思想是有時運用運動和變化的觀點,集合與對應的思想,分析和研究數學問題中的數量關系,建立函數關系或構造函數,運用函數的圖像和性質去分析問題、轉化問題,使復雜問題簡單化,達到最終解決問題的目的。
例3 為改善生態環境,防止水土流失,某村計劃在江漢堤坡種植白楊樹,現甲、乙兩家林場有相同的白楊樹苗可供選擇,其具體銷售方案如下表:
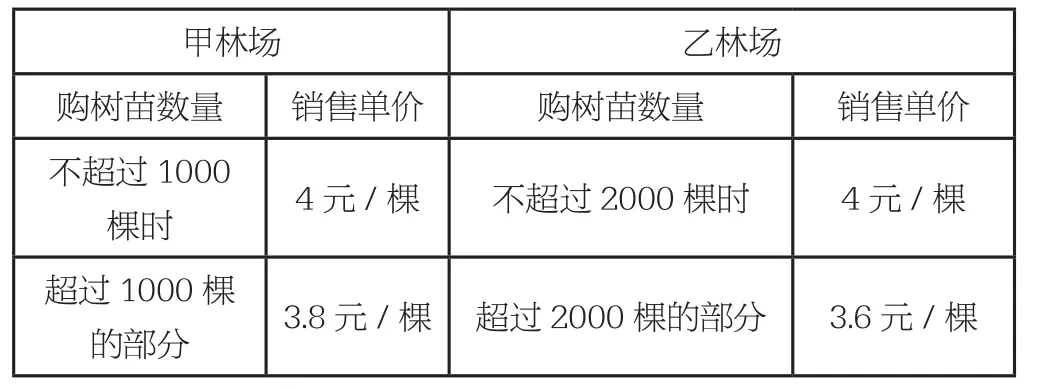
甲林場 乙林場購樹苗數量 銷售單價 購樹苗數量 銷售單價不超過1 0 0 0棵時 4元/棵 不超過2 0 0 0棵時 4元/棵超過1 0 0 0棵的部分 3.8元/棵 超過2 0 0 0棵的部分 3.6元/棵
設購買白楊樹苗x棵,到兩家林場購買所需費用分別為y甲(元)、y乙(元)。(1)該村需要購買1500棵白楊樹苗,若都在甲林場購買所需費用為 元,若都在乙林場購買所需費用為___元;(2)分別求出y甲、y乙與x之間的函數關系式;(3)如果你是該村的負責人,應該選擇到哪家林場購買樹苗合算,為什么?
思路分析:(1)由單價×數量就可以得出購買樹苗需要的費用;(2)根據分段函數的表示法,分別當0≤x≤1000,或1000<x≤2000,或x>2000,由單價×數量就可以得出購買樹苗需要的費用,表示出y甲、y乙與x之間的函數關系式;(3)分類討論,當0≤x≤1000,1000<x≤2000時,x>2000時,表示出y甲、y乙的關系式,就可以求出結論。
小結:用函數思想解決問題,在近幾年中考中占有很大比重,許多省市的中考題都有這部分內容,尤其是用函數的觀點看待方程(組)、不等式和幾何知識等,利用函數解決實際問題,題型多樣化,填空、選擇、解答、綜合題都有,主要考查學生應用函數知識分析、解決問題的能力,所以,實現“函”“方”互化,提高學生解題能力,實現高效課堂。
二、方程思想
方程思想是根據實際問題——數學問題——代數問題——方程問題,在數學的世界里,到處都是等式和不等式。哪里有等式,哪里就有方程;哪里有公式,哪里就有方程;求值問題是通過解方程來實現的……不等式問題也與方程是相近的且密切相關。函數的研究離不開方程研究.列方程、解方程和研究方程的特性,都是應用方程思想時需要重點研究的。
1.數與式中的方程思想
用方程思想解題的關鍵是利用已知條件或公式、定理中的已知結論構造方程組。
例4 如果單項式 -3x4a-by2與x3ya+b是同類項,那么這兩個單項式的積是( )
A.x6y4; B.-x3y2; C.x3y2; D.-x6y4
本題通過同類項的相關定義,構造出方程組。
2.方程思想解決函數問題
兩個一次函數圖像的交點表示點在兩條直線上的橫坐標相同,縱坐標也相同。例如:求直線y=x與y=3x-4的交點,就可以把兩個二元一次方程組成方程組解得所以兩條直線的交點坐標為(2,2),那么我們也可以在坐標系內畫出這兩條直線的圖像,如右圖所示,觀察兩條直線的交點,正是(2,2)。
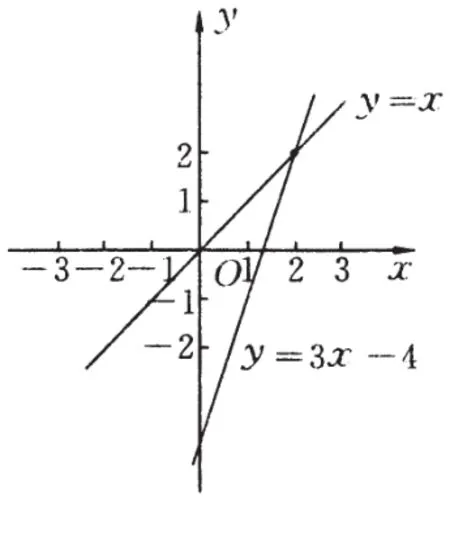
小結:兩個函數圖像的交點坐標就是對應函數解析式所組成的方程組的解。反過來,組成的方程組的解就是兩個函數圖像的交點坐標。
3.平面幾何中的方程思想
例5 如圖,正方形紙片ABCD的邊長為3,點E、F分別在邊BC、CD上,將AB、AD分別沿AE、AF折疊,點B、D恰好都落在點G處,已知BE=1,則EF的長為_____。
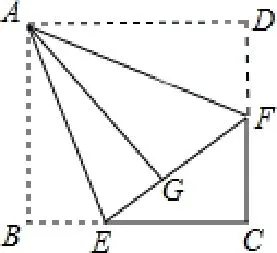
解:∵正方形紙片ABCD的邊長為3,∴∠C=90°,BC=CD=3,根據折疊的性質得:EG=BE=1,GF=DF,設DF=x,則EF=EG+GF=1+x,FC=DC-DF=3-x,EC=BC-BE=3-1=2,在Rt△EFC中,EF2=EC2+FC2,即(x+1)2=22+(3-x)2,解得故答案為
評論:通過正方形、折疊相關的定理與性質,將平面幾何問題,轉化為方程思想問題。
小結:方程思想就是把問題中的已知量與未知量之間的數量關系,運用數學符號語言轉化為方程(組)或其他形式的數學模型,使問題得到解決的思想方法。
(1)把問題歸結為確定一個或幾個未知數;
(2)挖掘問題中已知與未知數量之間的等量關系,建立方程或方程組;
(3)求解或討論所得方程或方程組;
(4)檢驗并作出符合問題實際的回答。
方程的思想方法就是從問題的數量關系分析入手, 運用數學語言將問題中的條件轉化為數學模型,然后通過解方程使問題獲解。
函數研究是數學的主線,它用聯系和運動、變化的觀點研究、描述客觀世界中相互關聯的量之間的依存關系,形成變量數學的一大重要基礎和分支。函數思想以函數知識做基石,用運動變化的觀點分析和研究數學對象間的數量關系,使函數知識的應用得到極大的擴展,豐富并優化了數學解題活動,給數學解題帶來一股很強的創新能力。
函數思想與方程思想的聯用。在解綜合題中,解決一個問題常常不止需要一種數學思想,而是兩種數學思想方法的綜合運用.例如函數思想與方程思想的綜合運用,它們之間的相互轉換一步步使問題獲得解決,轉換的途徑為函數——方程——函數或方程——函數——方程等。所以實現“函”“方”互化,大大提高學生解題能力,實現高效課堂。

