質樸揚新 開放統一 立意能力
——對一道中考壓軸題的賞析

☉安徽安慶市宜秀區五橫初級中學 戴向陽

（2017·安徽第23題）已知正方形ABCD，點M為邊AB的中點.

（1）如圖1，點G為線段CM上一點，且∠AGB＝90°，延長AG、BG分別與邊BC、CD交于點E、F.

①求證：BE=CF；

②求證：BE2=BC·CE.

（2）如圖2，在邊BC上取一點E，滿足BE2=BC·CE，連接AE交CM于點G，連接BG并延長交CD于點F，求tan∠CBF的值.

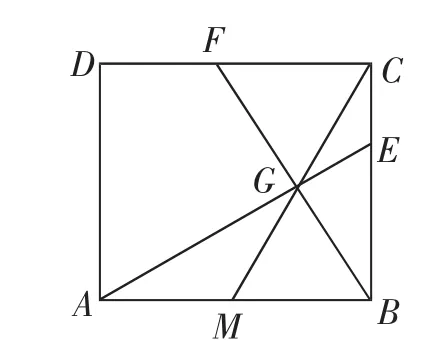
圖1

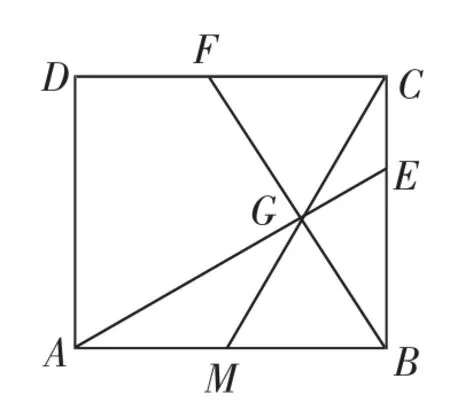
圖2

二、特色解讀

本題源于教材，低起點，高輸出；解法多樣，爭奇斗艷；問題梯度分明，由易到難，思維水平逐級提高，使不同能力水平的學生到達問題的不同深度，體現了新課標關于義務教育階段的培養目標的基本理念：“要面向全體學生，適應學生個性發展的需要，使得人人都能獲得良好的數學教育，不同的人在數學上得到不同的發展.”

1.立題質樸，揚于創新，試題設計凸顯了習題改編之道.

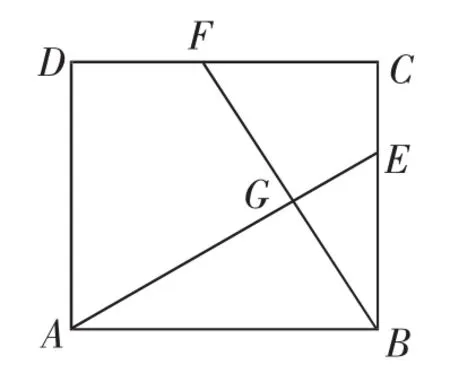
圖3

本題取材于滬科版《義務教育教科書·數學》八年級下冊第104頁第9題：“如圖3，在正方形ABCD中，點E、F是邊BC、CD上的點，且BE=CF.那么，線段AE與BF的夾角有多大？為什么？”命題人別出心裁，巧妙地在此題中融合了新元素——“黃金分割”（滬科版《義務教育教科書·數學》九年級上冊第68頁例3），有效地將典型習題、教材例題同教材閱讀與欣賞整合起來，借雞生蛋，不愧是命題改編的典范之作.

本考題從逆命題角度對原題做了改造，得到第（1）①問.于考生而言，素材是熟悉的、親切的，難點低，較之圖3，圖1只不過多了干擾“直觀”的線條——CM.較之新定義問題，它沒有因陌生符號或概念帶來的壓抑感，也沒有因“定義”的新穎，給人興奮與短暫的沖動.試題入口平淡如茶，考生對壓軸題的畏難情緒得以釋放，在心理上樹立了答對問題的信心.考題起點低，平實無華，中、下水平的學生也易獲得“成功感”.如果命題僅止于這點質樸，作為整卷壓軸便失去了價值.命題者是烹飪高手，稍加“作料”——點M為邊AB的中點，又燒出一道膾炙人口的考題（1）②.如此揚起了壓軸題的層次，有效甄別了中等以上學生.然而考題似意猶未盡，對（1）②放寬條件，再拔新高，去掉中點M，逆向思考，遂成問題（2），試題難度再次“高溫發酵”，至此，考題對“學優生”與“中等生”具有了鮮明的區分度，拉大了不同能力考生的考分差距，試題的甄別功能豁然明朗.本道考題的命制過程，正好彰顯了幾何試題改編與創新的途徑：立于課本典型習題，或強化條件，或弱化條件，或逆向思考，或挖掘一般性，或駐足特殊性，或整合例題和習題，或伸向教材閱讀材料.一道好的考題，常常是在質樸中揚新，一道備受青睞的壓軸題，追求的當是低輸入、高輸出.

2.解法開放，千秋統一，在簡練解法的探求中分享函數奇彩.

一道樂于稱道的考題，不但體現在設計上，還表現在解法上既互異又統一.不同方法中有著統一，在統一中障顯著異彩，差異與統一交相輝映.本題解法開放多樣，使不同“學力”的人，能立足于自身的認識結構，形成不同的解法.對于第（1）①問，解題入口明朗，考生的解法主體上都統一在尋求△ABE≌△BCF上.不同之處，在證角的途徑上略有差異，限于篇幅這里不再一一羅列.對于第（1）②問，解題入口比較隱蔽，但解法也主要在集中統一于證明△CGE∽△CBG，只是在尋找角相等的細節上與CG=BE時略顯千秋，至于其他方法大同小異，不過繞得很，這里亦不再例舉.對于問題（2），中考參考答案給出了兩種差異顯著的解答，鑒于過于復雜，本文也不再贅述.筆者不滿于參考答案的煩瑣，經過一番探索，分別從幾何和代數角度找到兩種相對簡練的解法，在此以饗讀者，分享函數奇彩，不當之處希不吝賜教.

解法1：如圖4，過M點作MN∥BC，則有△CGE∽△MGN，所以

因為BE2=BC·CE，所以

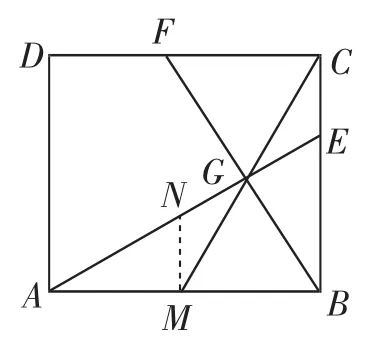
圖4

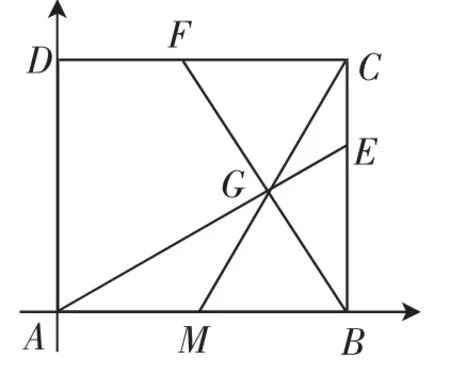
圖5

由BE2=BC·CE，知E是BC的“黃金分割點”，從而即tan

解法2：令正方形的邊長為1，以AD為y軸、AB為x軸建立平面直角坐標系，如圖5所示.

由BE2=BC·CE，知E是BC的“黃金分割”.又BC=1，所以故E

3.立意能力，彰顯素養，發揮“基本活動經驗”與“幾何直觀”在解題中“指揮棒”的作用.

本題以質樸立題，在“移步換景”與角度變換中創新試題，突出了新課標的要求——“由知識立意向能力立意轉變”.波利亞曾說過：“解題的成功要靠正確思路的選擇，要靠從可以接近它的方向去攻擊堡壘，為了辨別哪一個思路正確，哪一個方向可接近它，就要試探各種方向和思路.”所以每道題的解答，都需要解題者在未知情形下去探索，從認知結構中的“基本活動經驗”出發，尋求解題思路，發揮好“基本活動經驗”與“幾何直觀”在解題中“指揮棒”的作用.

解題能力是在親身的實踐中潛移默化形成的.學生的能力起于“基本活動經驗”，行于“數學直觀”，成于分析和推理，熟于思維方式，收于基本思想.對于第（1）①問，證線段相等，想到三角形全等，去尋找全等的條件，這是解決線段相等的“基本活動經驗”之一.再如求證BE2=BC·CE，“基本活動經驗”有：把乘積式化成比例式，尋求三角形相似，以及用等量線段替換，在問題串中前一問往往對后一問具有“墊腳磚”的作用；在探索相似過程中，必要時需根據直觀添加輔助線.在“基本活動經驗”的指引下，幾何思考與“幾何直觀”如影相隨，一邊分析一邊推理.如在“基本活動經驗”確定證明△ABE≌△BCF時，“幾何直觀”與分析和推理同棲同飛，證明全等需要什么條件？圖中有嗎？能在推理中抵達目標嗎？同樣對于第（1）②問，證△CGE∽△CBG時，也經歷了相同的追問思考.在經歷了第（1）題兩小問的充分探索與思考后，思維業已成熟，成熟的思維很快意會到第（2）問需要尋找相似，需要添加輔助線.這一思考流程，正是考生能力的再現.解法1是停留在幾何層面的思維方式，是基于中考參考答案的反思與優化；而解法2，在思維方式上是一種突變：從幾何思維方式轉變為代數思維方式，在解題者眼中“線”不再是幾何上的“線段”，而是代數上的函數圖像，這是深層“基本活動經驗”的喚醒.解題之奇，源于“線段”到函數圖像基本經驗的建構，出于思維方式之奇，收于思想方法之變.

本題立意充分體現了《中國學生發展核心素養總體框架》中“科學精神”之素養.

三、教學導向分析

中考題的命制方向對平時教學起著導航與理念轉變的作用.本道試題對數學教學有哪些啟示呢？概括起來，可用四個放眼來描述.

1.放眼教材.

一些好的中考題，多以教材為本，從教材的例題、習題中挖掘演變而來.日常教學中，要理解每一道例題、習題的價值，靈活地對有“曲度”的試題進行變式、拓展或改造，拓寬學生的眼界、拓長思維的深度、延伸認識的統一，從而舉一反三，解一題通一類.

2.放眼課標和核心素養框架.

教學要研讀課標，明重點、清難點，知哪些需深挖、哪些點到為止、哪些需補給、哪些要遠足，把握節奏，需慢就慢.要吃透并理解核心素養框架要求，認真落實六大核心素養.

3.放眼實踐.

能力，是個體在實踐中形成的，教練教游泳，掌握的是寫在書本中的知識，只有下水，才能學會游泳.能力是靠學習實踐中“基本活動經驗”的建構來形成的.解題能力，也只有在解題中構建“基本活動經驗”才能形成.所以數學教學，先讓學生自己學，教師再介入，進行指導糾正.那種先灌輸再練習的做法，缺失的是“基本活動經驗”的建構過程，學會的永遠是模仿和套用.

4.放眼學生.

決定數學能力的關鍵是思維方式和思想開放度.思維迥異、思想開放的人才不會畏首畏尾，不會受慣性綁架，這是創新型人才一個突出的標志.所以教學中，不要過早拋擲結論，不要冷對學生質疑，不要用“理所當然”冷視學生熱情，要善待學生發出的不和諧的聲音，視學生是一個可以共商大計的人.