一道中考函數壓軸題的一題多解賞析

☉湖北武漢市漢鐵初級中學 馮 英

☉湖北武漢二中廣雅中學 李鴻運

近年來，在全國各地中考壓軸題的關鍵一問中，大多涉及二次函數與一次函數問題，本題就拋物線上一“特征點”的求法進行了深入探究，對已知條件中的“兩倍角”問題這一學生感到棘手的難點進行多途徑的突破，歸納出以下八種不同的解決方法，以饗讀者.

問題：如圖1，在平面直角坐標系中，直線與x軸交于點A，與y軸交于點C，拋物線經過A、C兩點，與x軸的另一交點為點B.點D為直線AC上方拋物線上一點，連接CD，使∠DCA=2∠BAC.若存在這樣的點D，求點D的坐標；若不存在，請說明理由.

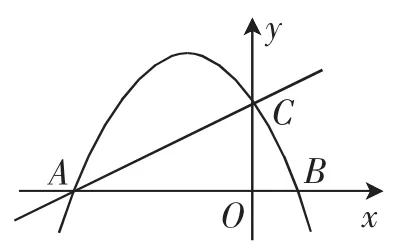
圖1

方法1：如圖2.取AC的中點P，可得P（-2，1），直線OP的解析式為

過C點作DC∥PO交拋物線于點D.

則有：∠DCP=∠CPO=2∠BAC.

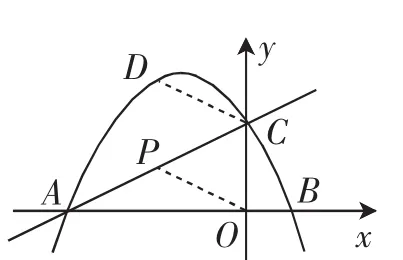
圖2

圖3

方法2：如圖3.取點A關于y軸的對稱點E，則E（4，0），連接EC并延長交拋物線于點D，則∠CAB=∠CEB，∠DCA=2∠CAB.

方法3：如圖4.過C作CH∥x軸，過A作AH⊥x軸，兩線交于H，作A點關于CH的對稱點A′，連接A′C交拋物線于點D，∠A′CH=∠ACH=∠CAO，則∠A′CA=2∠BAC，A′（-4，4）.

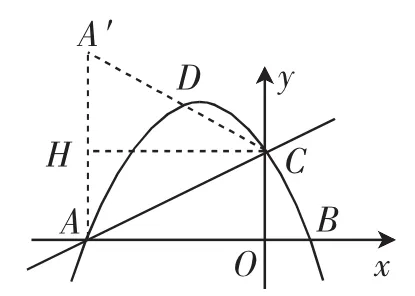
圖4

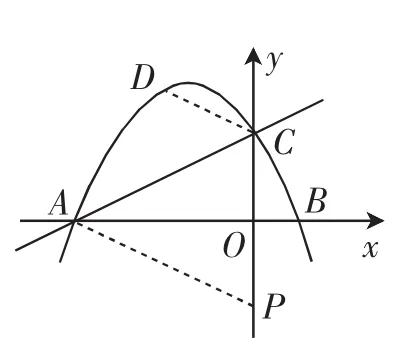
圖5

方法4：如圖5.在y軸的負半軸上取一點P，使OP=OC，則P（0，-2）.連接AP，過C作CD∥AP交拋物線于D，則∠CAP=2∠CAB=∠DCA.

方法5：如圖6.連接BC.由OA=4，OC=2，OB=1，可得∠ACB=90°，取AB的中點M.

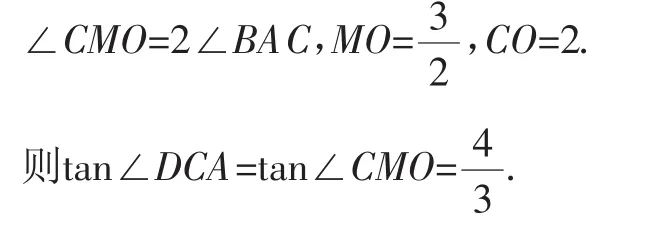
過A作AP⊥AC交CD的延長線于P，過P作PH⊥x軸于H.

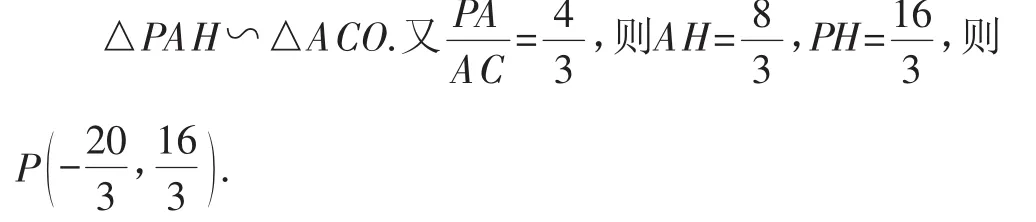
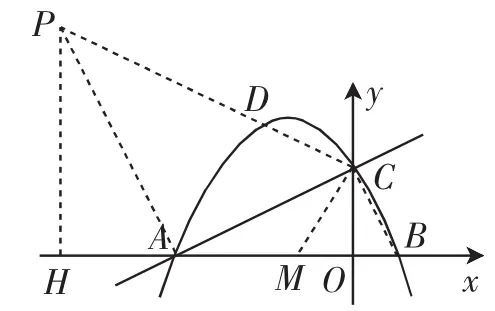
圖6

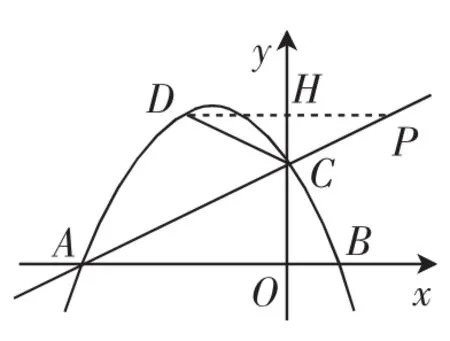
圖7

求得D（-2，3）.

方法6：如圖7.過D作DH⊥y軸于H，并延長交AC于P.

則∠DPC=∠CAB.

當∠DCA=2∠CAB時，有∠DPC=∠PDC，則tan∠PDC=

設CH=a，則D（-2a，a+2）.

方法7：如圖8.過D作DM⊥x軸于M，交AC于G；過C作CH⊥DM于H.

∠DCA=2∠BAC，∠HCA=∠BAC，則∠DCH=∠ACH，則D、G關于CH對稱.解得m1=0（舍），m2=-2，則D（-2，3）.

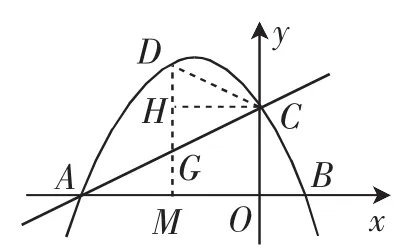
圖8

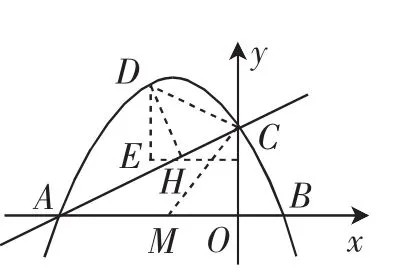
圖9

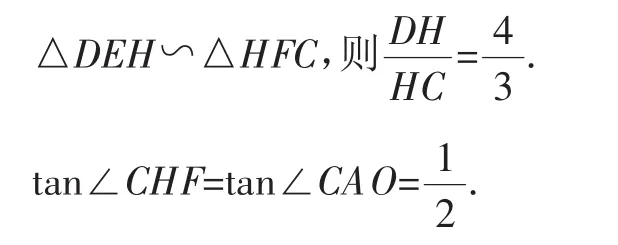
設CF=3a，則HF=6a，EH=4a，DE=8a，則D（-10a，2+

點評：在拋物線上求一個點的方法往往是由題意先求出過該點所在直線的解析式，再和拋物線方程聯立，得到該點的坐標.以上8種方法中，方法1至5都是這一思想，不同之處是直線CD的構造方法不同，或者說直線CD上的“特征點”的選擇不同而產生了5種不同的求特征直線的方法.方法6至8則是由邊角關系得到點D的坐標，再代入拋物線的解析式中，從而求得D點的坐標.三角形相似和三角函數都用上了，各有特色，匠心獨運，值得讀者仔細琢磨、體會.有創造性的解法歡迎讀者交流.