構造全等，柳暗花明

沈善珍

[摘? 要] “授之以漁”在素質教育背景下的詮釋，不僅僅是教會學生怎樣捕魚，還要啟發學生自主發現捕不到魚的原因，以及捕不到大魚的原因，從而引發學生進一步實踐與思考.

[關鍵詞] 初中數學;方法;思想;價值

全等三角形是初中數學幾何中重要的基礎知識，利用全等三角形的相關性質解決與之相關的幾何問題是常見的解題思路. 在幾何問題中，有些全等三角形在圖形中會直接呈現，而有些全等三角形則比較隱蔽，或找不到“現成”的，需要我們自己去“構造”. 對于這類問題，添加輔助線是必要的，但學生往往對如何作輔助線感到困難，相應的問題得分率較低. 如何根據題目所給的條件作出相應的輔助線，構造出全等三角形，對幾何問題的解決具有決定性作用. 本文結合實例，談談構造全等三角形的幾種輔助線添加方法，以期給各位讀者提供參考.

倍長線段法

倍長就是針對性地將線段延長至原來的2倍，這是求解與線段長度有關的幾何問題的常用方法. 通過倍長，可以得到相等的線段，從而為全等的證明提供所需的條件.

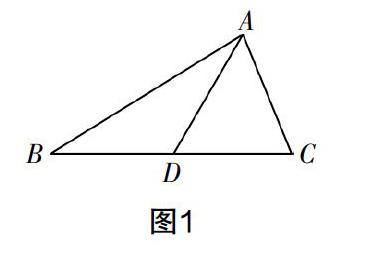
例1 如圖1，在△ABC中，AB=5，AC=3，求中線AD的取值范圍.

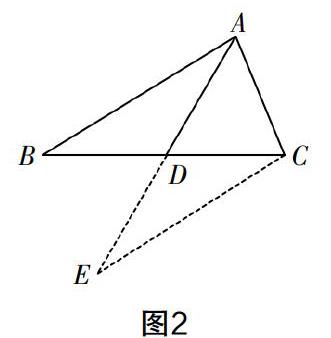
分析 看到求線段的取值范圍，我們往往會聯想到三角形的三邊關系，于是如何將圖中的AD轉變成三角形的邊是解決該問題的關鍵. 由中線的定義可知D是BC的中點，因此可倍長AD（如圖2）得ED=AD，然后根據“SAS”證出△ABD≌△ECD，從而將得到CE=AB=5. 根據三角形三邊的關系可知EC-AC<AE<EC+AC，即5-3<2AD<5+3. 所以1<AD<4.

中線、中點往往是倍長線段的“提示”，如果已知條件中存在線段的中點或三角形的中線，可通過倍長線段作為輔助線，構造相等線段，證明三角形全等. 倍長線段除了可以得到全等三角形外，有時還可以構造出平行四邊形，如倍長三角形的中線，為相關問題的解決提供條件.

截長補短法

截長補短法是在較長的線段中截取一條線段等于已知線段或延長較短的線段使之與較長的線段相等的作圖法. 它雖包括“截長”和“補短”兩種方法，但這兩種方法的實質是相通的，都是將長度不等的線段轉化為長度相等的線段. 通過“截長補短”得到相等的線段，可以為兩個三角形的全等提供所需的條件.

例2 如圖3，在四邊形ABCD中，BC>BA，AD=CD，BD平分∠ABC. 求證：∠A+∠C=180°.

分析 試題要證兩個角之和是180°，應與三角形的內角和有關，因此需要將角進行轉化，而通過全等三角形的對應角來實現角的轉化是常用的方法. 題中所給的條件已具備公共邊BD與一組角（即∠ABD=∠CBD），所以只需在BC上截取BE=AB即可（如圖4）. 于是可證得△ABD≌△EBD，則有∠BED=∠A，AD=ED. 由條件AD=CD可得ED=CD，于是有∠C=∠DEC. 再由∠BED+∠DEC=180°得到∠A+∠C=180°.

上述方法屬于“補短”，該問題也可以通過延長線段BA使之與BC相等來解決.

截長補短法是解決線段和差問題的重要方法，也是將不等線段轉化為相等線段的方法，實質是轉化思想. 通過轉化得到的相等線段，能為三角形的全等提供重要的條件. 通常，在幾何問題中，存在兩個三角形中有一條邊、一個角相等時，便可以用截長補短法來實現另外一條邊相等，從而得到全等三角形.

作平行線法

平行線因其特殊性，其性質通常被作為解決幾何問題的重要依據. 平行線在幾何問題中的作用常常是提供角與角之間的關系，而角正是三角形全等的重要元素. 通過作平行線得到相等的角，也是構造全等三角形的一種方法.

例3 如圖5，點D在等邊三角形ABC的邊AB上，點F在邊AC上，連接DF并延長交BC的延長線于點E，EF=FD. 求證：AD=CE.

分析？搖 要證AD與CE相等，可以考慮通過三角形全等來實現. 顯然，圖中現成的兩個三角形不全等，所以需要進一步構造. △ABC是等邊三角形這一條件可以給輔助線的添加提供“啟示”——過點D作BC的平行線，仍然可以得到一個等邊三角形ADG（如圖6），從而將AD轉化為DG，通過證明△FDG≌△FEC得到DG=CE，從而得到AD=CE.

幾何問題中線段相等的證明可籠統地分為兩種，一種是通過三角形全等來證明，一種是通過特殊幾何體的形狀來證明. 在三角形全等中，如何將所要證明的邊轉化成三角形的對應邊是關鍵，而根據已知條件推導應該使用的全等證明方法則是重要的思路. 除了三邊對應相等而外，全等的證明還需要通過邊和角的相等關系來實現，而平行線可以通過線段之間的關系得到角之間的相等關系. 在教學實踐中我們發現，在三角形全等的問題中，構造平行線作為輔助線的方法是我們比較容易忽視的方法，學生更是如此. 因此，在全等的相關問題中，有針對性地練習構造平行線是非常必要的.

平移變換法

在平面內，將一個圖形沿著某個方向移動一定的距離，這樣的圖形運動方式稱為“平移”. 平移是幾何中一種基本的圖形變換，通過平移，可以將圖形移動到相應的位置，為問題的進一步解決提供條件.

例4 如圖7，在△ABC的邊BC上取兩點D，E，且BD=CE，連接AD，AE，求證：AB+AC>AD+AE.

分析 試題要證明的是線段和之間的不等關系，可以將線段進行轉化，利用三角形的三邊關系來解決. 因此，需要將要證的線段盡可能地“靠攏”. 由BD=CE可以平移△AEC，使EC與BD重合，點A落在點F處，FD與AB相交于點H（如圖8）. 由此可知AE=BF，AC=FD. 由圖中新構造出的兩個三角形可知FH+BH>FB，AH+DH>AD，所以FH+BH+AH+DH>FB+AD，即AB+FD>AD+FB，因此AB+AC>AD+AE.

證明線段的不等關系，通常由三角形的三邊關系來實現，而將不在同一個三角形的線段轉化在同一個三角形內是證明的關鍵. 但平移不是隨意的，當題中出現相等且平行或位于同一條直線上的線段時，方可進行平移. 平移是一種只改變圖形的位置而不改變圖形的大小及形狀的變換，其實質是構造了有特殊位置關系的全等三角形. 利用這一特征可以解決較多關于全等的幾何問題.

旋轉變換法

旋轉是在平面內將一個圖形繞著某個點旋轉一定的角度得到一個新圖形的一種變換，旋轉前與旋轉后圖形的形狀和大小完全一樣. 旋轉也是一種常見的變換方式，在幾何問題的解決中，通過旋轉可以進行線段、角、圖形的合并，從而使問題簡化.

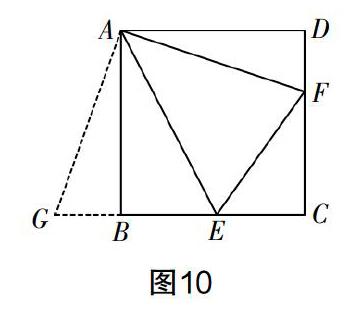
例5 如圖9，在正方形ABCD中，E為BC上一點，F為CD上一點，且BE+DF=EF，求∠EAF的度數.

分析 該問題實際上是“半角問題”. 由BE+DF=EF可知，將△ADF繞著點A旋轉，使得AD與AB重合，得到△ABG（如圖10），于是可將BE與BG“合并”，由“SSS”證得△AGE≌△AFE，因此∠GAE=∠FAE，即∠GAB+∠BAE=∠FAE. 又∠GAB=∠DAF，所以∠DAF+∠BAE=∠EAF. 所以∠EAF=1/2∠BAD=45°.

“半角問題”的常用思路是通過旋轉證三角形全等，從而得到角相等. 該問題是近兩年的熱點問題. 旋轉與平移一樣，是一種全等變換，由于具有可操作性，因此該方法的使用也是對學生動手能力及想象能力的考查. 解題時應根據變換的特征，找到對應的全等形，通過線段、角的轉換達到解題目的.

幾何是初中數學的重要組成部分，作輔助線在幾何問題的解決中起著重要的作用，而構造全等三角形則是解決幾何問題的常見方法. 在三角形全等的構造中，“轉化”是蘊含其中的重要數學思想;通過轉化，構造出全等三角形，再進一步解決問題是基本思路. 輔助線的作法要仔細斟酌題中所給的已知條件與所要求的問題，找到突破口，有的放矢. 當然，與三角形的全等有關的輔助線作法遠遠不止上面幾種，只有深刻挖掘條件，靈活選取方法，才能將問題逐個擊破，使幾何問題“柳暗花明”.