初中數(shù)學(xué)分式化簡求值的技巧總結(jié)分析

江蘇省蘇州市吳江區(qū)蘆墟初級中學(xué) 潘 琪

初中數(shù)學(xué)課程教學(xué)中關(guān)于分式部分的內(nèi)容，是學(xué)生需要重點(diǎn)把握的知識(shí)內(nèi)容，分式化簡求值需要學(xué)生對復(fù)雜的分式進(jìn)行化簡，在結(jié)構(gòu)分析和數(shù)學(xué)關(guān)系的分析中，掌握求值方法和求值技巧。由于初中學(xué)生在分式化簡求值中存在技巧方面的不足，解題效率不高，本篇文章在此基礎(chǔ)上，重點(diǎn)對初中數(shù)學(xué)分式化簡求值的相關(guān)技巧性內(nèi)容進(jìn)行研究與分析，關(guān)于初中數(shù)學(xué)分式化簡求值的幾種有效解題方法和技巧等主要從以下幾個(gè)方面展開研究與探討：

一、去分母計(jì)算

分式化簡求值的過程中需要對結(jié)構(gòu)形式較為復(fù)雜的分式進(jìn)行化簡，對分式中的分母部分進(jìn)行通分、約分，化簡轉(zhuǎn)化為整式，更加有利于簡便運(yùn)算。

在這道題的解答中，需要先對分式進(jìn)行觀察，由于等式兩邊的分式分母不同，分別為（x+1）和（3x+3），要方便分式運(yùn)算，可以將（3x+3）化簡為3（x+1）。左邊分式的分子、分母分別乘以3，分子部分為3x，分母部分同右邊分式分母部分，即為3（x+1），右邊分式部分的分子部分為2x，常數(shù)項(xiàng)部分化為分式形式，分子、分母均為3（x+1），則分式進(jìn)一步化簡為3x=2x+3（x+1），即可進(jìn)入下一步的問題解答。去分母的分式化簡方法在分式計(jì)算中的應(yīng)用較為常見，將分式化簡為整式形式，計(jì)算更加簡便，并且也不會(huì)產(chǎn)生丟項(xiàng)、漏項(xiàng)等問題，但是在此過程中，需要注意分式去分母的過程中，需要分子和分母均同時(shí)除以或乘以某個(gè)數(shù)或某個(gè)項(xiàng)，否則會(huì)影響最終的計(jì)算結(jié)果。

二、合并同類項(xiàng)計(jì)算

分式化簡求值中使用合并同類項(xiàng)的方法，也能夠簡化運(yùn)算過程，合并同類項(xiàng)是根據(jù)乘法運(yùn)算中的乘法分配律，對于同類項(xiàng)的系數(shù)部分進(jìn)行相加，然后將得到的結(jié)果部分作為系數(shù)，但是指數(shù)部分和字母部分仍舊不變。合并同類項(xiàng)在分式化解求值中的應(yīng)用屬于乘法分配律的一種逆運(yùn)算，例如：3a，2a和5a均屬于同類項(xiàng)，a2和-5a2、-ab2和4ab2也是同類項(xiàng)，所有的常數(shù)也都是同類項(xiàng)，合并同類項(xiàng)在分式化簡求值中運(yùn)用可以將相同的項(xiàng)合并，減少項(xiàng)數(shù)，簡化分式結(jié)構(gòu)，使分式計(jì)算更加簡便。

由于這道題中含有四個(gè)不同的分式參與加減運(yùn)算，直接對其通分，化成同分母的分式相加減，考慮到公分母的復(fù)雜度較高，可以把前兩個(gè)分式先相加，在通分運(yùn)算中對同類項(xiàng)部分進(jìn)行合并，即可完成題目的解答。具體的解答過程如下：

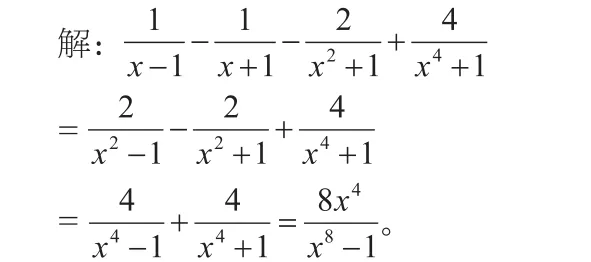
在這道題的解答中，對于前兩項(xiàng)分式，分母部分分別為x-1和x+1，兩邊可以化為（x-1）（x+1）=x2-1，先完成運(yùn)算，然后對于后面的分式部分也可以以此類推，分別通分、化簡、運(yùn)算和求值。合并同類項(xiàng)的分式化簡方法也比較常用，但是老師在教學(xué)中需要引導(dǎo)學(xué)生注意每個(gè)項(xiàng)的特點(diǎn)，對其中的常數(shù)項(xiàng)部分和字母項(xiàng)部分均需要觀察仔細(xì)，否則合并的不是同類項(xiàng)，導(dǎo)致最終的解答結(jié)果不正確，同時(shí)，對于移項(xiàng)和合并同類項(xiàng)，要注意正負(fù)號的變化。

三、分式化簡求值的方法技巧總結(jié)

初中數(shù)學(xué)課程教學(xué)中，老師主要是對學(xué)生進(jìn)行基礎(chǔ)知識(shí)教學(xué)，分式部分是數(shù)學(xué)課程中的重要教學(xué)組織部分，學(xué)生需要在分式概念和基本結(jié)構(gòu)形式的了解中，掌握分式化簡求值的有效方法。分式化簡求值是根據(jù)數(shù)學(xué)運(yùn)算方法和定律，對分式進(jìn)行化簡，使運(yùn)算過程更加簡便。分式化簡方法包括去分母化簡和合并同類項(xiàng)化簡，這兩種化簡方法比較常用，分式在化簡后，項(xiàng)數(shù)減少，結(jié)構(gòu)形式一目了然，數(shù)學(xué)關(guān)系更加明確，分式方程的解答也更加簡便，初中學(xué)生在實(shí)際的學(xué)習(xí)中需要注意自我總結(jié)和歸納，加強(qiáng)自主學(xué)習(xí)。

初中階段的數(shù)學(xué)課程教學(xué)對于學(xué)生的數(shù)學(xué)基礎(chǔ)知識(shí)掌握和數(shù)學(xué)能力培養(yǎng)等具有重要的作用，在實(shí)施教育教學(xué)的過程中，對于分式化簡求值的內(nèi)容，需要老師在課堂實(shí)踐中根據(jù)學(xué)生的具體學(xué)習(xí)情況，向?qū)W生進(jìn)行分式化簡求值解題技巧方面的講解。分式化簡求值是對復(fù)雜的分式進(jìn)行化簡，以約分的方法簡化分式結(jié)構(gòu)，分式化簡方法包括去分母化簡、合并同類項(xiàng)化簡，分式化簡后分式的項(xiàng)數(shù)減少，能夠?yàn)榉匠探獯鹛峁┍憷Ｆ渲校シ帜富喎质绞菍Ψ质椒匠踢M(jìn)行“去分母”，將分式方程化簡為整式方程，這也是分式化簡求值的簡要方法之一；而合并同類項(xiàng)化簡分式，則是對分式中的同類項(xiàng)進(jìn)行合并運(yùn)算，屬于分配律的逆運(yùn)算。初中數(shù)學(xué)課程教學(xué)中，老師通過例題講解和分析的形式引導(dǎo)學(xué)生對分式化簡求值的方法和技巧進(jìn)行歸納和總結(jié)，能夠更加有效地提升學(xué)生的運(yùn)算思維轉(zhuǎn)換能力和解題效率。

[1]邵偉．分式化簡求值中的數(shù)學(xué)思想[J]．中學(xué)生數(shù)理化（教與學(xué)），2011（06）．

[2]饒敏．分式的化簡及求值技巧[J]．初中生輔導(dǎo)，2010（11）．

[3]左加亭．分式求值方法多[J]．中學(xué)生數(shù)理化（八年級數(shù)學(xué)）（人教版），2010（01）．

[4]朱家海．分式化簡求值的若干方法與技巧[J]．?dāng)?shù)理化學(xué)習(xí)（初中版），2009（09）．