在小學數學課堂中滲透“有限思想與無限思想”

廣東省清遠連州市連州鎮實驗小學 賴衛輕

我們經常說自己渺小的像一粒沙子，一粒沙子是有限的，沙灘的沙子是無限的，無限的沙子里包含著一粒粒沙子；一滴水、一桶水、一池水是有限的，一片汪洋是無限的，汪洋大海中能取出有限的一滴水、一桶水……茫茫宇宙有無限大，浩浩星際無限多，千百年來，“有限與無限”是一個古老而又常新的永恒哲學問題，有限與無限這兩者間既有區別，又有聯系,而且在一定條件下可以相互轉化。以下就從幾個方面探究如何在數學教學中滲透有限與無限的思想。

一、在概念教學中滲透有限思想和無限思想

數學教學的具體任務之一——數學概念是數學知識體系的“細胞”，是建立數學理論的基礎。正確理解、掌握和運用數學概念是學好數學理論的前提。數學概念的教學是一項非常重要的任務，在數學概念的教學中滲透有限思想和無限思想，數學是思維的科學,概念是思維的細胞,教好概念是教好數學的內在要求。概念教學搞不好,數學課程目標的實現就失去了根基。因此,我們必須重視數學概念的教學。

二、在計算教學中滲透有限思想和無限思想

在計算教學中，我們往往不會直接點明所應用的數學思想方法，但是我們在教學中已經不經意地滲透了遷移、推理、符號化、有限和無限的數學思想。如在教學《能除得盡嗎》這一課時，我出示情境圖：

然后問：“你們從圖中獲得了什么信息？能提出一個數學問題嗎？”生：“蜘蛛3分鐘爬行73米，蝸牛11分鐘爬行9.4米，它們誰爬行得快？”我繼續追問：“如何可以知道它們誰爬行得快？怎樣列式？”學生回答：“可以比較它們的速度。”還有學生答：“蜘蛛的速度可以用73÷3來計算，蝸牛的速度可以用9.4÷11來計算。”

蜘蛛和蝸牛平均每分鐘爬行多少米？

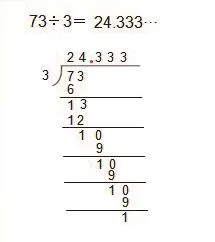
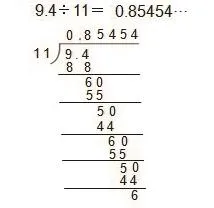
根據展示的學生計算過程，引導學生思考：①通過計算，你發現什么問題？②這兩道題里，商的小數部分和余數有什么特點？③你們如何表示這樣的商？學生小組討論后匯報：“我們發現怎么除也除不盡，73÷3的余數始終是1，商始終是商3，是無限重復。”我再問：“那你們這道題的商的橫式是怎么寫的？為什么寫省略號？小數部分重復出現的數字應寫幾個？”學生回答：“寫省略號表示除不盡；重復數字我們認為寫2個比較合適，因為寫少了，不能表示依次重復出現的特點，寫多了麻煩，也沒有必要。”我再引導學生觀察這兩個商，想一想：這兩道題和我們前面的計算題有什么不同？前面的計算題都能算得完，這兩道題除不盡，這兩道題的商中有數字依次重復出現。最后做出小結：像24.33…、0.85454…等都是無限循環小數。

三、在公式教學中滲透有限思想和無限思想

公式教學在數學教學中非常重要，在公式的教學中經常由抽象到直觀，有數學的模型思想，有轉化的數學思想，還有有限與無限數學思想。如圓的面積，只要給定了一個半徑為定長的圓，無論這個圓的半徑有多大，它的面積總是有限的，在推導面積公式的過程中，通過把圓劃分成無限個全等的扇形，利用這些扇形組成一個近似的長方形，轉化成長方形的面積來計算出面積。

數學思想是數學方法的進一步提煉和概括，數學思想的抽象概括程度高一些，而數學方法的操作性更強一些，所以數學思想方法是數學的靈魂。有限與無限的數學思想除了可以在上述幾種情況中滲透，還有角的邊、平行線、數的認識、直角、平角、周角等數學教學中也可以不斷滲透和提升，數學思想的研究之路艱難崎嶇，需要我們不停摸索探究，我們需要用數學思想的明燈指引數學教學之路走得更遠、更高。