因式分解實錄

廣東省廣州市增城區正果中學 陳強毅

因式分解是初中數學教學與學習的一塊跘腳石，克服它，就能通往更美好的知識甸園。教師在因式分解的教學時也發現，無論怎么教，學生都不會，花很多時間去教學、做練習、復習，但實際效果都不好。學生在學習因式分解時更是著急，越急越學不會，越心慌，有些學生甚至不想往后學習了。有些教師在因式分解的教學時一帶而過，明知教不會，就隨便教。在人教版的因式分解章節中，已經簡化了因式分解的知識點，把十字相乘法放到了選學的內容里，即便簡化了因式分解知識點，只學提公因式法和公式法，學生仍舊難以掌握，這讓很多教師感到困惑。用學生的思維去理解因式分解，去教學，或許會得出意想不到的效果。

一、因式分解的本質

很多學生在學習因式分解時存在困難是因為不明白因式分解的本質和不明白為什么要進行因式分解，因式分解的本質是把一個多項式化成幾個整式的積的形式。因式分解是分式學習的前奏，兩者之間密不可分，息息相關，相互影響。通過因式分解才能約去分式中相同的項，是一個化簡的過程，化簡了才便于運算，讓計算更簡單。在分式通分時，利用因式分解可讓分母變得更簡單，減少錯誤。當學生明白因式分解的意義所在，有目的地進行學習，就會知道學習因式分解是有用的，從而提高學習興趣。因為學生不知道因式分解的用處，又難學，所以大多數學生都不喜歡這個知識點的學習，覺得學來沒用的就不想學了。通過調查了解到學生對因式分解的學習熱情普遍不高，如果學生知道這個知識點是很有用的，那么他們就會加倍努力去學習。有目的，自然效果就不同。

二、因式分解為什么難學

很多老師覺得因式分解的內容簡單，卻不明白為什么學生學起來那么困難。其實，主要有以下幾個原因：

1.提公因式沒學好。

2.公式法沒掌握好。

3.因式分解過于單調，學起來枯燥無味。

4.因式分解和整式的乘法運算是相反的，又十分相似，就像一個沙漏，可以兩邊倒，卻不知哪邊是頭，哪邊是尾。學生在兩者之間的運算是盲目的，沒有方向，什么時候是和，什么時候是積，讓學生很是困惑，不能區分，因而學不好。

5.學生操之過急、不夠耐心，甚至看到因式分解就怕。

三、因式分解在教材中處于一個尷尬的地位

1.因式分解在分式之前，這時學因式分解，學生會覺得枯燥無味，不知道因式分解的用處，一味學習這么困難的知識，一錯再錯，打擊學生學習積極性。學生在和與積之間很難區分，如在代數式2ax2+4ax+2中，和中有積；而在代數式（2x+y）（2x-y）中，積中有和。怎樣才是積的形式，什么時候不能再分解，沒有一個明確的方向，讓學生很是為難，無從下手。

2.如果把因式分解放在分式之后，那么很多約分與通分的知識將無法進行。很多時候，分式的值為0、有意義都與因式分解有關。因此，它只能在分式之前學習。

四、因式分解的方法和步驟

（一）因式分解的方法

在人教版初中數學中，要求學生學習提公因式法與公式法，并在課后閱讀與思考里對十字相乘法進行了簡單的介紹。為了減輕學生的學業負擔，我們主要圍繞這兩種方法進行教學，要求學生盡量掌握這兩種因式分解方法，為以后學習分式等有關內容打好基礎。對于“十字相乘法”，我們只要求學生簡單了解，并介紹一種最簡單的形式——x2+（p+q）x+pq型的因式分解。

1．提公因式法

（1）簡單型多項式因式分解，例如：因式分解8a3b2+12ab3c，在這種形式里，找公因式的順序為先找數字，再找字母。把8寫成2×4，把12寫成3×4，找到數字部分的公因式4，字母部分為ab2。所以，8a3b2+12ab3c的公因式是4ab2。

（2）整體提取型因式分解，例如：因式分解2a（b+c）-3（b+c），這里要把（b+c）看作一個整體進行提取，把剩下的2a-3括起來，結果為(b+c)（2a-3）。

2．公式法

（1）平方差公式法，形式如a2-b2=（a+b）（a-b），它的特征是一般有兩項。

（2）完全平方公式法，形式如a2±2ab+b2=（a±b）2，它的特征是一般有三項。用公式法時必須準確找出代數式中的“a”和“b”。

（二）因式分解的步驟

因式分解的步驟簡記成三個字：1.“提”，即提取公因式；2.“公”，即用公式法進行因式分解；3.“查”，在進行完前兩步后，對結果進行檢查，看看還有沒有可以分解的因式。如：很多學生以為做到這里就完成了，通過檢查，可以發現（a2-b2）還可以分解，正確的做法是

五、因式分解中出現的問題

1．不會加括號

2．很多學生不會把1寫成12

3．提公因式不徹底

4．不會“調位”

在因式分解-4x2+y2時，大部分同學的做法為：-4x2+y2=（-2x）2+y2=（-2x+y）（-2x-y）。-4x2與y2之間是和的關系，卻硬是把平方差公式套上去，說明這部分同學對知識點掌握得不夠透徹。正確的做法應該是先變為y2-4x2，再進行分解，如：-4x2+y2=y2-4x2=y2-(2x)2=(y+2x)（y-2x）。

5．分解不徹底

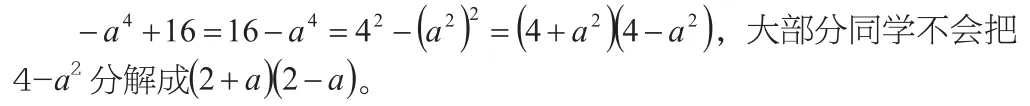
6．不會改變符號

錯例1：因式分解-x2+4xy-4y2=(-x)2+2(-x)·2y-(2y)2=(-x-2y)2，正確的做法是先添負號添括號，再進行因式分解，如：-x2+4xy-4y2=-(x2-4xy+4y2)=-[x2-2·x·2y+(2y)2]=-(x-2y)2。

錯例2：因式分解：m(a-3)+2(3-a)，很多同學在做這道題時不會分解，找不到相同的項，沒有發現a-3與3-a是互為相反數的關系，把m(a-3)+2(3-a)中第二項中的3-a變為a-3，就可以進行因式分解了，方法是把第二項前的“+”變為“-”，即m(a-3)-2(a-3)=(m-2)(a-3)。

7．把符號看錯

8．系數為1時提取漏項

在學習因式分解的過程中，要注意以下幾點：

1.靈活動用公式。

2.會交換加數的位置。

3.會根據公式對代數式進行正確的變形。

4.熟練掌握公式的形狀結構，清楚什么時候能用公式。

六、怎樣能學好因式分解

1.準確地提出公因式，并檢查是否漏項。

2.熟練掌握平方差公式和完全平方公式，方法是每天利用1～2分鐘左右快速讀一遍。

3.用公式法因式分解時，用橫線或方框把公式中的“a”和“b”標記出來。

4.會對代數式進行適當的變形，靈活運用公式。如：-a4+16變形為16-a4，并把a4變為（a2）2。