認清維度、分清測度,輕松破解幾何概型問題
相對于古典概型來說,幾何概型將等可能發生的基本事件的個數從有限推廣到無限。那么幾何概型中常見的測度有哪些呢?下面就從三個方面舉例說明如何認清維度、分清測度,輕松破解幾何概型問題。
一、一維幾何概率模型
測度為長度的幾何概型和測度為角度的幾何概型都涉及一個變量,是一維的,稱為一維模型(或區間模型)。
例1記函數的定義域為D。在區間[-4,5]上隨機取一個數x,則x∈D的概率是____。
分析:幾何概型有兩個特點:一是無限性,二是等可能性。基本事件的構成可以是點,盡管這些點是無限的,但它們所在的區域是有限的,因此可用“比例解法”求解幾何概型的概率。
解:由6+x-x2≥0,即x2-x-6≤0,解得-2≤x≤3。根據幾何概型的概率計算公式,可得x∈D的概率是
例2某地鐵站每隔8min就有一列車到站,假設一位乘客到達車站的時刻是任意的,求該乘客的候車時間不超過5min的概率。
分析:由乘客到達車站的時刻是任意的,可知試驗的結果具有等可能性。
解:由乘客到達車站的時刻是任意的,可知本題屬于幾何概型問題。因為地鐵站每隔8min就有一列車到站,所以總的基本事件所包含的時間長度為8。乘客的候車時間不超過5min的事件包含的時間長度為5。由幾何概型的概率計算公式可得所求概率為
例3如圖1所示,在△A B C中,∠B= 60°,∠C=45°,高在∠B A C內作射線AM交B C于點M,求BM<1的概率。
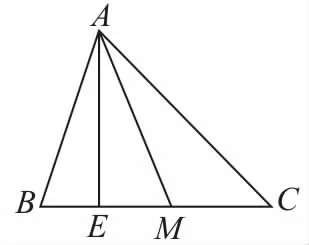
圖1
分析:總的基本事件Ω為“在∠B A C內作射線AM”,事件A為“BM<1”。射線AM在∠B A C內是等可能分布的,當AM與高A E重合時,BM=B E=1,滿足BM<1的射線AM應在∠B A E內,可知測度為一維模型的角度。
解:由于總的基本事件Ω的測度為∠B A C=180°-(60°+45°)=75°,事件A的測度為∠B A E=90°-60°=30°,故所求概率
小結:向區間[a,b]上任意投擲一點,設區間[c,d]?[a,b],則點落在[c,d]內的概率只與區間[c,d]的長度成正比。令Ω=表示試驗的所有可能結果構成的區域表示隨機事件,則所求概率
二、二維幾何概率模型
測度為面積的幾何概型涉及兩個變量,是二維的,稱為二維模型(或平面模型)。有些看似與“幾何”無關的問題,如“取兩數問題”“相遇問題”等,其本質還是幾何概型,且是二維模型。
例4在區間(0,1)內隨機地取兩個數,則兩數之和大于0.5且小于1.5的概率是多少?
分析:本題是在區間(0,1)內隨機地取兩個數,且兩個數是相互獨立的,屬于典型的二維平面問題,測度為面積。
解:設在區間(0,1)內隨機地取的兩個數分別為x,y,則0<x<1,0<y<1,其對應的區域如圖2所示。
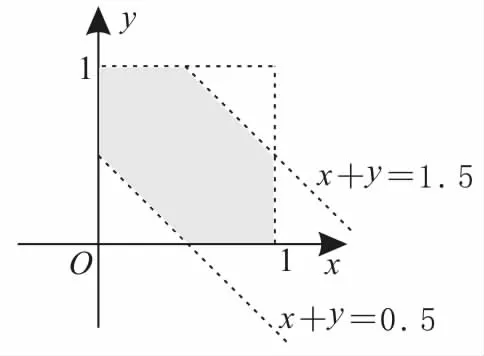
圖2
正方形的面積為Ω=1×1=1。令“兩數之和大于0.5且小于1.5”為事件A,即0.5<x+y<1.5,由此可得陰影部分的面積為S=
例5甲、乙兩人相約8:00至8:30之間到汽車站乘車,這段時間內的8:15和8:30各發一班車。甲、乙兩人在8:00到8:30內任一時刻到達車站都是等可能的。如果先到車站的人見車就上,求兩人能同乘一班車的概率。
分析:(1)分別用x和y表示甲、乙到達車站的時刻,甲、乙兩人在8:00到8:30內任一時刻到達車站都是等可能的。用A表示事件“兩人能同乘一班車”。
解:設分別用x和y表示甲、乙到達車站的時刻,用Ω表示試驗的所有可能結果,則Ω=,如圖3所示。
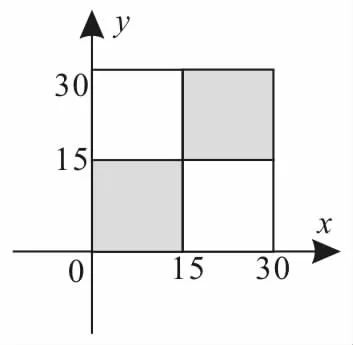
圖3
用A表示事件“兩人能同乘一班車”,則事件A={(x,y)|0≤x≤15,0≤y≤15}∪{(x,y)|15≤x≤30,15≤y≤30}。
小結:向平面區域Ω上任意投擲一點,設隨機事件的平面區域為A,則點落在區域A中的概率只與區域A的面積成正比,而與A的位置和形狀無關。因此所求概率P(“點落在區域A”)
三、三維幾何概率模型
測度為體積的幾何概型稱為三維模型(或空間模型)。
例6如圖4所示,正方形A B C DA1B1C1D1的棱長為1,在正方體內隨機地取一點M,求使四棱錐M-A B C D的體積小于的概率。
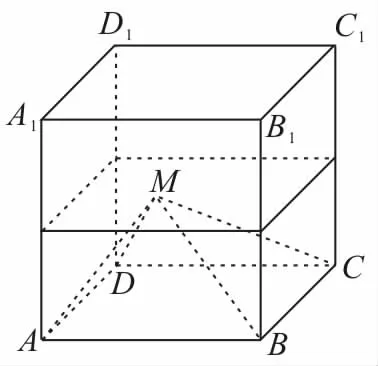
圖4
分析:在正方體內隨機地取一點M,屬于三維模型,測度為體積。
解:設點M到平面A B C D的距離為h。
又因為正方體A B C D-A1B1C1D1的體積為1,所以所求概率為即使四棱錐M-A B C D的體積小于的概率為
小結:向空間區域Ω內任意投擲一點,設隨機事件的空間區域為A,則點落在區域A中的概率只與區域A的體積成正比,而與A的位置和形狀無關。因此所求概率P(“點落在區域A”)
結束語:解決幾何概型問題的關鍵在于弄清題中的考查對象和對象的活動范圍。當考查對象為點且點的活動范圍在線段上時,用長度比(或角度比)計算;當點的活動范圍在平面區域時,用面積比計算;當點的活動范圍在空間區域時,用體積比計算。求解幾何概型問題時,要認清測度,把握所求事件對應的區域,注意與代數、幾何等相關知識的聯系,同時要掌握常見的數學思想方法。

