一題多解話思維 平面向量巧突破

☉安徽省六安第二中學 王立余

思維的廣闊性又稱思維的發散性，是一種不依常規，尋求變異，從多角度、多方位去思考問題、尋求解答的思維品質，它具有流暢、變通、獨創等特征.在解題中，通過捕捉有用的信息，并進行對比、聯想，從一題多解等形式進行練習，這對培養我們思維的廣闊性無疑是有益的.下面就兩道平面向量的高考真題加以一題多解，剖析解題思路，拓展思維品質.

例1（2017年全國卷Ⅱ）已知△ABC是邊長為2的等邊三角形，P為平面ABC內一點，則的最小值是（ ）.

圖1

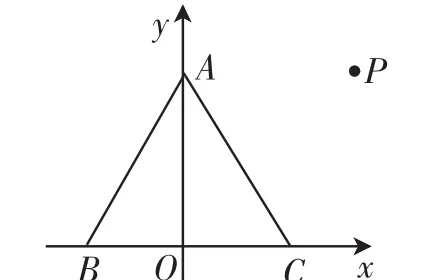
圖2

解題思路4（極化恒等式法）：設BC的中點為D，AD的中點為E，則有P—，當且僅當=0，即P與E重合（P為AD的中點）時，等號成立.

點評：通過以上解法可以發現思路1利用數形結合思想確定點P必須在線段AD上，設出|P—→A|=x，結合數量積公式建立關系式得到對應的二次函數，利用二次函數的配方法來確定最值問題；思路2和思路1一樣先確定點P必須在線段AD上，根據數量積公式并利用基本不等式法來確定最值；思路3通過巧妙構造直角坐標系，利用坐標法來求解相應的平面向量數量積問題，是高考中比較常見的一類技巧策略；思路4是針對特殊關系式下相應恒等式成立時的特殊方法，也是解決數量積問題是一類比較常見的思維方式.

例2（2016年江蘇卷）如圖3，在△ABC中，D是BC的中點，E，F是

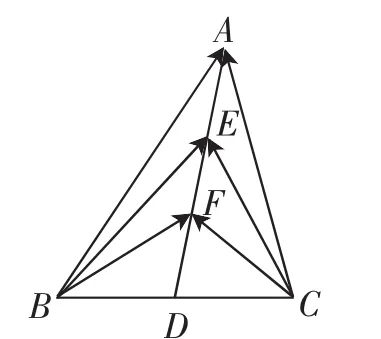
圖3

點評：不難發現思路1和思路2的本質是一樣的，通過不同的向量的數量積或向量的長度作為整體來轉化，金蟬脫殼，達到轉化與求解的目的；同時思路4和思路5的本質也是一樣的，而思路3的基底法只是這兩種解法的一般性應用，同時思路5針對填空題中答案的確定性加以特殊性處理；思路6是針對特殊關系式下相應恒等式成立時的特殊方法.

【總結】涉及平面向量問題，解決中主要體現以下幾個重要的數學解題策略：

1.整體思維，金蟬脫殼，通過代換來轉化與應用，這在解決一些相關的數學問題中經常用到.

2.幾何問題代數化，通過建立平面直角坐標系，利用坐標法來求解相應的向量問題，也是高考中比較常見的一類技巧方法.

3.特殊性思維，通過取一些特殊的值、特殊的點、特殊的位置等，一般問題特殊化，這也是解決選擇題或填空題中比較常見的思維方式.

4.恒等思維，結合常見的恒等式、不等式等直接加以轉化與處理.本題直接采用極化恒等式來轉化，效果非常不錯.

通過一題多解，我們嘗試到：這樣的問題可以使我們的解題思路開闊，妙法頓生，提高了解題速度，培養了發散思維能力，有助于激發我們學習的主動性、積極性、趣味性，從而全面提高我們的知識水平和思維廣闊性.J