再論雙曲線的一個優美性質的簡證與推廣

☉廣西柳州高級中學 林 軍 吳佐慧

☉湖北大學數學系 劉合國

文［1］中的作者提出如下定理：

定理：在雙曲線所在平面內任取一點（該點不在雙曲線和其漸近線上），過此點作兩條漸近線的平行線，這兩條線與雙曲線相交于兩點，與漸近線相交于兩點，則雙曲線上兩點的連線平行于漸近線上兩點的連線.

文［2］從有公共交點曲線系的角度給出該定理的一個簡證，本文將從線性變換的角度給出定理的另一種簡潔證明，并對定理進行推廣.

性質1：線性變換把直線變成直線.

性質2：線性變換把平行直線變成平行直線.

性質3：線性變換保持共線三點的簡單比值不變.

性質4：線性變換把共線的三點變成共線的三點，把不共線的三點變成不共線的三點.

性質5：線性變換把線段變成線段，并保持線段的分比不變.

性質6：線性變換按同一比值改變平面上所有（有面積的）圖形的面積.

在文［4］中，線性變換把圓錐曲線的某些問題簡化成圓或者平面幾何的問題，利用其方程的簡潔性或圓的一些幾何性質，化繁為簡、化難為易，充分體現了化歸的力量.基于這樣的思想，在處理雙曲線的某些問題時，同樣可以用線性變換把雙曲線轉換成等軸雙曲線，使問題得到簡化.

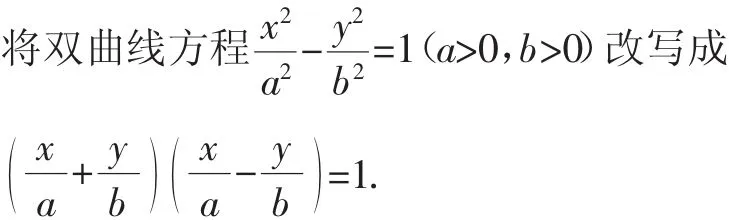
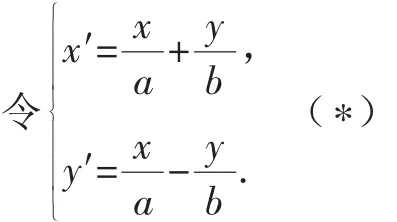
則通過線性變換可將雙曲線變成等軸雙曲線x′y′=1，其漸近線恰為兩坐標軸.線段AB的斜率k變成線段A′B′的斜率k′，且k|AB|，面積

接下來我們給出文［1］定理的證明.證明：將雙曲線用線性變換（*）變成等軸雙曲線x′y′=1，原雙曲線的漸近線變成兩坐標軸（如圖1），設點P（x0，y0） 是不在雙曲線x′y′=1及漸近線上的任一點，過P分別作漸近線的平行線交雙曲線于A、B兩點，交漸近線于E、F兩點，則AE（x，0），F（0，y），直線AB00

由于kEF=kAB，所以AB∥EF.由線性變換的性質2知，在原坐標系下此結論仍成立.

在以上的證明過程中，通過線性變換改變了雙曲線方程的形式，使方程變得更為簡潔，從而達到簡化運算的目的.基于這樣一種思路，我們可得到雙曲線的另外一些有趣的性質.

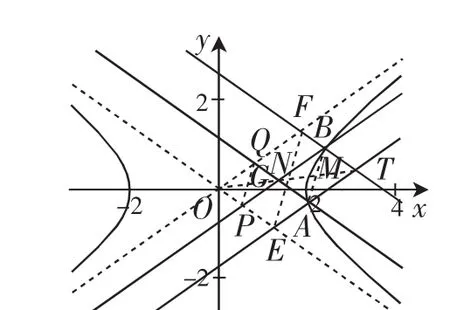
圖2

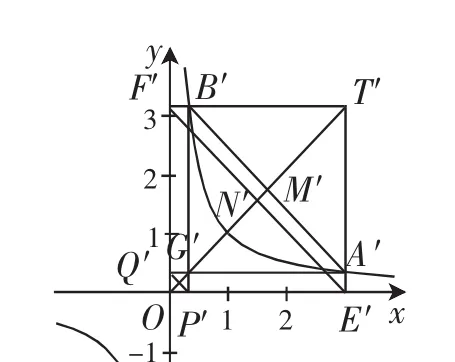
圖3

證明：通過線性變換（*）將雙曲線C變成等軸雙曲線x′y′=1，原雙曲線的漸近線變成兩坐標軸，相應的點變成對應的點，如圖3.設T′（x0，y0），則

又設線段A′B′，E′F′，P′Q′的中點分別為M′，N′，G′，

則各線段的中點與原點O連線的斜率別為

所以kOM′=kON′=kOG′=kOT′，故O，M′，N′，G′，T′五點共線，由線性變換的性質4（線性變換把共線的三點變成共線的三點）知命題成立.

注：（1）由上述證明過程我們可以得到如下結論：過不在雙曲線及漸近線上的任一點P作兩漸近線的平行線交雙曲線于兩點A，B，則直線OP總平分線段AB（O為坐標原點）.

（2）因為kA′B′+kOM′=-0，即是我們得到了文［5］的結論.

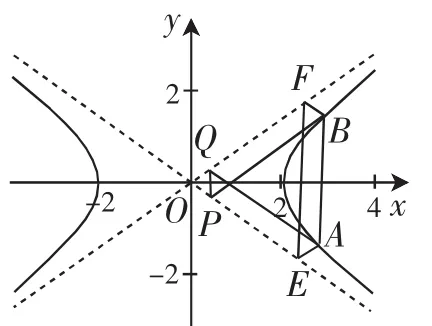
圖4

（1）當A，B在雙曲線的同一支上時，則|AB|=|EF|-|PQ|；

（2）當A，B在分別在雙曲線的兩支上時，則|AB|=|EF|+|PQ|.

證明：通過線性變換（*）將雙曲線C變成等軸雙曲線x′y′=1，原雙曲線的漸近線變成兩坐標軸，相應的點變成對應的點，如圖5.設

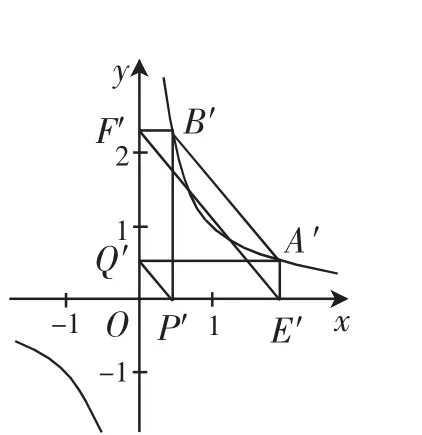
圖5

（1）若點A′，B′在雙曲線的同一支上，不妨設A′，B′均在第一象限的同一支上，且0＜x2＜x1，

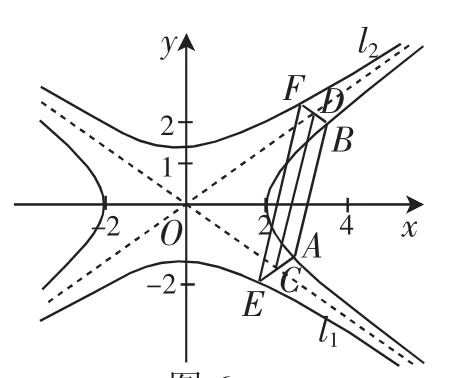
圖6

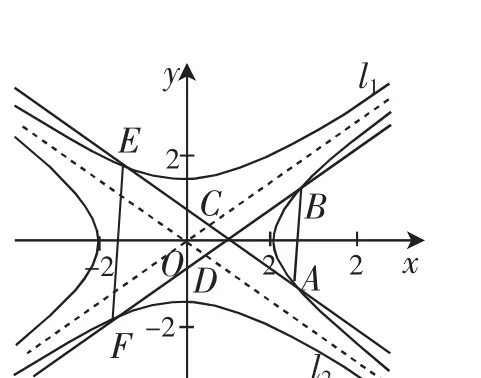
圖7

證明：通過線性變換（*）將雙曲線C1，C2變成等軸雙曲線C1′：x′y′=1和C2′：x′y′=-1，漸近線變成坐標軸，相應的點變成對應的點，如圖8.設x1）.對圖形6的情形，則C′（x1，0），

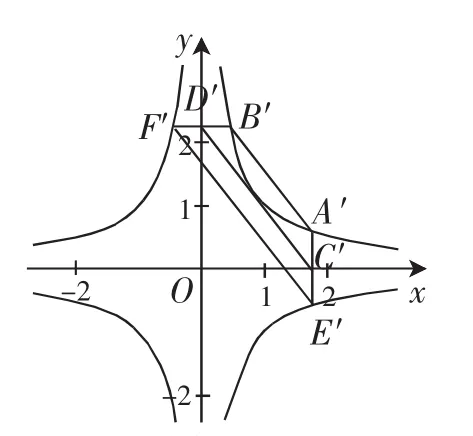
圖8

由線性變換性質2知，AB∥CD∥EF.

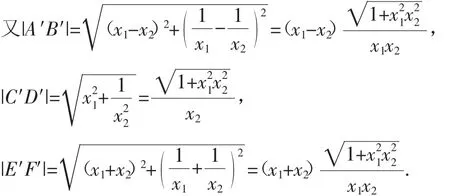
所以|A′B′|+|E′F′|=2|C′D′|，由線性變換性質5知，

2|CD|=|AB|+|EF|.

同理可證圖7的情形：2|CD|=|EF|-|AB|.

特別地，當A，B重合時，|EF|=2|CD|，即過雙曲線上任一點作兩漸近線的平行線被其共軛雙曲線截得的線段長是被兩漸近線截得線段長的2倍.

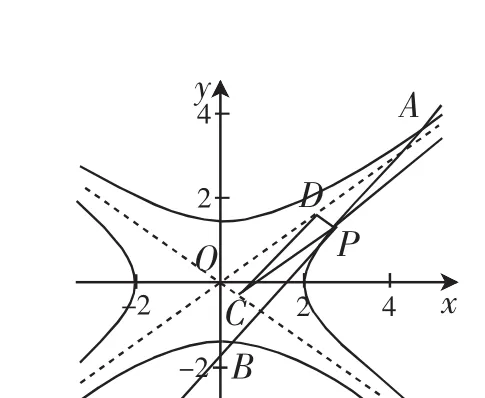
圖9

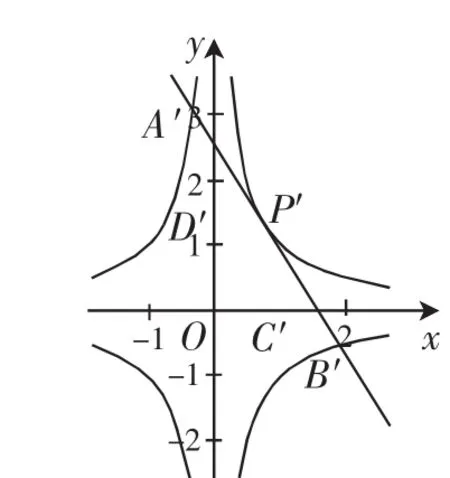
圖10

證明：通過線性變換（*）將雙曲線C1，C2變成等軸雙曲線C1′：x′y′=1和C2′：x′y′=-1，漸近線變成坐標軸，相應的點變成對應的點，如圖10.設

證明：通過線性變換（*）將雙曲線C1，C2變成等軸雙曲線C1′：x′y′=1和C2′：x′y′=-1，相應的點變成對應的點，如圖11.在C1上任取一點所以.由線性變換性質6知，

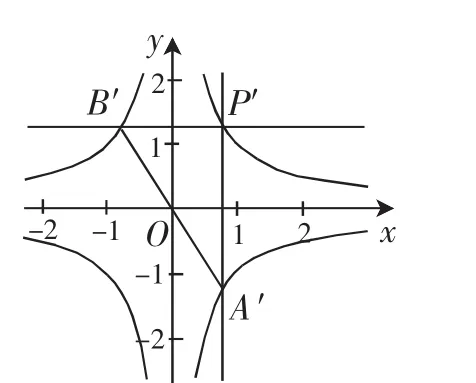
圖11

參考文獻：

1.趙忠華.雙曲線一個優美性質的發現［J］.中學數學（上），2016（2）.

2.陳良驥.雙曲線一個優美性質的簡證與推廣［J］.中學數學教學，2016（5）.

3.丘維聲.解析幾何［M］.北京大學出版社.

4.吳佐慧，林軍，劉合國.仿射變換在高中數學中的應用［J］.數學通訊.2015（9）.

5.呂佐良.雙曲線的一個定值性質及應用［J］.數學教學研究.1997（6）.J