數形結合思想在小學數學教學中的應用
高蘭

【摘要】本文論述有效運用數形結合的思想方法于小學數學教學中,可以促進數量關系直觀化,深化學生對數學知識的理解,提高學生解決問題的能力。
【關鍵詞】數形結合 小學數學 課堂教學
【中圖分類號】G 【文獻標識碼】A
【文章編號】0450-9889(2018)12A-0045-02
數形結合思想就是將數量關系與空間形式相結合,是經典的數學思想方法之一,通過數軸、線段圖、示意圖、模型或具體的生活情境中的實物、生活情形等形式將數量關系簡明化、直觀化,這種“數”與“形”的相互轉換、巧妙結合,使數學問題能化繁為簡、化難為易,從而得以解決。數形結合思想不僅可以幫助小學生深化對知識的理解,還可以為復雜的知識學習打下良好的基礎。
一、巧用數形結合,深化對數學知識的理解
數學是抽象的,但我們可以利用數形結合思想,將數學與生活結合,讓抽象的數學知識形象化。例如,在蘇教版數學五年級上冊《認識公頃》教學中,雖然筆者在課前帶領學生圍出100平方米,但要求學生僅僅在初步認識100平方米的基礎上學習1公頃還是存在困難的,因為學生很難想象出100個100平方米的大小。為了突破這一難點,讓學生深入體會1公頃的大小,筆者先讓學生圍出100平方米,初步感受100平方米的大小,在此基礎上利用課件依次出示100個100平方米的縮小圖,揭示100個100平方米就是1公頃。這樣震撼的畫面會引發學生的關注,讓學生初步感受1公頃的大。接著筆者借助生活中的實物圖例,通過課件向學生展示學校、操場及居住小區的三維地圖,在這些三維地圖中圈出1公頃,結合現實生活的情形進一步加深學生對1公頃的認識和理解,并鼓勵學生課后走一走這些地方,進一步感受1公頃的大。這樣教學,在有限的條件下簡潔明了地讓學生體會了1公頃的大小。這種將抽象的數據與生活中的實物圖形巧妙結合,借助圖形將數據直觀化,符合小學生以具體形象思維為主的認知特點,順利突破本節課教學的重難點。
二、運用數形結合,培養解決問題的能力
蘇聯教育家維果茨基提出:教學應著眼于學生的最近發展區,為學生提供帶有難度的內容,調動學生的積極性,發揮其潛能。因此,教師在教學時應充分利用數形結合思想調動學生的內驅力,促進學生積極思考,從而使解決問題的方法多樣化,激發學生的學習潛能。
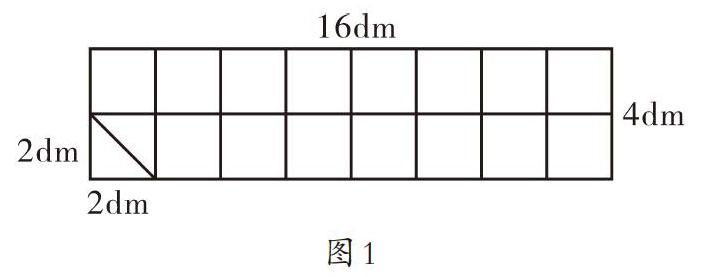
例如,用一塊長16分米、寬4分米的長方形紅布做直角三角形小旗,小旗的兩條直角邊都是2分米。這塊長方形布一共能做多少面小旗?
一般情況下,大部分學生都是用長方形紅布的面積除以三角形小旗的面積。但也有少部分學生通過畫出如圖1所示的圖形來解決問題。
三、妙用數形結合,理解數量關系
教師在小學階段的數學教學中,只依靠算式進行分析講解很難讓學生明白,這時教師要妙用“數形結合”,借助“形”來使數量關系直觀化。
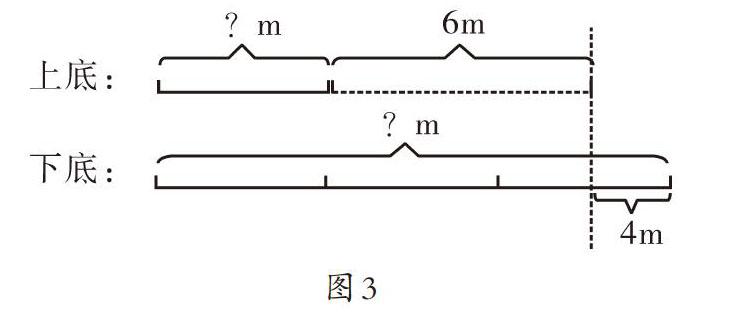
例如,一個梯形上底是下底的3倍,高是10米,如果下底減去4米,上底增加6米,它就變成長方形。梯形的面積是多少平方米?
從條件和問題出發,我們容易發現解答這道題的關鍵是求出梯形的上底和下底,學生找到關鍵點后,可能嘗試畫出以下圖形(如圖2):
利用線段圖來解決問題,角度新穎,且線段圖同樣也可以將數量關系直觀化,同時還體現了部分學生已經能夠自覺運用數形結合思想解決較為復雜的數學問題,對線段圖的運用較為靈活。學生不是從頭腦中已有的方法尋求答案,而是結合具體問題具體分析,將數形結合思想進行遷移。因此,教師在教學時要充分利用典型題增強學生的求新意識,激發學生勇于創新的精神。
綜上所述,要讓每一個學生都能有所發展,教師要教的不僅僅是數學知識與技能,還要讓學生銘記數學精神、靈活運用數學思想及方法,經歷數學活動的探究過程,積累數學活動經驗。教師要有計劃、有目的地滲透數學思想及方法,使學生逐步形成數形結合的思想,并能夠靈活運用數形結合思想方法解決數學問題,拓寬思維的深度和廣度,培養學生的創造性思維,提高學生學好數學的自信心。
(責編 林 劍)

