元素周期表的物理本質及其思想啟示

摘要： 早在20世紀20、30年代建立量子力學的過程中，從自由原子的外形必須是球狀的事實出發，單憑對稱性的分析即群論就已經把元素周期表的本質完全回答清楚了。具體說來，屬于Lie群的球對稱就把原子中單個電子的狀態約束在球諧函數或其線性組合之中。從那時候起，“化學不再是單純實驗科學”的時代悄悄來臨;“化學有化學的規律”那種排斥物理學的觀點開始失去影響力。既然可以預期未來不可能制備出非球狀且相對穩定的自由原子，因此就不可能指望元素周期表在未來有本質的改變。

關鍵詞： 元素周期表;群論;科學實驗;理性思維

文章編號： 10056629（2018）3000309 中圖分類號： G633.8 文獻標識碼： B

“用物理學的火炬照亮化學的暗室。”

——Friedrich Wilhelm Ostwald （1853—1932年。物理化學學科奠基人，1909年諾貝爾化學獎得主）[1]

“化學不再是門單純的實驗科學”

——1998年諾貝爾化學獎頒獎公告的補充資料[2]

1869年門捷列夫發表第一個元素周期表標志著第一個化學規律的建立。很長時間內，人們都知道那還僅僅是周期表的浮出，不是周期表的確立，很多人隨之繼續試圖揭示它的本質。今天的化學史學者告訴我們： 在發現元素周期表的過程中，曾經先后試過按原子量遞增猜測、按性質的三分組猜測、“八音律”猜測、門捷列夫的猜測，和按原子序數遞增的嘗試，逐步形成目前形式的元素周期表[3～6]。

當然，元素周期表是關于化學元素總體化學行為的描述，不包括細節問題的描述。至于細節問題，如形成陶瓷、晶體、熔點……行為規律的描述能力，那就要另外畫一張更深層次上的表，那顯然不屬于大多數化學家心目中的元素周期表。

很長時間以來，化學界關于元素周期表本質的認識： 要么是回顧歷史過程，可那是個猜測的歷史;要么遇到化學性質難以數值化的困難;即便想從電子結構考慮，可薛定諤方程宛如一層不透明的外殼，難以透過它發掘隱藏在化學性質背后的物理本質[7～10]。于是，有些中外化學家認為對元素周期表本質的認識還有待發現，他們把希望寄托在未來的科學發展，包括新元素的實驗發現、穩定島元素的實驗合成、相對論效應的探索……等等，加深對元素周期表的認識[11～14]。

可是，本文卻要向化學界傳達如下信息：

（1） 對元素周期表物理本質的認識是在量子論發展的過程中順帶完成的。早在1950年代之前就搞清了周期表的物理本質在于： 一是原子核電荷Z的因素;二是自由原子外形的球對稱決定了原子內電子狀態的角分布;這兩個物理根源： 核電荷與球對稱;在化學界，前者人人都知道，而后者知道的人卻不多。

（2） 元素周期表表達的是原子的化學行為，而化學行為的物理根源在于電子的行為（或電子的狀態）。核電荷是電子狀態的第一位決定因素，自由原子的球對稱是電子狀態的第二位決定因素。前者用Bohr舊量子論來理解就是決定了主量子數n;后者單憑Lie群就可以從球對稱求得電子云的角分布，即角量子數l=0， 1， 2， …， n和磁量子數m=-l， -l+1， …， l-1， l。

（3） 所以，元素周期表的物理本質已成定論，未來的科學不可能改變它。

本文不談元素周期表外表形式的多樣性或藝術性，只談周期表的物理本質，由此重新認識化學思想的基礎。

1 對元素周期表物理本質的認識

周期表既然是一張表，就要排序，排序要有數字。最早，J. Dalton選中原子量這個數字，也顧不上追究別的因素，先排好再說。此后，大多數學者包括門捷列夫都采用“性質”來排序。雖然門捷列夫掀起了化學界對周期表的一場普遍關注，但化學性質是個種類繁多、界定含糊且很難數值化的概念。性質相似是件很難辦的事。所以在不知道電子、不知道原子內部結構的整個19世紀漫長歲月里，周期表只能猜這猜那，徘徊不前。盡管真正的科學幾乎總是從猜測開始，猜測極為可貴，但只有緊緊追究物理根源才能走出猜的迷津。

1.1 一場史無前例的物理學革命

從1895年Roentgen發現X射線開始，一直到1913年Bohr提出原子模型之間，一系列重大發現掀起了一場史無前例的物理學革命。人們確定了原子、分子的存在，知道了X射線、電子、放射性、光電效應、早期量子論、原子光譜……，最后對構成物質的基本單元原子有了大致正確的認識。也正是在這場世紀之交的物理學革命中，出現了理論物理學這門學科。原先認為“物理學是一門實驗科學”，那時開始認識到“物理學不是一門單純的實驗科學”。不少數學家加入到理論物理學家行列中。同時也認識到雖然實驗是理論的基礎，但是單憑實驗數據的統計擬合卻不能逼近科學真理，“定量化”與正確的科學理論決不是一回事。

1.2 周期表走出猜測的關鍵第一步

在這場物理學革命中，荷蘭律師兼業余物理學家A.Van den Broek和英國物理學家H. Moseley的工作對周期表的形成起著決定性的影響[15， 16]。1909年英國物理學家C.G. Barkla（1877～1944）發現同一元素的不同材料發出的X射線中有幾條譜線是該元素的特征譜線，與其化學狀態無關。1911年Rutherford根據α粒子通過鋁箔、金箔的散射實驗發表了原子的有核模型。一個月之后，Van den Broek就憑著他對周期表的業余研究和Rutherford的實驗發表文章直接猜測原子核的核電荷Z就是該元素在周期表上的順序號。要知道，那時其他科學家就根本沒有把周期表上的順序號當作物理量，雖說Van den Broek也是猜測，但是他第一個直指其中的物理根源。

圖1 1911年著文猜想核電荷Z就是該元素在周期表上順序號的A. Van den Broek（1870～1926，左）和用X射線散射實驗來驗證Van den Broek猜測的H. Moseley（1887～1915，右）

為了驗證Van den Broek的猜測，Rutherford的助手Moseley對X射線與各種物質的相互作用作了系統研究，根據X射線中Barkla指出的特征譜線，發現其頻率的二次方根與該元素在當時按原子量排列的元素周期表中的順序號成線性關系（Moseley定律），但有少數元素不符合。Moseley認識到： 根據原子的Rutherford有核模型和Bohr的舊量子論，既然這些特征譜是X射線導致原子內層電子躍遷產生的，憑那時人們知道的經典電磁學，外層電子是不會對內層電子起靜電屏蔽作用的，不同元素的內層電子所受到外部作用的差別只能來自核電荷的差別。所以特征頻率只能與原子核所帶的正電荷數有關系，與外層電子無關。Moseley驗證了Van den Broek的猜測，找到了周期表的第一個物理根源。Moseley是第一個用物理學方法整理了周期表中元素的排序，認為核電荷才應該是影響化學性質不同的主要物理根源[17， 18]。把按核電荷排列的元素順序號稱為原子序數。

盡管Moseley定律還是唯象的，不甚嚴格，但是后人根據Moseley定律得出： Van den Broek的原子序數就是核電荷Z的結論是正確的，有明確的物理含義（那時Moseley根據Bohr的舊量子論以為原子序數是Z1[19]）。今天說的原子序數是Van den Broek的原子序數，不要把它混同于此前的元素順序號，兩者有本質的區別，前者有物理意義，而后者沒有。今天的原子序數首先是核電荷數Z的同義詞，其次才是元素的順序號。元素順序號僅僅是數字排序，沒有物理意義。按照Van den Broek的原子序數重新排列是周期表走出猜測迷津的關鍵第一步。

1.3 周期表走出猜測的關鍵第二步

世紀之交的物理學革命中，理論與實驗的互動，導致1925到1930年代間在舊量子論的基礎之上建立了量子力學，其中解釋原子、分子光譜是關鍵課題之一。德國數學家Hermann Weyl（1885～1955）、美籍匈牙利數學家John von Neumann（1903～1955）、美籍匈牙利理論物理學家Eugene Wigner（1902～1995）和荷蘭理論物理學家Hendrik Casimir（1909～2000）運用群論成功地對原子光譜作出量子力學的正確解釋[20， 21]。這件事更重要的意義在于，開啟了對稱性研究這樣一條揭示物理學根本規律的重要途徑[22]。這個過程中隨帶也把元素周期表余下的物理本質問題徹底搞清了。

圖2 Lie群的創立者挪威數學家S. Lie（1842～1899，左一）。德國數學家Hermann Weyl（1885～1955，左二）和美籍匈牙利理論物理學家Eugene Wigner（1902～1995）。1963年Wigner因群論運用于量子力學、原子光譜而榮獲諾貝爾物理學獎。

元素周期表走出猜測迷津的關鍵第二步，其本質在于對自由原子幾何上屬于球對稱的理性思維。因為是球對稱，所以要用到群論中的一支——Lie群。憑原子的球對稱就解決了周期表第二個物理本質問題。因為Lie群連物理學家都頗感難懂，所以知道此事的化學家不多。

2 群論是門什么學問

群論是一門數學。1832年5月底一位20歲、被法國巴黎高等師范學校開除的、激進革命派學生E. Galois，趕在他自知無望的決斗前夜急匆匆地將他的所有數學成果狂筆疾書下來，在三頁紙的最后寫下“我沒有時間了”。他死后11年，這篇文稿才被數學界肯定，認為盡管文稿表面上根據多項式方程的對稱性討論方程的可解性，但它標志著群論學科的誕生。

群論雖說是從研究對稱性引起的一門數學分支，但是很長時間內只有數學大師們才認識到群論在數學中的極高地位，認為群論是現代數學中概括性最強、影響最大的分支。S. Lie說：“群能解決一切問題。”F. Klein說：“群把整個數學統一起來了”。H. Poincaré說：“群論就是那拋棄其內容而化為純粹形式的整個數學。”I. Gelfand說：“全部數學就是某種類型的表示理論。”表示理論是群論中的一種理論，它將抽象的群元變換成可以具體操作的對象。表示理論將數學中貌視不同的各個分支貫通起來，所以說群把整個數學統一起來了[23， 24]。

零散的知識不是科學，知識被系統化繼而形成統一、自洽的理論之后才是科學。群論就是將數學各分支系統化、貫通成整個數學理論框架的學問。后來，群論這門數學分支，它在物理學中也達到極高的地位。不過，它外表高度抽象，早期還阻礙了物理學家對它的理解，甚至1930年代第一流的量子物理學家如P. Dirac、 J.C. Slater都曾反對群論用于物理學，誤以為太復雜，斥之為“群瘟”。現在群論已經成為現代物理學中最有用的數學理論之一。

群論運用于物理學、化學的基本思想在于： 對于自然界的許多規律，哪怕我們對其物理具體內容還不知道、實驗證據還不足，但是可以單憑問題中明顯可見的對稱性質，就可以從理論上演繹出一些重要結論，盡管這些結果不是體系性質的全部行為，但卻是體系必須嚴格服從的約束。對稱性的數學表達和演繹靠群論。群論大大推動了20世紀很多基本物理問題的預言和成功解決。例如，分子光譜的理解、大多數基本粒子的預言和發現都靠群論[25， 26]。

3 薄膜機械振動的啟示

為了通俗地介紹Lie群是怎么回答元素周期表的第二個物理本質的，為什么單憑原子的球對稱就可得出周期表余下的物理本質？我們先通過敲鼓時鼓皮振動的實例，來說明對稱性對體系的約束。

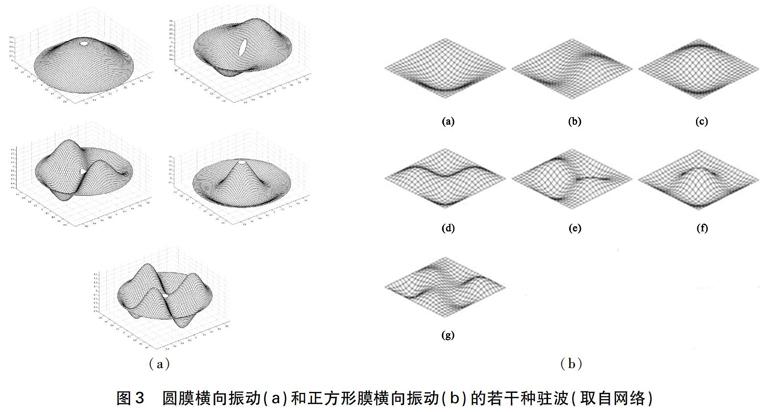
粗淺地看，可以把原子中的電子看成在一個球形外殼內處于“共振”的狀態。倘若不能形成“共振”的狀態，由于波的相位關系發生振幅的自身抵消，以致無法穩定存在。只有處于某幾種頻率和振幅分布的情況下，波的振幅非但不發生自身抵消，反倒自身增強，進而達到穩定的共振狀態。稱為“駐波”。這就是為何初等量子力學往往把原子中能夠穩定存在的電子狀態也看成是能夠形成駐波狀態的原因。樂器、音叉的發聲都屬于同樣的道理。一定幾何形狀的音叉有其固定的發聲頻率。不同外形造成不同的駐波狀態，對應的能量也不同，即駐波的振幅、頻率和能量與外殼的幾何形狀直接有關。

（a）

（b）

圖3 圓膜橫向振動（a）和正方形膜橫向振動（b）的若干種駐波（取自網絡）

敲擊鼓皮使鼓皮橫向振動就會發出聲音。圖3就是圓膜和正方形膜橫向振動的幾種駐波的振幅分布的數值模擬圖（前者相當于蒙在圓形鼓箍上的鼓皮，后者相當于蒙在正方形鼓箍上的鼓皮，盡管從來沒見過這個樣子的鼓）。無論圓膜和正方形膜的橫向振動問題服從經典力學的同一個二維波動方程：

2ut2=a22x2+2y2u

其中u（x， y; t）表示在任意時間t、膜上任意位置（x， y）處膜的橫向振幅。上式涉及微分稱為微分方程。要注意： 微分方程是局域的，即只代表某個時間、某個位置處那一小塊膜的振動行為，不代表整張膜的全局（即整體）的行為，所以若要根據微分方程求解全局行為，那還需要額外的條件，稱為邊界條件。不同的邊界條件有不同的解。在這點上與解代數方程不同（代數方程一般不需要額外條件）。膜振動的邊界條件就是在圓周或正方形邊框處的振幅必須為零（即因為鼓皮邊緣釘在鼓箍上，所以顯然鼓皮的邊緣是無法振動的）。圖3中圓膜和正方形膜的駐波形狀稍有不同，根源來自各自的邊界條件不同。

既然自由原子中電子的狀態是在三維球體內的駐波，而圓膜的振動波可看成是在二維“球體”內的駐波，它們服從的微分方程都屬于波動方程，只是維度的不同;所以可以設想兩者有對應關系。

圖3（a）畫出圓膜橫向振動的無窮多種駐波方式中的五種。其中自上到下、從左到右分別與原子中電子軌道中的1s、 2px、 3d、 2s和4f在某個截面上的波函數很接近。圖3（b）畫出正方形膜橫向振動的無窮多種駐波方式中的七種。其中自上到下、從左到右分別與原子中電子軌道中的s、 px、 py、 dxy、 dx2-y2、 2s和4fx（x2-3y2）在某個截面上的波函數很接近。這里只是接近而不是完全相同，原因有兩個： 一則兩者屬于不同維度的問題（膜振動是二維駐波，而電子波函數是三維駐波）;二則兩者的邊界條件不同，前者的振幅在圓膜邊緣為零，而原子軌道的邊界條件是在無窮遠處才為零。

需要注意圖3畫出的是某個瞬間的振幅，振幅可正可負;若此時某處振幅呈正值，在半個周期后的時刻該處的振幅就處于負值。振幅的平方正比于能量密度（該處單位面積膜具有的振動能量）。圓可以看作二維空間中的球，于是，讀者可以不必顧忌振幅的正負值而看出圖3（a）符合二維情況下的球對稱性： 一個s的平方是“球”對稱的（二維“球”）;一個px的平方加上一個py的平方也是“球”對稱的;一個2s的平方也是“球”對稱的……。

還可以設想，若邊界條件從二維圓形過渡到二維正方形，或過渡到三維球形，盡管在任意點的鄰域范圍內，即局域意義上，服從同一個微分方程（本例是波動方程），還是可以設想三種邊界條件的駐波振幅之間是能夠過渡的。

與膜振動的例子類似，二胡演奏家手指在弦上滑動造成音調變化，也是微分方程改變其邊界條件造成解的全局變化的一個實例。

微分方程在物理學、化學中具有舉足輕重的意義。離開微分方程就無法建立現代科學（所以牛頓要發明微分來建立他的力學）。擴散方程、導熱方程、波動方程（即振動方程）都是微分方程。要準確回答化學反應中的行為也離不開求解微分方程。微分方程描述體系在任意時刻、任意空間位置處的局域行為;不是體系的在整個時間、空間位置范圍內的全局行為。全局行為應當是個函數或泛函（當自變量本身就是函數時的一類標量值函數稱為泛函，電子的能量就是波函數的泛函）。顯然，只靠微分方程是無法求得體系的全局行為的。為了根據微分方程求得整個體系的全局行為還必須知道體系的某些（但不是全部）有關全局的信息。

邊界條件（或初始條件）只是全局信息中的一種，體系更為重要的一種全局信息是體系全局的對稱性。體系的對稱性有的是外觀上的，有的是內在的，也可以是時間上的。總之，根據微分方程再加上若干體系全局的信息（即條件）就可以徹底求解體系的全局行為。

鼓膜振動問題和原子中的電子結構問題的微分方程雖說都屬于波動方程，但畢竟一個是宏觀問題，另一個是微觀問題，一個要解經典的機械振動的波動方程，另一個要解薛定諤方程，還是有點差別的。同時，從上述圖3（a）圓膜振動與氫原子的波函數兩者的對應關系看到： 我們實際上關心的不是整個解，而是關心其角分布。思索一番，又看到恰恰這部分在物理上就是由體系的球對稱性造成的。

所以就聯想到： 能否不去具體解微分方程，只是單憑它們共同的對稱性來窺視體系全局行為中我們最關心的那一部分呢？答案是可以的。不解微分方程，單憑它們共同的球對稱性就可以將其全局行為中的共同部分嚴格地演繹出來。演繹的方法就是Lie群。

4 單憑Lie群就可以得到元素周期表的第二個物理本質

因為同一種化學元素，其行為與其存在的狀態抑或是固體、液體、氣體還是哪種化合物都有關，都會有不同的行為;所以元素周期表討論的元素實際上一定是該元素處于自由原子狀態的。不然，這個周期表就太大了，無法方便使用。

4.1 自由原子的球對稱性

什么是自由原子呢？為什么說自由原子的外形一定是球形，或其核外電子云一定呈球對稱的呢？進而又是怎么用Lie群來演繹得到其中的物理本質呢？

自由原子就是不受外界作用的、孤零零的一個游離原子（無論是否發生過電離）。拿類氫原子為例，核電荷Z+位于球心，核外一個電子呈球狀分布。即使對于任何元素的原子，

根據庫侖定律之平方反比律就

可以理解： 只要其他原子距離很遠，以致對我們討論的那個原子的作用小到可以忽略，那么討論的對象就是一個自由原子（或自由離子）。所有的自由原子其原子核位于球心，核外電子一定呈球狀對稱的分布。

萬一自由原子的電子云不圓，即偏離球對稱，某處的電子云突出球面，而另一處電子云從球面癟進去一點。那么，那樣的電子云一定不能保持穩定狀態。可以證明： 只有電子云從突出球面的那部位填補到癟進去的部位，正好讓整體成為球對稱，才能使整個原子重新恢復電子的穩定狀態。

對稱性是體系的一種全局性質。化學家熟悉的對稱性有晶體外形的對稱性、分子結構的對稱性和原子、分子軌道的對稱性。不用先求分子軌道的具體解，人們就可以單憑分子結構的對稱性，從群論得出可能存在的幾種分子軌道及其能級分布。不符合對稱性的軌道一定是不存在的。不過，化學家熟悉的以上對稱性都屬于離散群，即對稱群中的對稱操作（即群元）總數為某個有限大的整數。

但是，對于自由原子那樣屬于球對稱的物體，在指定通過球心的旋轉軸后，繞軸旋轉的角度是可以連續變化的、總數無窮大的實數值[0， 2π），所以旋轉群屬于連續群，群元總數無窮大，需要用群論中的Lie群方法[27， 28， 29]。

4.2 Lie群方法解球對稱性問題

Lie群的基本概念是只需考慮恒等變換附近的無窮小變換。就可以把研究無窮多個群元的Lie群的表示問題化為研究有限個無窮小生成元的表示問題，即Lie代數的表示問題。找到了Lie代數的不可約表示也就找到了Lie群的不可約表示。在物理學中常常遇到這樣的情況，Lie代數很自然就看出來，而對應的Lie群卻不一定有簡單的物理解釋。

從圖3可以定性看出，同時也可以用群論嚴格證明，符合某種對稱性本質上就是描述該體系整體行為的任意函數一定要受到該對稱性的嚴格約束，不符合對稱性的函數一定不是問題的解。Lie群理論[30]證明了三維旋轉球對稱所屬的SO（3）群或SU（2）群的第Ⅱ類可對易的完備算符集，其共同的本征函數集就是球諧函數：

Ylm（θ， φ）=（-1）（m+|m|）/2（2l+1）2（l-|m|）！（l+|m|）！

P|m|l（cosθ）12πeimφ

其中P|m|l（cosθ）為聯屬Legendre多項式，l=0， 1， 2， …，和m=-l， -l+1， …， l-1， l。

換言之，這一組球諧函數{Ylm（θ， φ）}在方位角θ=[0， π]和φ=[0， 2π]區間內構成一組正交歸一完備函數集。什么叫完備函數集呢？那是指只要是球對稱的體系（不管是宏觀或微觀），描述該體系所有可能狀態的函數必定且可以展開成上式這一組函數的線性組合，這一組函數就稱為是完備的函數集。“完備”意味著這樣的表述是嚴格的、天衣無縫的，且不可能由其他函數集來展開。例如，不同頻率的正弦波全體可以描述任意平面波，卻不能用來描述具有球對稱體系的球面波狀態，哪怕只描述其中一個球面波也做不到。l=0， 1， 2， 3， 4， 5， …分別就是s， p， d， f， g， h， …狀態;每個l具有2l+1個不同的m狀態。狀態有可能是宏觀狀態也可能是微觀狀態，取決于具體是宏觀還是微觀體系。以上Lie群求解的過程只限于討論三維空間的球對稱體系，并未限制體系是哪個具體體系。

所以對于自由原子，不用求薛定諤方程，單憑Lie群就可以得到其中電子軌道的部分信息。因為這里討論的三維空間只有（θ， φ）兩個方位角，可見Lie群給出的解其實是電子狀態的角分布。結果表明： 自由原子中的電子狀態的角分布與解薛定諤方程得到的類氫原子中的電子狀態的角分布是完全相同的，可謂殊途同歸。

總之，單憑Lie群就可以得到元素周期表除了原子序數之外的全部內容。無論在未來發現新元素的實驗、穩定島元素的合成實驗、相對論效應的探索……等等實例中，都可根據平方反比律預期它們穩定的自由原子也必定是球對稱的，球對稱的約束必然進而造成對其中電子狀態角分布的約束一定呈球諧函數。除了把電子填入s， p， d， f態（分別在周期表中占2、 6、 10個位置）外，還有g態[（2l+1）l=4×2=18個位置，乘以2來源于自旋]，甚至h態[（2l+1）l=5×2=22個位置]……。球對稱性是限定周期表的第二個物理根源，儼如如來佛的手掌怎么跳是跳不出去的。這是周期表走出猜測的關鍵第二步。

當然上述超重元素、穩定島元素的穩定自由原子，只是指電子狀態，而不是原子核的狀態。合成這兩類元素實際遇到的最大問題是原子核的狀態極不穩定，即半衰期極短，以至于來不及完成各項快速測量實驗，就已經變成別的元素了。原子核的穩定性不屬于元素周期表的討論范圍內。只要原子核衰變足夠慢，由于電子質量比原子核輕得多、運動也就快得多，自由原子就一定是球狀的，也就一定能夠在現有的周期表框架內找到合適的位置。因為那個位置就代表了該元素的電子結構，繼而利用周期表估計它的化學性質。所以，未來出現的超重元素、穩定島元素……不可能改變元素周期表的格局。同理，相對論效應也不可能改變周期表的格局。

4.3 在群論面前的《周易》

有些學者聲稱可以運用《周易》的陰陽八卦理論探討元素周期表問題[31]。其實，只要看任意一本群論入門書的前10頁，反復幾遍、思索一番，很容易看出： 即便用現代數學的概念把《周易》陰陽論的含義抬高，充其量也只是個二階群C2;所謂黑白、陰陽、男女……之間的“由此及彼”的關系就是C2群中的兩種群元： 恒等元I和C2元。C2群是最簡單的一種群，只代表最簡單的的一種事物間的關系（即對稱性）。而自然界萬物間存在的關系實際上遠不止二階群一種，還有好多種群，代表更復雜的事物間的關系。

群之間可能存在從屬關系，一個群可以是另一個群（有嚴格數學表達）的“兒子”關系，稱為子群。例如二階群是三維旋轉群R3的子群。R3又是代表球對稱的SO（3）群或SU（2）群的子群。上述自由原子的球對稱性就屬于SO（3）群，不屬于二階群，或二階群只是SO（3）群的一個子群。既然子群的完備集不可能也是“母”群的完備集，所以二階群的《周易》是絕對無法理解元素周期表球對稱的本質的[32]。

不要遇到s， p電子有2+6=8，就非要與《周易》八卦中的“八”硬湊在一起。即使湊上幾個元素，此后d， f電子的10與14怎么湊呀？將來g， h電子的18與22又怎么湊呀？憑群論就可以斷言這樣的硬湊毫無價值。

兩千年之后，人們還陶醉在《周易》陰陽論這二階群中，誤以為萬物之間只有這一種事物間的關系。他們沒看到自然界中萬物之間還有很多種其他關系（很多種群），那是明擺的現實。宇稱也屬于一種群，難怪，以破除宇稱守恒定律著名的楊振寧先生一眼就看出問題，振聾發聵地指出： 《易經》影響了中華文化中的思維方式，是近代科學沒有在中國萌芽的重要原因之一[33]。

5 揭示元素周期表本質帶來的啟示

上述單憑自由原子的球對稱通過李群就完整地揭示了元素周期表的第二個物理本質和根源，至少在1950年代就已經清楚了。從它對周期表本質的揭示，我們可以看到如下三個啟示。

5.1 啟示一：化學不再是門單純的實驗科學

福井謙一先生（1981年諾貝爾化學獎得主;1918～1998）說他當學生的1940年代，“化學被看作一門如果不進行實驗就什么也不清楚的學科”[34]。的確，在1998年之前，可以說化學界的主流思想（少數物理化學家除外）幾乎清一色地主張“化學是一門實驗科學”，“化學有化學的規律”。在中國，長期以來尤其是80年代以前，起碼在國內化學界的主流思想是： 化學是實驗科學，化學有化學的規律。只有到1998年年末諾貝爾化學獎頒發給兩位理論化學家J. Pople和W. Kuhn時，頒獎公告的補充資料中說“化學不再是門單純的實驗科學”[35]。

其實，化學早就不是門單純的實驗科學了。就拿確定原子、分子是否存在的問題為例： 很多人以為是1908年法國人J. Perrin在顯微鏡底下觀察懸浮液中藤黃粒子的布朗運動解決的。但這不是故事的全部，事實是，此前1905年Einstein在分子假設下根據隨機行走模型就演繹出懸浮液水平方向布朗粒子的運動規律〈x2〉=2Dt。另一個是Boltzmann根據統計力學提出的懸浮液垂直方向的沉降平衡公式。

有了這兩個理論公式，Perrin才知道朝哪個方向去做實驗。最后1908年Perrin實驗驗證成功，確立了原子、分子存在的觀點。Perrin的高明之處在于，他意識到： 絕大多數對宏觀物體的實驗測量實際上測量到的是物體中無窮多個組成粒子微觀行為的平均行為，即集體行為，而不是個體行為，換言之，在一般的實驗中通常都是“抹平”而非“突出”微觀粒子的個體行為;恰恰是Einstein公式提供了“間接”窺視微觀粒子個體行為的機會。所謂“間接”指的是： 人們直接看到的是一個藤黃粒子的運動，從而斷定推動該藤黃粒子只能是在它周邊的水分子，其總數要遠遠少于整個體系中水分子的總數，這就造成實驗窺視個體行為的機會。

在化學史（尤其是物理化學這門分支）中，還有其他相當重要的實例，如化學鍵的本質與自旋配對、固體比熱、共振論等，都說明了化學早就不是門單純的實驗科學了。1870年代出現的物理化學學科是化學界中最早重視物理學、數學的分支。當時其奠基人F.W. Ostwald主張“用物理學的火炬照亮化學的暗室”[36]，即化學的道理都要到物理學中去找。在1900～1930年代的那場物理學革命中，物理化學家M. Curie、 A.A. Noyes、 L. Pauling、 R.C. Tolman、 R.S. Mulliken和G.N. Lewis等也積極參與其中。發展出放射化學、結構化學和量子化學等化學學科。對化學界影響最大的莫過于Pauling的書《化學鍵的本質》。Pauling的共振論使得整個化學界都開始驚動了。引起了保守者們的不滿，代表人物是當時著名的化學權威英國有機化學家H. Armstrong[37]，他說：“事實是，物理化學家從來不運用自己的眼睛，最可悲的是缺乏化學教養。我們應該把這些物理因素徹底地從我們中間剔除出去，并回到我們的實驗室里來。[38]”

其實既然知識被系統化、繼而形成理論之后才是科學;同時物理學和化學都關心同一個物質世界，那么就沒有任何理由強調“化學有化學的規律”。Armstrong畫地為牢，抵制物理思想，顯然是錯誤的。可是不知什么原因，這種強調“化學有化學的規律”的思想在90年代末之前我國的化學界中還是居于主流地位的。原因之一可能是化學史家往往關心古代史、關心各類化學品產品的開發史，而對化學思想起到根本影響的物理化學學科的思想史關心不夠。

5.2 啟示二： 經驗不能替代理性思維，數學的理性思維也是檢驗真理的判據

化學家都感到化學知識缺少定量表述。于是，長期以來很多化學家以為： 單憑實驗數據統計擬合就可以發現科學真理;實際上這是很大的誤解，屢次誤導化學家走上歧路[39]。任憑定量程度再高只能說明在統計數學意義上的精確程度，與物理意義上的正確決不是一回事;不是統計數學錯了，而是我們對統計數學的理解錯了，沒有看到“統計數學本質上是一種歸納推理”（統計數學大師R.A. Fisher語，1956年）。經驗不能替代理性思維。什么是理性思維呢？那就是運用數學的物理思維。

盡管數學有時也從經驗獲取靈感，可是一旦建立了數學的公理體系，在這個基礎上可以獨立發展起整幢數學大廈。數學抽象讓我們有能力對更大范圍的自然問題有一個統一、深入的物理認識，超過以往的經驗，獲取更高水平上的正確認識。

上述Lie群發現原子中電子狀態角分布的實例，上述1908年Perrin的布朗運動實驗驗證原子、分子存在的實例，都說明：“實踐是檢驗真理的唯一標準”中的“實踐”難道不包括數學的理性思維嗎？顯然應該包括在內。數學的理性思維也是檢驗真理的判據。

從牛頓萬有引力的F=GMm/r2，到庫侖定律中靜電力F=kq1q2/r2（那屬于化學家應該特別關心的問題），其中距離r的指數都是整數2而不是實數2，就體現了數學的理性思維。當時1772年的實驗結果是2.00±0.02，即指數的實驗精度為±2×10-2[40]。即便到了1971年指數的實驗精度高達驚人的±2.7×10-16，那還是沒有理由憑此確定該指數一定等于整數2，而不是實數2[41]。相比之下，今天的量子場論卻告訴人們： 庫侖定律中平方反比律的指數一定是整數2，決不是實數2;不然的話要出天大的問題： 會導致光子的靜止質量不為零，繼而出現真空中光速可變，黑體輻射公式要修改，電荷不守恒……，以致動搖了電磁學、相對論乃至整個物理學，今天我們賴以進入智能時代的科學基礎居然不見了？！顯然，有心力場的平方反比律不是實驗的結果，而是理性思維的結果，恰恰是它在關鍵點上超越了實驗，給我們對自然界的整個認識起了翻天覆地的變化。

另一個重要實例是計算數學家馮康（1920～1993）的故事： 馮康先生在“哈密頓體系的辛幾何算法”的工作是具有國際聲譽的成就，榮獲1997年國家自然科學一等獎;可惜這是個遲到的獎，是中國歷史上唯一一個給已故的科學家追授的一等獎。馮康的學術思想領先得太遠，以至于在他生前不得不經過一段冷遇、孤獨的歷程。創新程度越頂尖的科學成就和科學思想，越容易受到冷遇幾乎是個歷史規律。值得注意的是： 馮康先生用來給他的算法理論作驗證的七、八個關鍵例證，都是靠在數學上有嚴格解析解的數學模型，而不是其他[42， 43]。這又說明了： 數學的理性思維也是檢驗理論正確與否的判據，有時比實驗數據更有力得多。“理論受實驗的檢驗”不是像通常想象的那樣簡單。

或許有人問馮康與化學有什么關系？豈但有，非但直接有關，而且事關重大。正是因為國際上的化學界、生命科學界沒有及時認識馮康的思想，蛋白質結構的模擬計算一味盲目追求最大最快的計算機，至少貽誤了15年的時機[44]。

6 結束語

兩千年來，古今中外無不把哲學視為人類最高智慧的集大成者。但是自從16世紀以來，現代科學逐漸從哲學中分化出來，漸漸獨立成長。在回顧哲學與科學的關系中，正因為科學始終以認識大自然為己任，所以科學（包括化學）的思想發展也必定是最有活力的、最革命性的。

今天已經到了這樣的時代，連羅馬教廷都公開宣布對科學應取“謙卑的、刻苦的學習”態度。1979年11月教皇約翰·保羅二世（Pope John Paul II， 1920～2005），在向復查羅馬天主教會對伽利略平反的委員會的報告中說：“教會作為其保證人和見證人的神的啟示并沒有自行包括任何特定的科學理論，圣靈的幫助決不會有助于保證我們希望信奉的關于實在的物理構成的解釋。只有通過謙卑的、刻苦的學習，教會才能學會把他們的信仰的實質與給定時代的科學體系分離開來。尤其是當一種在文化上有影響的圣經讀本似乎與有義務承認的宇宙起源學說有聯系的時候。[45]”

盡管科學不是對人類社會與世界的全部認識，但是從科學活動獲得的正確思想不該受到漠視;恰恰相反，既然唯物主義者承認大自然存在的客觀性，就必須承認從客觀世界提取到的正確思想的獨立性和不可替代性。群論思想及其對自然科學（包括元素周期表）的認識就是其中的一部分。

致謝： 感謝北京大學化學與分子工程學院王祥云教授，與他的討論極具幫助與啟發。

參考文獻：

[1][36][38]T.哈格.鮑林——20世紀的科學怪杰[M].上海： 復旦大學出版社，1999： 67;148.

[2][35]The Royal Swedish Academy of Sciences. Press Release and Additional background material on the Nobel Prize in Chemistry 1998. http： //nobelprize.org/nobel_prizes/chemistry/laureates/1998/press.html陳敏伯.化學不再是純實驗科學[J].科學，1999，50（1）： 58.

[3][7][11]Scerri， E.. Selected Papers on the Periodic Table [M]. London： Imperial College Press， 2009.

[4][8][12]Scerri， E.. The Dual Sense of the Term “Element，” Attempts to Derive the Madelung Rule， and the Optimal Form of the Periodic Table， If Any [J]. Int J Quantum Chem，2009，（109）： 959～971.

[5][9][13]周佳偉，占小紅.尋求元素位、構、性的統一： 元素周期表的形成與發展[J].科學，2017，69（1）： 45～49.

[6][10][14][15]楊奇，高勝利等.再論化學元素周期表的形成和發展[J].大學化學，2017，32（6）： 46～67.

[16][31]徐道一.周易科學觀[M].北京： 地震出版社，1992： 159～168.

[17]關洪.原子論的歷史和現狀： 對物質微觀構造認識的發展[M].北京： 北京大學出版社，2006： 132.

[18][19]https： //en.wikipedia.org/wiki/Antonius_van_den_Broek.

[20]范·德·瓦爾登著.趙展岳，吳兆顏，王錫紱譯.群論與量子力學[M].上海： 上海科學技術出版社，1980.

[21]https： //en.wikipedia.org/wiki/Fasori_Gimnzium Gronau， H.D. eds.， 50th IMO – 50 Years of International Mathematical Olympiads， Springer， 2011.

[22]W.顧萊納.量子力學： 對稱性[M].北京： 北京大學出版社，2002： 1～8.

[23]劉培杰等編譯.Lie群和Lie代數[M].哈爾濱： 哈爾濱工業大學出版社，2016.

[24]況蕙孫，白銘復.物理學中的群論方法（上冊）[M].長沙： 國防科技大學出版社，1985.

[25]朱洪元.群論和量子力學中的對稱性[M].北京： 北京大學出版社，2009.

[26][27][30]陳金全.群表示論的新途徑[M].上海： 上海科學技術出版社，1984： 1～2，67～69，221～230.

[28]Thyssen， P.; Ceulemans， A.. Shattered Symmetry： Group Theory from the Eightfold Way to the Periodic Table [M]. Oxford University Press， 2017.

[29]Schwichtenberg， J.， Physics from Symmetry [M]. Springer， 2015.

[32]陳敏伯.評《周易科學觀》對元素周期表的解釋[J].科學文化評論，2005，2（2）： 108～117.

[33]http： //blog.sciencenet.cn/blog-39840-728842.html楊振寧先生2004年9月3日在人民大會堂舉行的“2004文化高峰論壇”上所做題為“《易經》對中華文化的影響”的報告.

[34]福井謙一.圖解量子化學[M].北京：化學工業出版社，1981.

[37]https： //en.wikipedia.org/wiki/Solvay_Conference.

[39]陳敏伯.單憑統計擬合能逼近真理嗎？論“憑什么相信計算”之三[J].化學通報，2016，（79）： 196～204.

[40][41]趙凱華，陳熙謀.電磁學[M].北京：高等教育出版社，2003： 50～51.

[42]http： //www.edu.cn/20041019/3118263.shtml馮端：“馮康的科學生涯——我的回憶”.

馮康，秦孟兆.哈密頓系統的辛幾何算法[M].杭州： 浙江科學技術出版社，2003： 1～11.

[43][44]陳敏伯.計算化學： 從分子模擬到理論化學[M].北京：科學出版社，2012： 112～119.

[45]Brown， R.H.， The Wisdom of Science： Its Relevance to Culture and Religion， Cambridge University Press， 1986.

李醒民譯.科學的智慧——它與文化和宗教的關聯[M].沈陽：遼寧教育出版社，1998： 162.