默會知識的激活與數學核心素養的培養

張勝黎

浙江省杭州市艮山中學 (310003)

20世紀有影響的科學家和哲學家邁克爾·波蘭尼在1958年發表的全面體現其哲學思想的著作《個人知識》中，對傳統的主客觀分離的知識觀進行了無情的批判. 他認為知識是客觀性與個人性的結合，具有默會的成分，在一定程度上是不可言傳的，由此產生了“默會知識論”.相較于能言傳的，可以用文字等來表述的明確知識，默會知識是指不能表述的那部分知識，且有著不同于明確知識的顯著特征：

(1)默會知識是鑲嵌于實踐活動之中的，是情境性和個體化的，常常是不可言傳的；

(2)默會知識是不能以正規形式加以傳遞的；

(3)默會知識是不能被加以批判性反思的.

雖然默會知識有著不同于明確知識的顯著特征，但并不表示兩者是對立的，兩者的關系可以用下圖的冰山模型來表示：

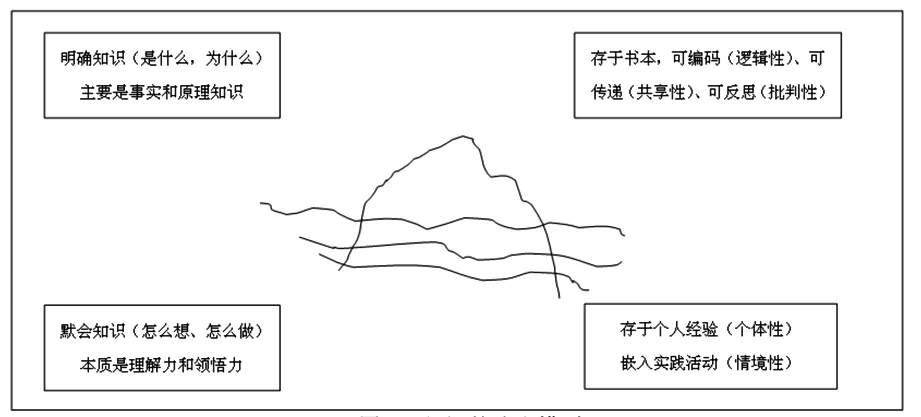
“知識的冰山模型”反映在數學上，說明了數學事實和原理知識的學習只是數學學習的冰山一角，還包含數學活動過程中數學能力的發展，也即默會知識的“激活”，而這種數學活動過程主要體現在用數學的眼光觀察問題、用數學知識與方法構建模型、通過由此及彼的聯想感悟事物的本質，這是應用數學解決實際問題的基本手段，也是推動數學發展的動力.

1．學會觀察，激活默會知識

任何聯系實際的科學研究都開始于觀察，抽象的數學也不例外，數學中的許多公理來源于對實際的觀察.通過觀察，使隱性知識轉化為顯性知識，從而激活默會知識.

例1 比較下列各數的大小：

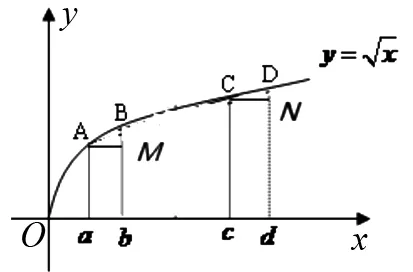
圖1

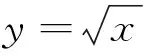
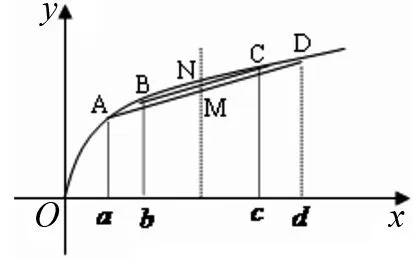
圖2

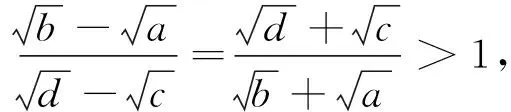
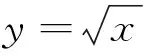
本題通過觀察函數圖像的變化特征，對一些表面上似乎不同的事物，能迅速地找出它們之間的相互聯系，透過表象抓住本質，這直覺判斷的背后體現了科學的洞察力.直觀想象也是數學的核心素養，它借助幾何直觀去感知事物的形態與變化，并利用圖形理解和解決數學問題.

2．實踐體驗，激活默會知識

數學家G·波利亞指出：“數學有兩個側面，一方面它是歐幾里得式嚴謹的科學，從這方面看數學像是一門系統的演繹科學；但另一方面，創造過程中的數學看起來卻像一門實驗性歸納科學.”數學實驗使學生在創設的問題情境中探索，在操作、觀察、討論、交流、歸納、猜想、分析和整理的過程中，理解數學問題的提出、數學概念的形成、數學結論的獲得與驗證以及數學知識的應用，讓學生養成參與實踐、自主探索、合作交流等積極主動的學習習慣.通過數學實驗，使原來較隱蔽的關系浮出水面，從而激活默會知識.

例2 下列兩個判斷是否正確：

(1)如果一個二面角所在的兩個半平面分別與另一個二面角所在的兩個半平面垂直，那么這兩個二面角的大小相等或互補.

(2)若∠BPC與平面α交于B,C兩點，點P在平面α外，點P在平面α內的射影為A，則∠BPC<∠BAC(即空間角小于射影角).

模型1：對于(1)，很多學生受平面幾何中“一個角的兩邊分別垂直于另一個角的兩邊，這兩個角的大小相等或互補”的啟發，用紙張做出了如圖3、圖4兩個模型，其中γ⊥α,δ⊥β，得出了“命題正確”的判斷.

模型2：部分學生考慮到從平面到空間不能作簡單的類比，而是以批判的眼光，作更深層次的思考.學生類比教室的門口,做出了如圖5的模型，當門轉動時，γ與δ組成的二面角的大小是變化的，但它始終能保證γ⊥α,δ⊥β的關系成立，從而得出了“命題錯誤”的判斷.

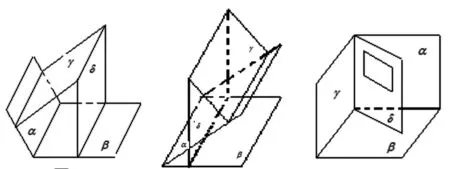
圖3 圖4 圖5

模型3：對于(2)，多數學生做出了如圖6的模型，并得出了“命題正確”的判斷.

進一步分析發現，如圖7，在ΔPBC中，使PA⊥BC，BA>CA，當PC以PA為旋轉軸轉動，在點C運動到點C′的過程中，∠CAB由180°逐漸變化到0°，∠CPB也逐漸變化到∠C′PB，容易觀察到∠CAB與∠CPB的大小經歷了由大于、等于到小于的漸變過程，從而得到了∠CAB與∠CPB的大小關系不確定的正確判斷.

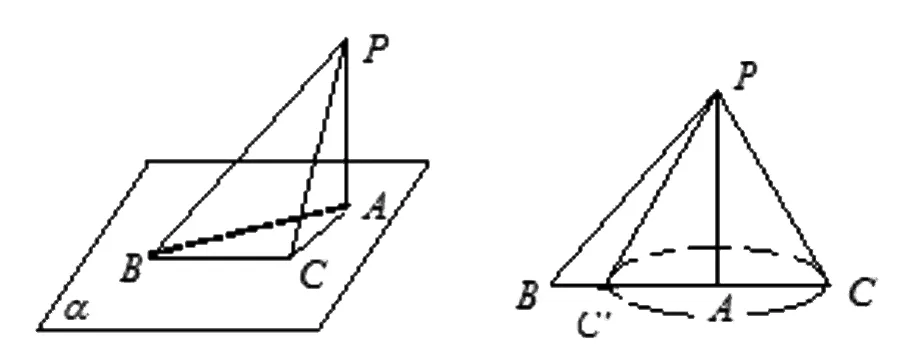
圖6 圖7

本例通過操作實驗，以批判的眼光，作出了正確的判斷.對于圖5和圖7的模型，只要我們把問題的真相揭示出來了，學生就能作出正確的判斷.這就是說，兩個模型在真相沒有揭示之前，相對于學生來說是默會知識，通過操作確認，把默會知識激活了，就轉化為了明確知識.

作為數學教學的重要方式，數學實驗與物理、化學實驗相比，不僅需要動手，更需要動腦，學生通過數學實驗操作去得到一些猜想或假設，經歷了數學結論的發現過程.在數學抽象核心素養的形成過程中，積累從具體到抽象的活動經驗，學生能更好地理解數學概念、命題、方法和體系，能通過抽象、概括去認識、理解、把握事物的數學本質，并逐漸養成一般性思考問題的習慣.

3．聯想發散，激活默會知識

想象以客觀的資料為依據，但又不拘泥于實際而有極高的抽象性，它是直覺的深化與外延的拓展，人們憑著想象來猜測研究對象的性質及其變化.客觀實際好比空氣，想象力好比翅膀，只有兩方面緊密結合，才能飛得高、飛得快、飛得遠.在分析觀察時，由于某事物的啟發，聯想到其他事物，導致新的發現，是激活默會知識的有效途徑.

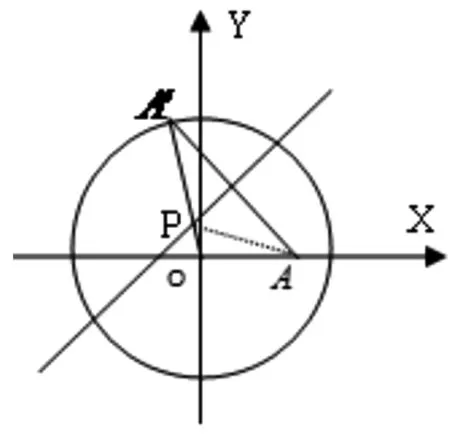
圖8

例3 (2003年全國高中數學聯賽一試15題)一張紙上畫有半徑為R的圓O和圓內一定點A，且OA=a.折疊紙片，使圓周上某一點A′剛好與A點重合.這樣的每一種折法，都留下一條折痕.當A′取遍圓周上所有點時，求所有折痕所在直線上點的集合.

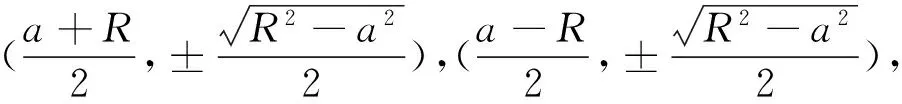
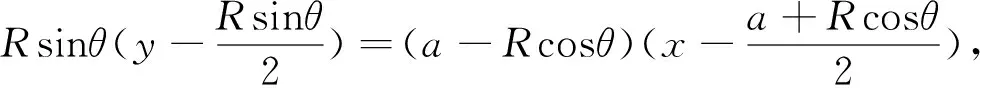
這個結果顯然是正確的，但這個結果肯定有違命題者的初衷，因為它沒有說明軌跡的形狀及區域范圍.那么怎樣來得到軌跡的顯性表示呢？

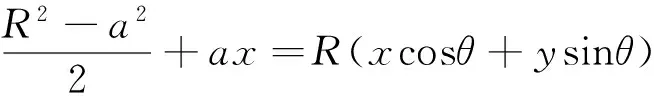
揭示本質：在高考模擬訓練中，常研究折痕與OA′交點P的軌跡，由對稱性可知，PO+PA=OA′=R，即點P的軌跡是以O、A為焦點，R為長軸長的橢圓.設M為折痕上任一點，則MO+MA≥OA′=R，即點M的軌跡是上述橢圓的外部及邊界.容易證明OP,AP與折痕的夾角相等，由橢圓的光學性質知，折痕所在直線與橢圓的邊界相切.

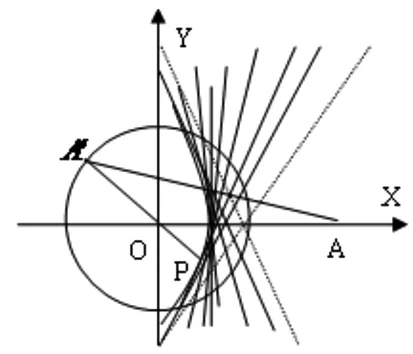
圖9

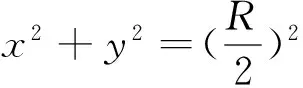
本例通過聯想發散，揭示了折紙模型背后的數量關系，激活了默會知識，得到一般化的數學結論.在邏輯推理核心素養的形成過程中，學生能夠從數學的視角發現問題、提出問題，分析問題，理解數學知識之間的聯系，建構知識框架，形成有論據、有條理、合乎邏輯的思維品質，培養了學生的數學創新能力.

無數實踐證明：“科學的創新根源于默會的力量”，社會和經濟發展的信息化和全球化的趨勢，對人的創新精神培養和創造型人才的成長，提出了前所未有的緊迫要求.研究性學習提倡把知識放到一定的情境中，使書本知識重新被“激活”，使知識恢復到鮮活的狀態，只有這樣的知識，才能激活、喚起學生的內在需要、興趣和信心，才能提升他們主動探求的欲望.由此可見，默會知識的激活對學生的數學學習不可或缺.

[1]王梓坤，科學發現縱橫談[M].北京師范大學出版社，1993年10月第1版.

[2]葉立軍，中學數學教學設計[M].高等教育出版社，2015年6月第1版.

[3]史寧中，數學基本思想18講[M].北京師范大學出版社，2016年10月第1版.