把握函數結構 生成動態認知
——復習課《二次函數的表達方式》案例

季近仁

(江蘇省蘇州工業園區唯亭學校 215000)

一、問題的提出

《二次函數》是蘇科版初中數學九年級下冊第五章的內容，分別從二次函數，二次函數的圖象與性質，二次函數與一元二次方程，二次函數的應用四個方面進行教學.在學習完新課之后，從建構主義和認知主義多元視角解析二次函數，我們發現，略顯干澀的二次函數解析式中可以求出無數個二次函數上的點，通過表格的輔助得到圖象，圖象直觀地描述了二次函數的性質，其中與x軸的交點問題又與一元二次方程契合，另外在現實問題中，往往給出的是表格或者圖象，而不是解析式.綜觀整體，二次函數的教學中暗含了一條隱線：二次函數的三種表達形式之間的相互轉化.基于此，我設計了《二次函數的表達方式》的課堂教學.

二、理論基礎

1.建構主義

建構主義是在皮亞杰的自我建構論和維果斯基的社會建構論的基礎上建立起來的.建構主義者的觀點是學習實質是學習者主動建構內部心理表征的過程，學習結果是知識的網絡結果，學習過程是獨特的，非一致的信息加工活動，自我建構，強調自我探索，協作學習.建構主義的基本思路是：注重以學生為中心進行教學；注重在實際情境中進行教學；注重協作學習，提倡師徒式傳授；注重提供充分的資源，讓學生自我探索.最根本的一點就是建構主義認為知識不是通過教師傳授得到，而是學生主動建構獲得的.

2.認知主義

以布魯納和奧蘇泊爾等為代表的認知主義心理學家提出，學習是學習者內部認知結構的形成和改組.課程目標應能促進學生認知結構的形成和發展，課程設計要一句學生的認知結構水平，尊重認知規律，教材編制要體現“結構”論的思想，在教學過程中應注意提供先行組織者，以便學生的新舊知識與經驗產生聯系.

三、復習課《二次函數的表達方式》案例

本節課的教學目標是掌握二次函數的解析式、表格、圖象三種表達方式以及相互的轉化；分別從二次函數解析式、表格、圖形三個角度認識二次函數的性質；體會數、表、形之間的聯系，感受數學的一般化思想.由于在平時教學中，我們多有強調解析式與圖象，使得學生對于表格的認識停留在解析式與圖象的媒介，因此本節課的教學重難點是從表格中認識二次函數的性質.

教學一開始，復習導入，讓同學們回憶已經學習過的二次函數的三種表達形式，直接點明本節課的主題，為本節復習課打下第一塊基石.

1.首先，從學生最熟悉的解析式入手.

問題1 已知二次函數解析式y=x2-4x+3，你能得到函數的表格和圖象嗎？

x……y……

問題1的提出，揭示了二次函數的解析式，表格，圖象三者之間最原始的關系，既起到了復習的作用，又展示了二次函數的三種表達形式.學生上手比較快，尊重學生的認知水平和認知規律，強化了學生的操作能力，激發學生興趣.

2.其次，我們來研究一下平時有所忽略的表格中蘊含著哪些秘密.

問題2：已知二次函數的表格，

(1)你能從表格中得到哪些關于函數的信息？

x…-4-3-2-1012…y…0-5-8-9-8-50…

①通過觀察得到二次函數的頂點坐標____，對稱軸是____;

②二次函數有最____值，當x=____時，y有最____值____;

③通過觀察得到二次函數與x軸交點為____;

④通過觀察得到二次函數與y軸交點為____;

⑤對稱軸的____側，即____，y隨x增大而____，對稱軸的____側，即____，y隨x增大而____.

(2)你能得到函數的解析式嗎？

問題2第一小問通過直接給出表格，以填空的形式幫助學生發現二次函數表格中的信息.填空的內容全面細致，包括了二次函數的基本性質，都是學生熟悉的知識，學生準確率高，掌握情況較好.表格旁的平面直角坐標系是輔助學生發現信息的，可以由學生自己選擇用或者不用，分層教學，因材施教.第二小問可以采用分組教學的方式，每個小組在討論之后給出自己的方法，既復習了二次函數解析式的三種表示方式(頂點式，交點式，一般式)，又連接起了表格與解析式之間轉化的橋梁.

在完成問題2后，通過一個變式讓大家腦洞大開.

變式：你能將二次函數的表格填寫完整嗎？

x…-5-4-2-1013…y…-14-7-2121-2…

變式的方法很多，學生各顯神通，給出了多種不同的解法，無論是求解解析式代入的方法，還是觀察表格對稱性的方法，只要方法得當，計算不復雜，都給予肯定，大大增強了學生的自信心，發散了學生的思維.

因為表格是本節課的重難點，適當輔以練習是很必要的.

練習：

1.二次函數y=ax2+bx+c(a，b，c為常數，且a≠0)中的x與y的部分對應值如下表：

x…-1013…y…-1353…

(1)對稱軸為____；

(2)開口____，對稱軸的右側，即____，y隨x增大而____；

(3)當x=____時，函數值y=-1.

2.已知二次函數y=ax2+bx+c中，函數y與自變量x的部分對應值如表：則當y<5時，x的取值范圍是____．

x…-10123…y…105212…

練習中的兩個小題緊扣問題2 ，從二次函數表格出發，略略增加難度，提出相關的不等式知識，幫助學生在原有基礎上更進一步，符合最近發展區理論.學生在練習中表現出一定的差異，在學生講解之后，大部分學生能夠理解掌握，完善了二次函數的結構.

3.然后，讓我們回到直觀的圖象，來看看有什么新的發現.

問題3：已知二次函數的圖象，

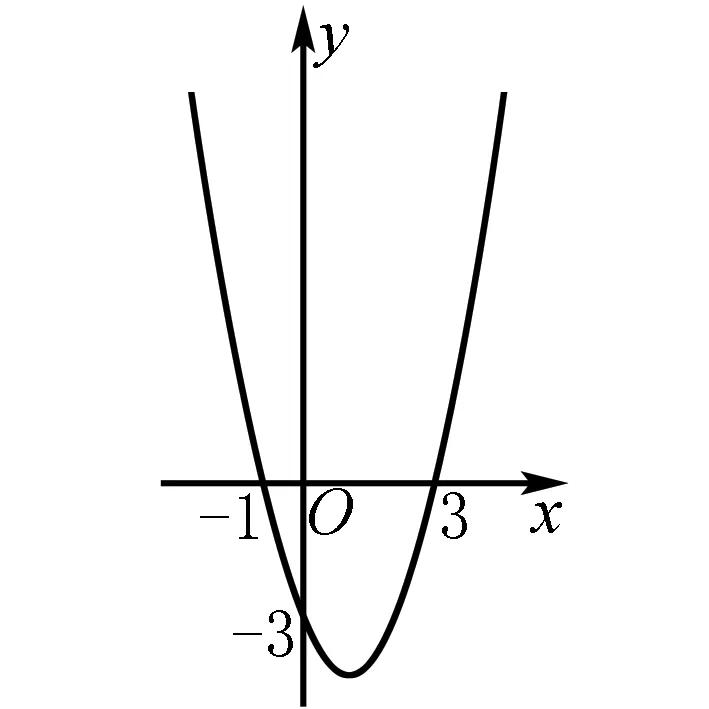
(1)你能從圖象中得到哪些關于函數的信息？

①通過觀察得到二次函數的圖象開口____;

②通過觀察得到二次函數的頂點坐標____，對稱軸是____;

③通過觀察得到二次函數與x軸交點為____;

④通過觀察得到二次函數與y軸交點為____;

⑤二次函數有最____值，當x=____時，y有最____值____.

⑥對稱軸的____側，即____，y隨x增大而____，對稱軸的____側，即____，y隨x增大而____

(2)你能根據函數圖象得到函數的解析式和表格嗎？

類比問題2，觀察圖象得到二次函數的性質，并且從函數圖象回歸函數解析式和表格.幫助學生構建完整的二次函數三種表達形式，透徹理解相互之間的轉化.

通過一組小練習，強化二次函數的圖象.

練習：

1.二次函數y=ax2+bx+c(a≠0)的大致圖象如圖，關于該二次函數，下列說法錯誤的是( ).

A．函數有最小值

B．對稱軸是直線x= 2

C．當x<2，y隨x的增大而減小

D．當10

2.二次函數y=ax2+bx+c(a≠0)的圖象如圖，

(1)補全函數圖象；

(2)求圖象與x軸的交點；

(3)求函數圖象上縱坐標為3的點的坐標.

練習中的兩道題目在熟練掌握問題3后，做起來得心應手，計算強度小，學生產生成就感，感受到了數學的魅力.

4.最后，在掌握的基礎上有所提升，以思考題的形式對本節課進行小結.

(1)寫出該函數圖象的對稱軸；

(2)若將線段OA繞點O逆時針旋轉60°到OA′，

試判斷點A′是否為該函數圖象的頂點？

(3)本節課你有哪些收獲？

學生的收獲可以用圖來表示：

整節課通過新舊知識的聯系，以學生為中心，主動建構新知識，圍繞二次函數的三種表達形式：解析式、表格、圖象，脈絡清晰，注重“結構”教學，學生溫故而知新，從中收獲的不僅是知識，還有興趣，自信，成功的喜悅.

參考文獻：

[1]施良方.課程理論——課程的基礎、原理與問題[M].北京：教育科學出版社，1996.

[2]黃甫全.現代課程與教學論學程[M].北京：人民教育出版社，2006.