基于教學現狀反思有效思維模式的構建

廖凱

[摘 要] 初中學生數學學習水平提升的關鍵在于其思維模式的順利建立，本文在分析現行初中數學教學現狀的基礎上著重闡述了數形思維、化歸思維等模式的有效建構. 教師在日常教學中應注重這些思維模式的教學訓練與引導，使學生能夠掌握轉化或簡化問題的方法并以此提升自己解決問題的能力.

[關鍵詞] 初中數學；思維模式；有效性思維；解決問題；數形結合

教師在初中數學教學中應加強對學生的思維訓練并幫助學生尋求更為有效的思考方式，使得所學內容能夠得到科學的整合與提煉并因此促成學生學習效率的提高.

初中數學教學現狀

1. 重練習，輕方法

教師在以往的數學教學中往往將多做練習題當作提升學生學習能力的主要方式，很多教師認為學生在大量的練習中自然會總結出解題的訣竅并找到最適合自己的學習方式. 事實上，練習確實可以讓學生對公式與概念更加熟悉，學生也能在大量的練習中提升自己的解題速度以及對公式、概念的運用能力. 不過，很多有意義的解題方式卻不是學生在大量機械練習中能夠總結出的，學生一旦遇到稍有變化的復雜問題往往就會束手無策.

2. 重講授，輕歸納

教師在教學中往往比較重視講課的過程且通常還講得比較詳細，這部分教師往往存在“講解越細致，學生掌握知識情況就會越好”的觀點，因此，課堂教學進程相對更加緩慢，導致教師對課堂內容的歸納無法實現. 數學知識中每個章節所包含的知識點都存在一定的聯系. 比如一元二次方程這一章中三個小節的內容之間就存在著緊密的聯系，教師如果能夠在整章知識講授結束之后進行有效的總結，不僅能使學生對課程內容進行有效的回顧，還能使學生對所學知識進行分類與融合，并因此促使學生學會將知識進行整合，解決問題的方法也會因此變得更加多樣而靈活.

如何建立有效性思維模式

1. 數形思維模式

學生在學習比較抽象的數學知識時經常會遇到困難，這些抽象知識往往在生活中很難找出其原型，因此，想象成為學生解決此類問題時唯一可以借助的手段. 一旦此類問題比較復雜，學生解題時就很難找出解題的突破口，會顯得更加毫無頭緒，想象與公式的輔助對于解題來說顯得蒼白而無力. 此時，教師如果能夠幫助學生建立數形結合的思維模型，問題往往會因為直觀圖形的存在而變得更加簡潔明了. 教師引導學生根據題意作圖并對圖形展開觀察與探索，一些題目中沒有明確表述的條件很有可能會在直觀的圖解中得到展露. 將這些隱含的條件徹底挖掘并將之與題中已知條件結合，解題的突破口也就很容易尋得了.

例如，已知y=（2-n）x+n的圖像經過第一、二、四象限，求n的取值范圍.

題目對作圖并沒有提出明確的要求，但此題如果不作圖，求解的過程還是非常有難度的. 因此，教師應該引導學生根據題意進行作圖，直觀的圖像與已學的公式相結合很快令學生獲得答案. 繪圖在解決數學問題的過程中所起的作用顯而易見，因此，教師在日常教學中應經常引導學生養成繪圖來解決問題的習慣. 繪圖這一直觀的解題手段在函數、方程等多個知識模塊中都有很好的應用. 利用圖形解題在幾何這一知識體系中的應用是最為廣泛的，根據題意首先作圖，然后再添加輔助線等進行解題往往能起到事半功倍的效果. 因此，教師引導、幫助學生建立數形結合思維模式對于學生的數學學習以及能力提高來說都是極具價值的.

2. 樸素思維模式

初中數學中有些題目還是相當有難度的，特別是試卷中的壓軸題，往往令學生束手無策，數學基礎較差的學生甚至連題目所表達的意思都無法理解，很多學生因此果斷放棄了這部分題. 這部分復雜問題究竟應該如何突破或將其簡單化呢？筆者以為建立樸素思維應該是極為有效的. 例如，筆者先前在動態問題的歸類上是這樣歸納的：動態全等三角形、動態相似三角形、動態等腰三角形、動態直角三角形、動態圓等；單動點、雙動點等. 學生并沒有因為這樣的分類而獲得更好的學習效果. 筆者針對學生的學習情況以及動態問題的思考重新進行了分析. 首先將題中的靜態部分進行了分析，然后引導學生結合自身認知對動態問題形成思考，這樣的樸素思維使得學生的學習效果增強了很多.

再比如，近年來中考壓軸題的命題很多都著眼于對稱點的求解，那么，一般性對稱點的求解方法我們又應如何思考呢？

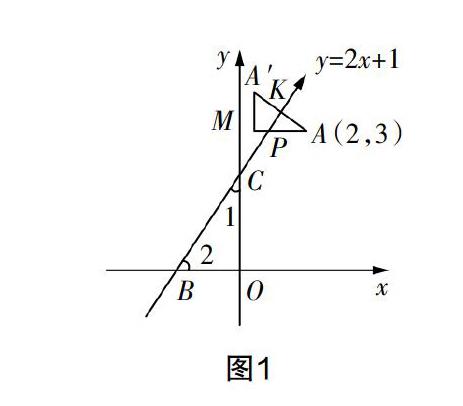
例如，如圖1所示，求點A（2，3）關于直線y=2x+1的對稱點A′的坐標.

3. 化歸思維模式

大多教師在教學中很少提及化歸思想，主要因為學生對化歸思想的概念與應用都不甚清楚. 但事實上，化歸思維模式往往能將題中的問題進行轉化并因此使問題得以簡化. 化歸思維模式如果能夠順利建立，必然能令學生在問題的探尋中找到關鍵之處并進行轉化. 因此，教師在教學中應把探尋題中關鍵點的方法教給學生，使學生在分析題目時能明確可以轉化的問題以及轉化的條件，最后再設計出適量而科學的練習使學生能夠熟練掌握這些方法.

例如，四邊形課程的講授之后往往會安排一定的練習題，某一例題如下：已知一道路形狀如圖2所示，其橫向、縱向長度分別為8 m、7 m，寬為1 m，如果按照箭頭方向與位置行走至中間箭頭所指位置，則一共走過了多少米？

大多學生在解此題時都根據題目描繪的意思進行了路線的繪制，然后再將一段一段的路線求解出來進行相加而求得最后的答案. 這樣的計算因為各段橫向與縱向長度的求解而呈現出巨大的計算量，而且，很多學生在求解之時往往將自己也繞了進去，所以很多學生的結果都錯了. 但如果運用化歸的思維方式設計一個保潔工人拖地的情境，此題就會變得簡便許多. 假設保潔工人拖地時的拖把寬度為1 m，當他走到終點時就意味著這一圖形道路已被全部走完，因此計算出道路的面積再除以寬度1 m就能求出道路的長度了，這一方法不僅簡便還不易出錯.

4. 分類思維模式

很多數學知識之間都會存在一定的聯系與相似性，學生在這些知識的學習中常常容易產生混亂. 因此，在此類知識的學習中建立分類的思維模式是很有必要的，所學知識經過分類與總結能夠使學生有效避免學習中的混亂. 在具體解題中，學生面對一些條件較多的復雜題型往往會對條件的使用產生混亂，學生在解題時一旦用亂條件，錯誤隨即產生. 因此，教師在教學中應引導學生對條件進行區分并按照線索將其進行分類.

例如，A，B兩城分別有肥料200噸和300噸，現在準備將A，B兩城所有的肥料運往C，D兩鄉，已知從A城運肥料到C，D兩鄉的費用分別是20元/噸和25元/噸，從B城運肥料到C，D兩鄉的費用分別是15元/噸和24元/噸，現C，D兩鄉各需要肥料240噸和260噸，怎樣調運才能最節約運費？

像這樣的題目條件眾多，教師應引導學生在審題時進行畫圖分類. 必要的時候帶上單位一起進行分析，題中條件以及條件之間的關系才能得到最好的梳理并順利求得答案.

結束語

初中生數學學習水平提升的關鍵正是其思維模式的建立，本文所闡述的數形、樸素、化歸、分類等思維模式在初中數學學習的過程中是極為有效的. 教師在日常教學中應注重這四種思維模式的教學訓練與引導，使學生能夠掌握轉化或簡化問題的方法并以此提升自己解決問題的能力.