關聯前后：中考一輪復習的用力點
——由“一次函數的再認識”說起

☉江蘇靖江外國語學校 丁曉艷

最近，我們在某微信公眾號看到一份“一次函數的再認識”的復習資料，作者指出：對一種事物從不同角度認識它，用不同的方法分析它，我們對它的理解就越來越深刻，就更容易領悟它的本質，并能感受事物之間的聯系與統一.并且把一次函數與諸多數學知識進行了聯系，大開眼界，筆者以為，值得我們在中考一輪復習時適當引用.下面就先摘引相關觀點，并跟進教學思考，供研討.

一、一次函數的再認識

再認識之一：一次函數與三角函數.

1.如圖1，斜坡AB的坡度i為1：2.坡度是指傾斜程度，它還與傾斜角∠B的大小有關，等于∠B的正切值，或斜邊所在的垂直高度與水平長度的比.

圖2

圖1

2.如圖2，直線y＝kx＋b中k的幾何意義：k代表直線的傾斜程度.

可見，既然都是傾斜程度，圖2中的k與∠ABO的正切（AO∶BO）恰等于坡度i.它們是一回事！k為正時是上坡，k為負時是下坡.

再認識之二：一次函數與等差數列.

我們知道，數列3，7，11，15，19，…，第n項表達式是a＝3＋4（n－1）.

顯然，數列的項a與項數n的關系式為a＝3＋4（n－1），整理為a＝4n－1，可見a與n的關系是一次函數關系（可用圖3來表示數列），其k值就是公差.當k為正時遞增，當k為負時遞減.

圖3

再認識之三：k與速度（單價、工作效率等）的關系.

如圖4，表示行駛路程y（km）與行駛時間t（h）的關系，AB段的速度是60km/h，AB段對應的一次函數關系式中的k恰為60.

可以發現：k值即是速度.同理，在金額與數量的函數關系中，單價就是k值，在工程問題中，工作效率就是k值.

認識到這一點之后，我們可以直接寫出AB段的函數關系式，比如，y＝80＋60（x－1），y＝80－60（1－x），y＝260－60（4－x），y＝260＋60（x－4），整理之后都是y＝60x＋20（1≤x≤4）.

再認識之四：一次函數、等差數列、坡度、正切、速度（單價、工作效率等）的聯系.

現在我們把以上圖形中的兩個量的比值在圖5～圖8中標注出來，對比觀察一次函數的k值、等差數列的公差、坡度、正切、速度、單價的共同點.

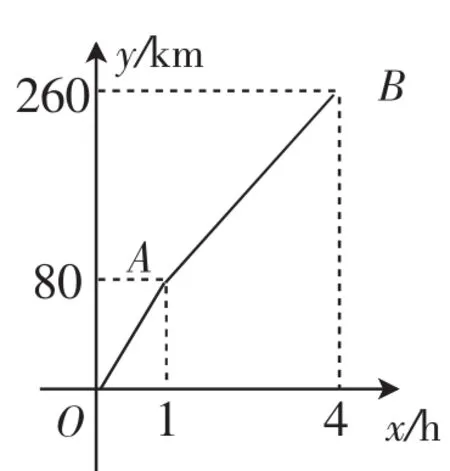
圖4

圖5

圖6

圖8

可見，它們的共同點：都是兩個量的比值.這種比值還有另一種意義：單位增量.具體來說，速度為k千米/小時的意義是：時間每增加1小時，所行的路程就增加k千米.

單價為k元/千克的意義是：數量每增加1千克，商品的金額就增加k元.

坡度為k的意義是：斜坡的水平距離每增加1千米，對應的垂直高度就增加k千米.

公差為k的意義是：數列的項數每增加1，項的值就增加k.

一次函數k的意義是：x值每增加1個單位，對應的y值就增加k個單位.

可見，一次函數是對上述實際問題的抽象和概括.它的本質特征是定比，即每一段函數對應的函數值y的變化量與自變量x的變化量的比值一定.

再認識之五：一次函數表達式的多樣解法.

例1如圖9，求直線AB的函數關系式.

分析：初中教材介紹的多是待定系數法，略去不說，這里再介紹一種算術方法列式計算.

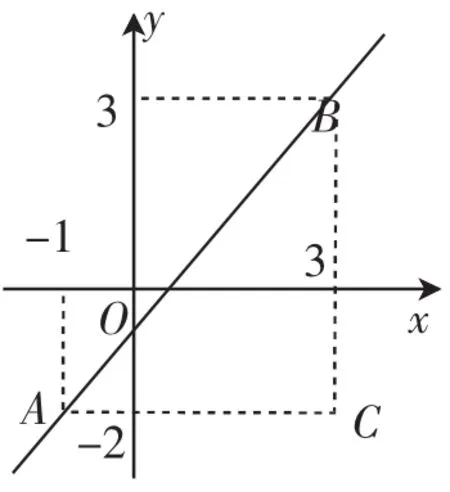
圖9

例2某公司以30元/千克的價格收購一批農產品進行銷售，為了得到日銷售量p（千克）與銷售價格x（元/千克）之間的關系，經過市場調查獲得部分數據，如下表：

售價x/（元/千克） 30 35 40 45 50日銷量p/千克 600 450 300 150 0

請根據表中的數據，用所學過的一次函數、二次函數、反比例函數的知識確定p與x之間的函數表達式.

分析：當x成等差數列時，y值也是等差數列，符合一次函數特征.可以設y＝kx＋b，用待定系數法列二元一次方程組確定k、b的值.

例3一輛慢車從甲地勻速行駛至乙地，一輛快車同時從乙地出發勻速行駛至甲地，兩車之間的距離y（千米）與行駛時間x（小時）的對應關系如圖10所示：

圖11

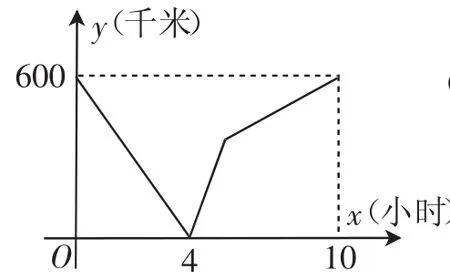
圖10

分析：解答這道經典考題的關鍵是各個折線段的函數關系式，簡示如圖11.

二、關于中考一輪知識點復習的教學思考

1.一輪復習時知識點的梳理要注意跨年級關聯整合.

當前很多中考一輪復習的學案或教輔資料中，總是限于某一個單元的知識點進行知識梳理或性質回顧，比如，對于一次函數，在中考一輪復習時，常常與八年級單元復習無甚區別，這種“無差別”的復習課備課思路，屬于辨識年級復習重點不清的表現.從上文中梳理的一次函數的再認識來看，就不僅僅滿足于八年級學習一次函數的一些知識點與性質，而是打破年級的界限，關聯、溝通了一次函數、正切函數、等差數列（初中沒有系統學習，但是在很多規律問題中非常多見）、行程與工程等應用問題，值得借鑒.

2.一輪復習時例、習題的講評要選用不同算法或證法.

一輪復習側重基礎知識的梳理、基本方法的回顧，還有經典問題的快速與精準解答，所以一輪復習往往會精選一些此前學生在新授課階段已反復練習過的一些典型問題（往往也是必考題型），這時就不能只是滿足于一種解法或核對答案，怎樣做到“老歌新唱”？筆者以為，像上文例題部分從不同角度來求解一次函數的解析式就是一種值得學習的方式，因為到了中考復習階段，絕大多數學生對待定系數法已經非常熟練，如果再練一次待定系數法，只是增加熟練程度，而能夠引入另外的方法（有時讓學生來展示他們獨特的解法也是值得注意的），可以開拓學生的解法視角，讓他們知道“殊途同歸”，掌握不同方法解決經典問題可以進行解法之間的“校正”，以免一種方法求解時出現筆誤等低級失誤.

3.一輪復習時要注意引導學生用“高觀點”回看舊知.

一輪復習側重基礎知識，怎樣把這些基礎知識納入到高觀點來加以理解，讓零散的知識點“串珠成線”是中考復習的追求.像上文這樣，把一次函數的一次項系數k從更廣泛的背景下進行關聯理解，深刻理解一次函數作為一種數學模型的重要性.這樣的案例還有很多，如七、八級很多分析代數式的最值問題，可以從二次函數最值的“高觀點”來思考，一元二次方程根的判別式問題，可以結合二次函數的圖像與直線交點問題“高觀點”來思考，直線型幾何很多邊、角的關系，包括一些輔助線的添加等，都可以從圓的“高觀點”來思考.

三、寫在后面

中考一輪、二輪復習側重于知識點和題型復習是很多地方形成的“教學慣習”，然而怎樣基于考情、學情，進一步重組復習內容，聚焦考查重點、熱點與難點，仍然值得我們深入思考.本文由一篇網絡傳播的公眾號文章說起，分享其對我們的一些啟示，特別是基于高觀點的理解與認識，值得大家傾聽和研習.當然，我們的解讀、賞析還是很初步的，期待更多的批評與指正.

參考文獻：

1.劉東升.關聯性：一個值得重視的研究領域［J］.中學數學（下），2013（12）.

2.張玉萍.把問題作為教學的出發點——由曹才翰先生的一篇評課文獻說起［J］.中學數學（下），2016（12）.

3.鮑建生，顧冷沅等，變式教學研究［J］.數學教學，2003（1、2、3）.