基于優效課堂的數學概念課的課堂評價*
——以“函數的單調性”新授課的評價為例

☉廣東省廣州市第八十六中學 胡革新

如何評價課堂教學質量，是值得研究的問題.高中數學概念課的課堂評價，基于高中數學“優效課堂”的基本觀點、基本特征、教學策略、好課味道和好課標準［1-5］，旨在建構數學概念課的課堂評價量表.

筆者認為，高中數學概念課的課堂評價，要體現數學概念課的課型特點，既要關注教師的課堂教學行為，又要重視學生的課堂學習過程；通過課堂評價，促進學生數學學科核心素養的發展，幫助教師改進教學.下面以“函數的單調性”的課堂評價為例，與同行分享.

一、高中數學概念課的評價依據

1.高中數學“優效課堂”的基本觀點

高中數學“優效課堂”要“為核心素養而教”、“以理性思維育人”，要彰顯數學的思維方式、洋溢數學的味道.高中數學“優效課堂”追求“負擔輕、效率高、效益佳、質量優”，要求教師在遵循教學規律與學生認知規律的基礎上，實施“優效教學”，促進學生“優效數學學習”，在適度的時間和精力投入后實現課堂教學目標，促進學生數學核心素養的發展.

2.高中數學“優效課堂”的基本特征

基于核心素養的高中數學“優效課堂”的基本特征是：核心素養引領下的教學目標設置，教學策略的適切化，教學過程的最優化，課堂評價的多元化.

3.高中數學“優效課堂”的教學策略

高中數學“優效課堂”的教學策略有：目標定向、面向全體、問題驅動、過程展示、變式探究、方法提煉、文化熏陶.

4.高中數學“優效課堂”的好課味道

高中數學“優效課堂”的好課有三種味道：數學味、文化味和藝術味.數學味是指數學課要展現“數學化”過程、以數學的方式育人，其本質是數學化.文化味是指數學課要發揮數學的內在力量，體現數學的文化價值，以數學的理性思維育人，其本質是理性思維.藝術味是指數學課要講究教學藝術，既要獲得數學“四基”又要展現“再創造”過程，形成情感體驗，其本質在于創新.

5.高中數學“優效課堂”的好課標準

（1）教學目標明確具體、動態生成、適宜測評.

（2）教學策略能有效促進學生的優效數學學習.

（3）教學活動合理有序、關注個性、講究效率.

（4）學習活動狀態優良、參與充分、注重創新.

二、高中數學概念課的評價量表

1.高中數學概念課的課型特征

數學概念課是以獲得概念為主的課型.數學概念因客觀現實或數學自身發展的需要而產生，是數學思維的基本形式，是反映空間形式和數量關系的本質屬性的理性認識.從概念學習的心理角度來看，數學概念具有抽象性、多元性、層次性和系統性等基本特征.從教學過程來看，數學概念教學包括概念的引入、概念的明確與理解、概念的鞏固和運用等三個階段，因此數學概念課的一般教學結構是：引入概念—理解概念—運用概念—反思提煉.

（1）教學目標.數學概念課的主要教學目標是幫助學生獲得數學概念，并在概念學習過程中形成抽象概括能力、理解數學方法、領悟數學思想、感受數學文化.

（2）教學要求.數學概念教學要引導學生經歷概念學習過程，理解數學概念的本質，把握概念中蘊含的數學思想方法，著力培養學生的數學學科核心素養.數學概念教學的一般要求是：通過概念的引入，讓學生認識概念的來龍去脈；通過概念的明確，讓學生掌握概念的內涵和外延，掌握概念的名稱、定義、示例、屬性、符號表示等；通過概念的運用，讓學生建構相關數學概念的聯系.數學概念教學要注重變式，在變式中掌握概念的本質.［6］

（3）教學策略.概念形成與概念同化是掌握概念的兩種基本教學策略.概念形成是由概念原型概括出新概念.概念同化是由已有概念獲得新概念，直接用數學語言給出數學概念.也可用概念形成與概念同化相結合的方式獲得數學概念.在數學概念教學中，宜將概念形成與概念同化相結合，以促進學生對數學概念的理解.

2.高中數學概念課的課堂評價量表

依據高中數學概念課的課型特征，基于高中數學“優效課堂”的基本觀點、基本特征、教學策略、好課味道和好課標準，我們構建出如下高中數學概念課的課堂評價表（表1）.

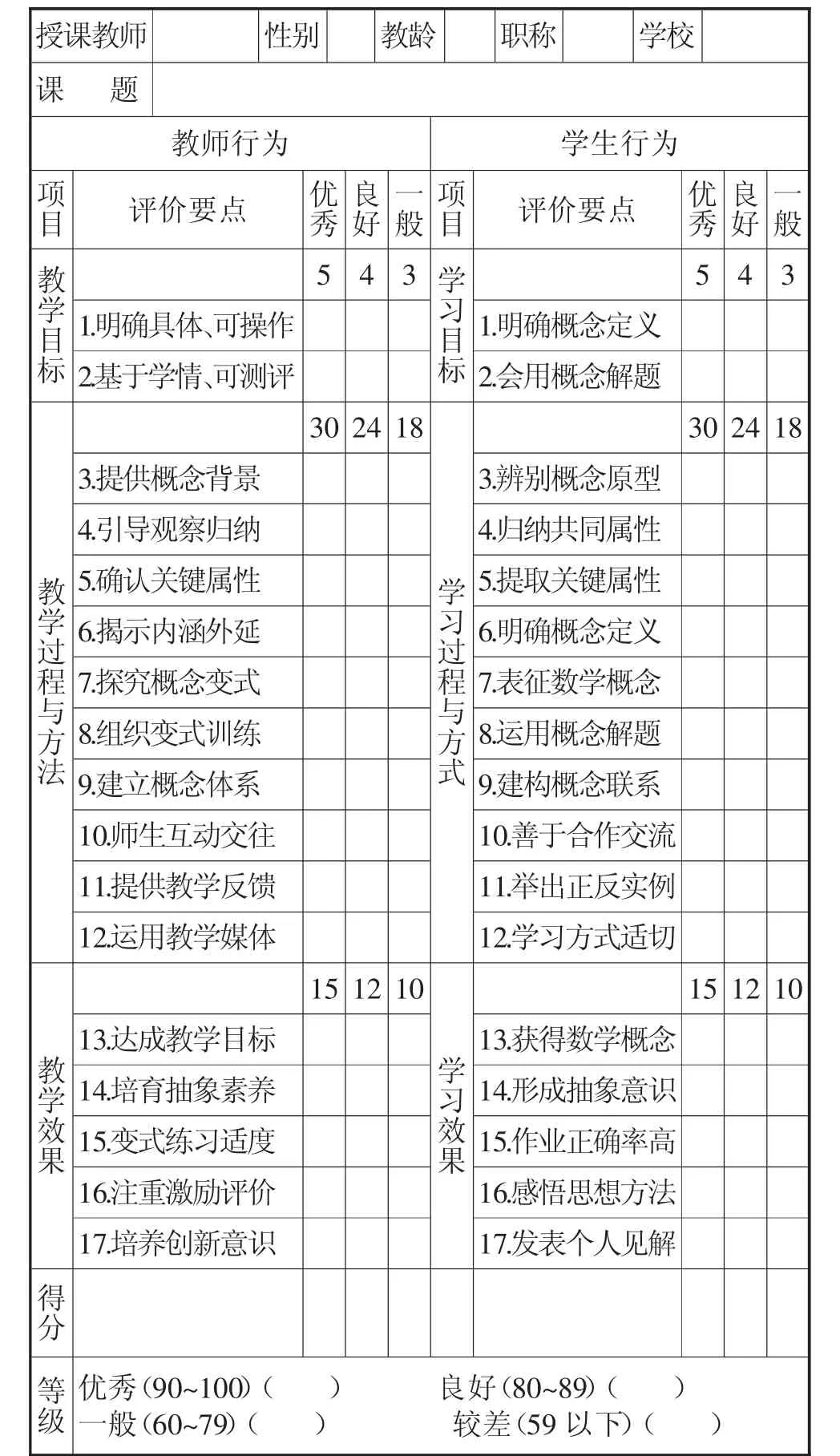
表1 高中數學概念課的課堂評價表

說明：從教師行為、學生行為兩個維度進行量化評價（各50分，滿分100分），每個維度又分三個一級指標（目標占5分、過程占30分、效果占15分），每個一級指標又分為幾個二級指標（評價要點），共17個二級指標，每個二級指標占3分（其中第2個二級指標占2分），評價要點中優秀、良好、一般所賦分值均為該等級上限.

三、高中數學概念課的評價案例

下面以“函數的單調性”新授課為例，呈現高中數學概念課的評價實踐.

1.課堂實錄

上課伊始，教師導入新授概念（問題1）.

問題1：觀察函數f（x）=x+1、f（x）=-x+1、f（x）=x2+1的圖像，從左到右看，函數f（x）有何圖像特征？函數f（x）隨x增大如何的變化？

學生1：從左到右看，函數f（x）=x+1的圖像呈“上升”趨勢，函數f（x）隨x增大而增大.

學生2：從左到右看，函數f（x）=-x+1的圖像呈“下降”趨勢，函數f（x）隨x增大而減小.

學生3：從左到右看，函數f（x）=x2+1的圖像在區間（-∞，0）上呈“下降”趨勢，函數f（x）隨x增大而減小；在區間（0，+∞）上呈“上升”趨勢，函數f（x）隨x增大而增大.

在學生回答基礎上，教師給出增函數、減函數的名稱（圖形語言）：

在數學中，通常把“圖像從左向右呈上升趨勢”的函數稱為增函數，而把“圖像從左向右呈下降趨勢”的函數稱為減函數.

接下來，教師引導學生建構概念定義（問題2）.

問題2：依據函數圖像的“上升”“下降”趨勢，如何定義增函數、減函數呢？

學生4：若函數f（x）隨x的增大而增大，則稱f（x）為增函數.

學生5：若函數f（x）隨x的增大而減小，則稱f（x）為減函數.

緊接著，教師呈現問題3.

問題3：如果將“f（x）隨x的增大而增大”作為增函數的定義，能用定義證明函數f（x）=x2+1在區間（0，+∞）上是增函數嗎？

學生：這樣的定義，沒法運算與推理.

接下來，教師呈現問題4.

問題4：如何定量刻畫二次函數f（x）=x2+1“在區間（0，+∞）上，f（x）隨x的增大而增大”？能列舉一些具體數據嗎？

學生6：f（1）=2，f（2）=5，f（1）＜f（2）.

學生7：f（2）=5，f（3）=10，f（2）＜f（3）.

教師追問：這樣的列舉能刻畫增函數的本質嗎？用什么辦法來定量刻畫呢？

眾生：不知道如何定量刻畫f（x）隨x的增大而增大.

教師引導：

①“增大”意味著比較，需要建立兩個量的大小關系；

②“x的增大”的符號化：用兩個自變量的大小關系表述為x1＜x2；

③“f（x）增大”的符號化：f（x1）＜f（x2）；

④“隨”字的符號化：當x1＜x2時，有f（x1）＜f（x2）；

⑤“在區間（0，+∞）上，f（x）隨x的增大而增大”的符號化：對任意的兩個自變量x1，x2∈（0，+∞），當x1＜x2時，都有f（x1）＜f（x2）.

這樣的定量刻畫方式就可進行運算與推理了.

接下來，教師呈現問題5.

問題5：若函數f（x）在定義域I內某個區間的圖像如圖1所示，能用符號語言來表示函數f（x）的變化趨勢嗎？

圖1

在學生嘗試基礎上，教師給出函數單調性的形式化定義：

一般地，如果函數f（x）對于定義域I內某個區間D上的任意兩個自變量x1，x2∈D，當x1＜x2時，都有f（x1）＜f（x2），則稱函數f（x）在區間D上是增函數.

如果函數f（x）對于定義域I內某個區間D上的任意兩個自變量x1，x2∈D，當x1＜x2時，都有f（x1）＞f（x2），則稱函數f（x）在區間D上是減函數.

如果函數f（x）在區間D上是增函數或減函數，則稱函數f（x）在這一區間上具有（嚴格的）單調性，區間D叫做y=f（x）的單調區間.

教師強調：上述定義中包含區間、任意、增函數、減函數、單調區間等5個關鍵詞.

在獲得增函數、減函數的概念后，教師組織變式訓練（問題6）.問題6：證明函數在區間（0，+∞）上是減函數.

生眾：運用減函數定義解題（過程從略）.

教師規范推理過程后，引導學生變式訓練：

變式1：證明函數在區間（-∞，0）上是減函數.

變式2：函數在定義域I上的單調性是怎樣的？證明你的結論.

變式3：證明函數（f x）=x2+1在區間（0，+∞）上是增函數.

變式4：證明函數在區間［1，+∞）上是增函數.

接下來，教師呈現問題7.

問題7：函數y=（x-1）2在區間（-∞，+∞）上是增函數嗎？請說明理由.

學生積極思考，合作交流，得出問題7的答案.

接下來，教師引導學生探究概念變式（問題8和問題9）.

問題8：如果函數f（x）對于定義域I內某個區間D上的任意兩個自變量x1，x2∈D，當x1＜x2時，都有f（x1）-f（x2）＜0，函數f（x）在區間D上是增函數嗎？

問題9：如果函數f（x）對于定義域I內某個區間D上的任意兩個自變量x1，x2∈D，當x1＜x2時，都有f（x1）-f（x2）＞0，函數f（x）在區間D上是減函數嗎？

生眾：思考問題8和問題9的答案.

學生8：如果函數f（x）對于定義域I內某個區間D上的任意兩個自變量x1，x2∈D，當x1≠x2時，（x1-x2）［f（x1）-f（x2）］＞0，則函數f（x）在區間D上是增函數.

學生9：如果函數f（x）對于定義域I內某個區間D上的任意兩個自變量x1，x2∈D，當x1≠x2時函數f（x）在區間D上是增函數.

教師：很好！這兩位同學善于創新.

下課時間臨近，教師引導學生反思（問題10）.

問題10：回顧上述學習過程，有何感悟？

學生反思函數單調性的學習過程，概括出定義法證明單調性的操作步驟：取值定序—作差變形—判斷符號—給出結論.

教師布置課外作業后，結束了本節課.

2.評價記錄

（1）對教學目標與學習目標的量化評價.

通過查閱教學設計、觀察課堂表現，教學目標定位準確，學習目標清晰，評定為10分.

（2）對教學過程與學習過程的量化評價.

從教學過程來看，教師提供概念背景、引導觀察歸納、揭示內涵外延、探究概念變式、組織變式訓練、提供教學反饋；從學習過程來看，學生提取關鍵屬性、明確概念定義、表征數學概念、運用概念解題、舉出正反實例.問題1引導學生觀察三個具體函數的圖像“上升”“下降”特征，學生明白不同函數有不同的圖像特征；問題2引領學生描述函數圖像“上升”“下降”的變化趨勢，學生給出增函數、減函數的描述性定義；問題3引起認知沖突，學生體驗到形式化定義的必要性；問題4從定量刻畫入手，學生感悟到定量刻畫函數f（x）=x2+1在區間（0，+∞）上隨x的增大而增大的方法；問題5搭建腳手架，引領學生獲得增函數、減函數的形式化定義；問題6提供運用增函數和減函數定義的教學情境，通過4個變式來強化定義的正向運用，學生理解單調性概念，培養了邏輯推理素養；問題7通過反例變式，深化學生的概念理解，培養了學生的批判性思維品質；問題8、問題9創設探究概念變式的教學情境，引領學生提出新觀點、新命題，培養了學生的創新意識；問題10關注數學活動經驗的積累，有利于培養學生的元認知能力.

總之，教師著力于問題驅動、建構函數單調性概念，學生經歷圖形語言、文字語言向符號語言轉換的過程，體會到從具體到抽象、從定性到定量的研究方法.但教學媒體運用不夠，學習方式較為單一，因此，教學過程與學習過程的量化評價為54分.

（3）對教學效果與學習效果的量化評價.

從教學效果與學習效果來看，教學目標達成良好，獲得單調性概念.教師注重培養抽象素養和創新意識，變式練習適度，注重激勵評價；學生形成抽象意識，感悟思想方法，作業正確率較高，發表個人見解.因此，在教學效果與學習效果的量化評價中，評定為28分.

綜上所述，總分評定為92分，評定等級為優秀.

課堂評價，難度較大.不同的教學理念，有不同的課堂評價標準.在數學核心素養引領下，高中數學概念課的課堂評價值得深入探究.

1.肖凌戇.高中數學“優效課堂”的理論建構［J］.中國數學教育（高中版），2015（12）.

2.肖凌戇.數學教學要“為思維而教”［J］.中學數學教學參考（上旬），2016（1/2）.

3.肖凌戇.基于核心素養的高中數學優效課堂的基本特征［J］.中國數學教育（高中版），2017（12）.

4.胡革新，肖凌戇.高中數學優效課堂的好課味道［J］.中國數學教育（高中版），2018（3）.

5.肖凌戇，張先龍.高中數學“優效課堂”研究［M］.西安：陜西師范大學出版總社，2017.

6.肖凌戇.從被動接受學習走向變式創新學習——中學數學變式創新學習模式的探索［J］.中學數學，2003（10）.F