課堂意外是培養(yǎng)學(xué)生數(shù)學(xué)核心素養(yǎng)的絕佳時(shí)機(jī)
——以一堂函數(shù)圖像的探究課為例

☉浙江省寧波市北侖中學(xué) 毛浙東

自從高中課標(biāo)修訂組提煉出六個(gè)數(shù)學(xué)學(xué)科核心素養(yǎng)“數(shù)學(xué)抽象、邏輯推理、數(shù)學(xué)建模、數(shù)學(xué)運(yùn)算、直觀想象、數(shù)據(jù)分析”以來，我們廣大的一線教師積極響應(yīng)，在課堂教學(xué)設(shè)計(jì)中，融入了很多核心素養(yǎng)的元素，這是令人欣喜的.

記得章建躍先生曾說：“數(shù)學(xué)課改的核心任務(wù)是提升學(xué)生的數(shù)學(xué)學(xué)科核心素養(yǎng)，要把數(shù)學(xué)學(xué)科核心素養(yǎng)的培育落實(shí)在數(shù)學(xué)教育的各個(gè)環(huán)節(jié).”王尚志教授也指出：“培養(yǎng)并提升核心素養(yǎng)，需要理解、感悟，需要主動(dòng)、自覺地將‘學(xué)生為本’的理念與教學(xué)實(shí)際有機(jī)結(jié)合.”

既然要將核心素養(yǎng)的培育落實(shí)到教育的各個(gè)環(huán)節(jié)，那我們不能只把目光集中在課堂預(yù)設(shè)中；既然我們要主動(dòng)、自覺，將“學(xué)生為本”的理念與教學(xué)實(shí)際有機(jī)結(jié)合，我們就應(yīng)該更多地關(guān)注課堂中的意外生成.

其實(shí)，課堂意外正是培養(yǎng)學(xué)生核心素養(yǎng)的絕佳時(shí)機(jī).下面，筆者就以自己執(zhí)教的一堂函數(shù)圖像的探究課為例，來與各位同行一起探討一下，如何在課堂意外中捕捉培養(yǎng)學(xué)生核心素養(yǎng)的機(jī)會(huì)，希望能拋磚引玉.

一、課堂實(shí)錄

（一）踏破鐵鞋無覓處——課堂意外，喜得方法

師：我們今天來探究形如的函數(shù)的圖像和性質(zhì).下面我們先來研究特殊情形：即研究函數(shù)的圖像與性質(zhì).

當(dāng)筆者利用描點(diǎn)法畫出了圖1，并想繼續(xù)往下講解時(shí)，忽然聽到學(xué)生1的笑聲.

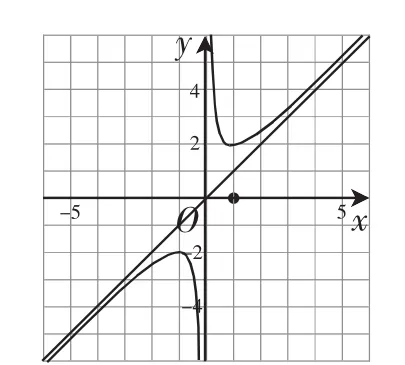
圖1

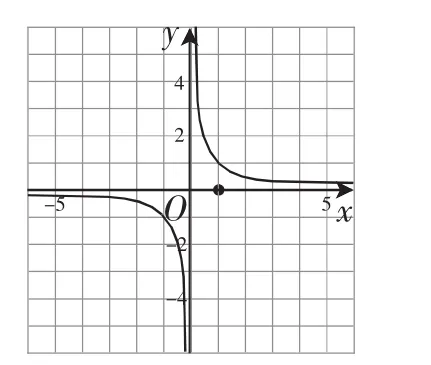
圖2

筆者估計(jì)生1可能發(fā)現(xiàn)了什么，便示意他起身回答.

生1：這不是被擠扁了的反比例函

師：你挺有想象力嘛，不過今天我們研究的這個(gè)函數(shù)叫做“對(duì)勾函數(shù)”，和反比例函數(shù)還是有所區(qū)別的.

生1：沒什么區(qū)別啊，就是被擠壓后的反比例函數(shù)嘛.

筆者一聽來了興致，便繼續(xù)追問.

師：那你說說看，它是怎樣被擠壓的呢？

生1：函數(shù)在平面直角坐標(biāo)系xOy中的圖像如圖2所示.如果將x軸逆時(shí)針旋轉(zhuǎn)45°，即將平面直角坐標(biāo)系xOy擠壓變形得到新的坐標(biāo)系x′Oy.那么在新坐標(biāo)系中，函數(shù)的圖像其實(shí)就是原坐標(biāo)系xOy中的函數(shù)y=.也就是說，要得到函數(shù)的圖像，只需先畫出函數(shù)y的圖像，然后把x軸逆時(shí)針旋轉(zhuǎn)45°，跟著被擠壓變形的函數(shù)的圖像就是的圖像.

（二）莫畏浮云遮望眼——適時(shí)引導(dǎo)，摸索規(guī)律

師：這位同學(xué)旋轉(zhuǎn)坐標(biāo)軸的方法倒是蠻有創(chuàng)意，剛剛他將x軸逆時(shí)針旋轉(zhuǎn)了45°，那如果我們將x軸順時(shí)針旋轉(zhuǎn)45°，又會(huì)得到什么結(jié)論呢？

在教師的啟發(fā)下，學(xué)生展開了探究，不一會(huì)就有學(xué)生舉手.

生2：我按照生1的方法，先作出函數(shù)的圖像，將x軸按順時(shí)針旋轉(zhuǎn)45°，得到新坐標(biāo)系x′Oy，則在新坐標(biāo)系中原函數(shù)的圖像被拉伸成了新函數(shù)，其圖像如圖3所示，它恰好就是函數(shù)的圖像.

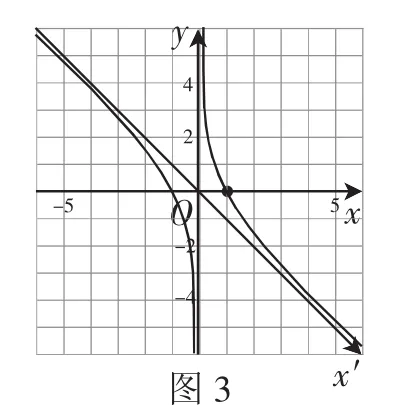
圖3

師：很好，對(duì)于原函數(shù)，若將x軸按照逆時(shí)針旋轉(zhuǎn)45°，就能得到的圖像，將x軸按照順時(shí)針旋轉(zhuǎn)45°，就能得到的圖像.那我們?nèi)绻麑⒃瘮?shù)改變一下，比如改成，那剛才的旋轉(zhuǎn)作圖是否還有效呢？

生3：如果將x軸逆時(shí)針旋轉(zhuǎn)45°，被拉伸后的函數(shù)y=的圖像就是原坐標(biāo)系xOy中的函數(shù)的圖像，如圖4所示；如果將x軸順時(shí)針旋轉(zhuǎn)45°，跟著被擠壓后的函數(shù)的圖像就是原坐標(biāo)系xOy中的函數(shù)的圖像，如圖5所示.

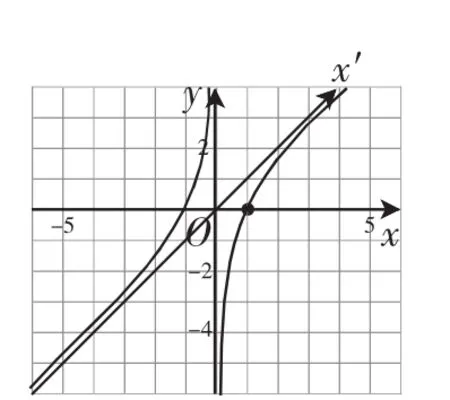
圖4

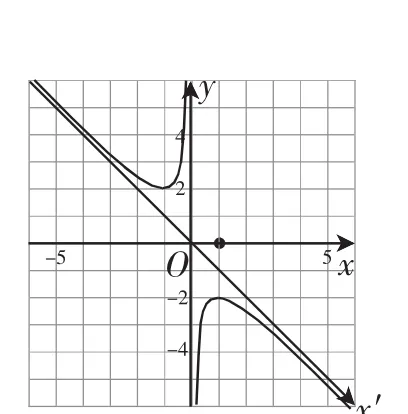
圖5

師：很好，看來改變?cè)瘮?shù)的解析式，這種旋轉(zhuǎn)的規(guī)律依然適用，現(xiàn)在不妨換一個(gè)角度，我們每次是否只能旋轉(zhuǎn)45°，比如旋轉(zhuǎn)30°行不行呢？大家不妨探究一下.

生4：對(duì)原函數(shù)將x軸逆時(shí)針旋轉(zhuǎn)30°，被擠壓后的函數(shù)的圖像就是在原坐標(biāo)系xOy中的函數(shù)y=的圖像，如圖6所示.同理，將x軸順時(shí)針旋轉(zhuǎn)30°，被拉伸后的函數(shù)圖像就是在原坐標(biāo)系xOy中的的圖像，如圖7所示.

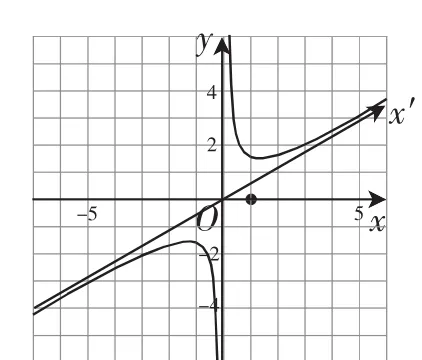
圖6

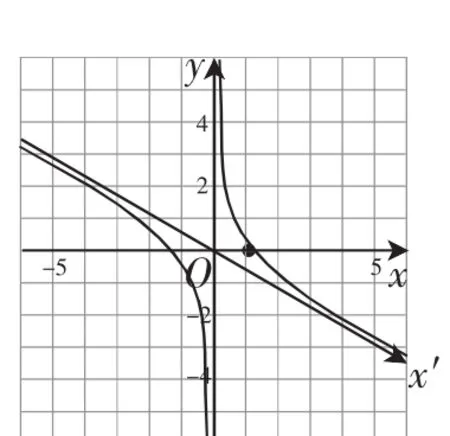
圖7

師：你能夠驗(yàn)證剛才的猜想嗎？

生4：利用計(jì)算機(jī)畫出函數(shù)與函數(shù)y=的圖像，我們發(fā)現(xiàn)恰好是函的圖像的漸近線，這可以說明將x軸逆時(shí)針旋轉(zhuǎn)30°，函數(shù)就被擠壓成

師：不錯(cuò)，那大家是否能據(jù)此歸納出更一般性的結(jié)論呢？

經(jīng)過交流討論，學(xué)生得出了如下的定理.

定理：在平面直角坐標(biāo)系xOy中，保持y軸不動(dòng)，將x軸按逆時(shí)針旋轉(zhuǎn)α（0°＜α＜90°），則跟著被擠壓（或拉伸）后的函數(shù)k≠0）的圖像就是原坐標(biāo)系xOy中的函+tanα·x（k≠0，0°＜α＜90°）的圖像；將x軸順時(shí)針旋轉(zhuǎn)α，則擠壓（或拉伸）后的函數(shù)的圖像就是原坐標(biāo)系xOy中的函數(shù)-tanα·x（k≠0，0°＜α＜90°）的圖像.

（三）宜將剩勇追窮寇——繼續(xù)探究，擴(kuò)大戰(zhàn)果

經(jīng)過進(jìn)一步探究，學(xué)生發(fā)現(xiàn)，這不僅只是對(duì)反比例函數(shù)擠壓（或拉伸）才有效，對(duì)任意的冪函數(shù)y=xn，如果將x軸進(jìn)行旋轉(zhuǎn)，都有類似的結(jié)論成立.

推論1：在平面直角坐標(biāo)系xOy中，保持y軸不動(dòng)，將x軸逆時(shí)針旋轉(zhuǎn)α（0°＜α＜90°），則跟著被擠壓（或拉伸）后的函數(shù)y=kxn（k∈R，n∈R）的圖像就是原坐標(biāo)系xOy中的函數(shù)y=kxn+tanα·x（k∈R，n∈R，0°＜α＜90°）的圖像；將x軸順時(shí)針旋轉(zhuǎn)α（0°＜α＜90°），則擠壓（或拉伸）后的函數(shù)y=kxn（k∈R，n∈R）的圖像就是原坐標(biāo)系xOy中的函數(shù)y=kxn-tanα·x（k∈R，n∈R，0°＜α＜90°）的圖像.

比如，在平面直角坐標(biāo)系xOy中，將x軸逆時(shí)針旋轉(zhuǎn)45°，則函數(shù)y=x2的圖像也跟著變形，得到了函數(shù)y=x2+x的圖像，如圖8所示.

其實(shí)，對(duì)任意的函數(shù)f（x），也有這樣的結(jié)論，見推論2.

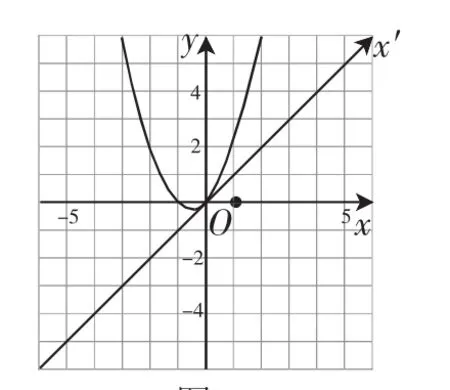
圖8

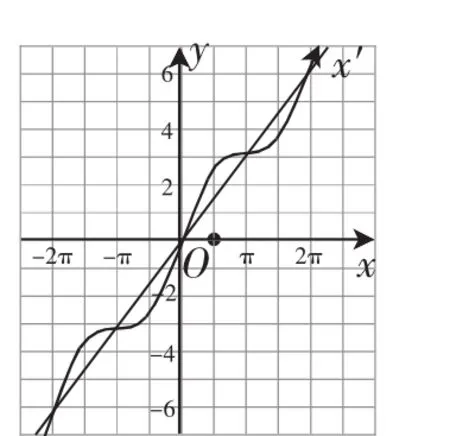
圖9

推論2：在平面直角坐標(biāo)系xOy中，保持y軸不動(dòng)，將x軸逆時(shí)針旋轉(zhuǎn)α（0°＜α＜90°），則跟著被擠壓（或拉伸）后的函數(shù)y=f（x）的圖像就是原坐標(biāo)系xOy中的函數(shù)y=f（x）+tanα·x（0°＜α＜90°）的圖像；將x軸順時(shí)針旋轉(zhuǎn)α（0°＜α＜90°），則擠壓（或拉伸）后的函數(shù)y=f（x）的圖像就是原坐標(biāo)系xOy中的函數(shù)y=f（x）-tanα·x（0°＜α＜90°）的圖像.

比如，在平面直角坐標(biāo)系xOy中，畫出函數(shù)y=sin x的圖像，現(xiàn)將x軸逆時(shí)針旋轉(zhuǎn)45°，則原函數(shù)y=sin x的圖像也跟著變形，得到了函數(shù)y=sin x+x的圖像，如圖9所示.

（四）吹盡狂沙始到金——深入思考，發(fā)現(xiàn)本質(zhì)

師：保持y軸不動(dòng)，對(duì)x軸旋轉(zhuǎn)角度α（0°＜α＜90°），其實(shí)質(zhì)是將原坐標(biāo)平面內(nèi)的每一個(gè)點(diǎn)（x，y）進(jìn)行了怎樣的變換呢？

生：其實(shí)就是把點(diǎn)（x，y）變成了點(diǎn)（x，y+tanα·x）.

師：同學(xué)們，那我們能否據(jù)此給坐標(biāo)軸的旋轉(zhuǎn)下一個(gè)定義呢？

經(jīng)過提煉與修正，學(xué)生最終得出了如下的定義.

坐標(biāo)軸旋轉(zhuǎn)：在平面直角坐標(biāo)系中，保持y軸不動(dòng)，對(duì)x軸旋轉(zhuǎn)角度α（-90°＜α＜90°），等價(jià)于將坐標(biāo)平面內(nèi)的任意一個(gè)點(diǎn)P（x，y）對(duì)應(yīng)成新的點(diǎn)P′（x，y+tanα·x）.

根據(jù)此定義，我們就不難理解剛才得到的定理與推論了.

此時(shí)課堂已近尾聲，但學(xué)生的探究熱情未減，于是筆者干脆讓同學(xué)們?cè)谡n后繼續(xù)分組研究，下面是其中一個(gè)小組極具創(chuàng)意的成果.

（五）喜看稻菽千重浪——課后研究，再結(jié)碩果

A小組的研究成果：

我們把情況從二維跨越到三維，想象現(xiàn)在眼前有一個(gè)空間直角坐標(biāo)系，其中O為原點(diǎn)，x軸，y軸，z軸兩兩垂直，那么空間中的每一個(gè)點(diǎn)都能被準(zhǔn)確定位.在日常生活中，這已滿足我們的需要.但在不同的環(huán)境下，一些超強(qiáng)的引力興許會(huì)扭曲這個(gè)時(shí)空，地球也不例外.

比如，在地球中，物體都會(huì)受到地球的萬有引力的影響.

如圖10，這是一座鐘塔，一開始，兩個(gè)鐘被調(diào)到相同的時(shí)間.但過了幾十年、幾百年，會(huì)發(fā)現(xiàn)上面的時(shí)間與下面所顯示的相差了幾秒.鐘當(dāng)然沒有問題，問題出在兩個(gè)鐘所在的時(shí)空受地球引力的影響而發(fā)生了扭曲，從而導(dǎo)致經(jīng)過的時(shí)間存在了差異.

若在某三維空間附近存在一強(qiáng)引力（比如，較大的恒星或黑洞），那么此三維空間便不再正常，即時(shí)空會(huì)出現(xiàn)扭曲.現(xiàn)以O(shè)為原點(diǎn)建立空間直角坐標(biāo)系，則空間的扭曲可看作是將某個(gè)（或某幾個(gè)）坐標(biāo)軸進(jìn)行了旋轉(zhuǎn)，于是我們可以用到之前得出的結(jié)論，即變化量分別為tanα·x或tanα·y或tanα·z.此時(shí)，若要求在強(qiáng)引力附近某物體的運(yùn)動(dòng)軌跡，我們就可以用坐標(biāo)軸旋轉(zhuǎn)的定義來解決.

圖10

舉個(gè)例子，假設(shè)某物體初始時(shí)是呈直線運(yùn)動(dòng)的，為了簡單起見，我們假設(shè)其運(yùn)動(dòng)軌跡為直線y=x，在經(jīng)過強(qiáng)引力附近時(shí)，若x軸發(fā)生了扭曲，設(shè)扭曲角為α（-90°＜α＜90°），則我們就可以計(jì)算出物體的實(shí)際運(yùn)動(dòng)軌跡為y=x+tanα·x.

二、教學(xué)感悟

本堂課筆者本希望能與學(xué)生共同研究函數(shù)y=（ab≠0）的圖像與性質(zhì)，卻止步于畫圖環(huán)節(jié)，真可謂是意外.但失之東隅卻收之桑榆，本課雖然沒有完成預(yù)設(shè)的教學(xué)任務(wù)，卻更好地培養(yǎng)了學(xué)生的數(shù)學(xué)核心素養(yǎng)，而且站在整個(gè)高中教學(xué)的視野下看，這樣的課堂意外，少了刻意的雕琢，多了靈氣的原生態(tài)，反而對(duì)學(xué)生的學(xué)習(xí)品質(zhì)的養(yǎng)成更為有利.

（一）順?biāo)浦郏嘤龑W(xué)生的直觀想象能力

直觀想象是指借助幾何直觀和空間想象感知事物的形態(tài)與變化，利用圖形理解和解決數(shù)學(xué)問題的過程.它主要包括：借助空間認(rèn)識(shí)事物的位置關(guān)系、形態(tài)變化與運(yùn)動(dòng)規(guī)律；利用圖形描述、分析數(shù)學(xué)問題；建立形與數(shù)的聯(lián)系等.

在本課中，教師原本預(yù)設(shè)了用描點(diǎn)作圖的方法來得到函的圖像，但學(xué)生卻意外地提出了旋轉(zhuǎn)法，此處的課堂生成是非常有價(jià)值的.我們知道，描點(diǎn)法雖然可以做到精細(xì)化作圖，但缺少了圖像動(dòng)態(tài)變化的過程，失去了培育學(xué)生直觀想象力的大好機(jī)會(huì).空間想象可分為靜態(tài)圖形的想象和動(dòng)態(tài)圖形的想象，其中動(dòng)態(tài)圖形的想象更為復(fù)雜，對(duì)思維要求更高，學(xué)生舍棄了相對(duì)“靜態(tài)”的描點(diǎn)法，采用了更為“動(dòng)態(tài)”的旋轉(zhuǎn)法，不失為一種上乘的選擇.同時(shí)，教師在課堂中順?biāo)浦郏瑺I造民主的學(xué)習(xí)氛圍，讓學(xué)生放開手腳大膽探索，讓學(xué)生的想象力得以自由釋放，從而探究出林林總總旋轉(zhuǎn)后的圖形，極大地培育了學(xué)生的直觀想象能力.

（二）適時(shí)引導(dǎo)，提升學(xué)生的數(shù)學(xué)抽象能力

數(shù)學(xué)抽象是指舍去事物的一切物理屬性，得到數(shù)學(xué)研究對(duì)象的思維過程.它主要包括：從數(shù)量與數(shù)量關(guān)系、圖形與圖形關(guān)系中抽象出數(shù)學(xué)概念及概念之間的關(guān)系，從事物的具體背景中抽象出一般規(guī)律和結(jié)構(gòu)，并且用數(shù)學(xué)符號(hào)或者數(shù)學(xué)術(shù)語予以表征.

在本課中，教師不斷改變函數(shù)的解析式，并適時(shí)引導(dǎo)學(xué)生從一個(gè)個(gè)具體的函數(shù)中抽象出最本質(zhì)的屬性，最終發(fā)現(xiàn)了圖形的旋轉(zhuǎn)與函數(shù)解析式之間的內(nèi)在關(guān)聯(lián)，從而得到了一般性的結(jié)論.這個(gè)過程就是數(shù)學(xué)抽象的過程，在這個(gè)抽象過程中，既有對(duì)圖形的抽象提煉，也有對(duì)代數(shù)解析式的抽象提煉，更有圖形和代數(shù)解析式之間關(guān)聯(lián)性的抽象提煉，可謂是把抽象思維的培育做到了淋漓盡致.

比如，從旋轉(zhuǎn)45°，到旋轉(zhuǎn)30°，再到旋轉(zhuǎn)α，這些是對(duì)圖形特征進(jìn)行抽象提煉；而從具體的反比例函數(shù)到一般的反比例函數(shù)再到函數(shù)y=kxn，最后推廣到函數(shù)y=（f x），則是對(duì)代數(shù)解析式的抽象提煉；至于將x軸逆時(shí)針旋轉(zhuǎn)45°，對(duì)應(yīng)著函數(shù)解析式值增加了x，從而抽象出將x軸逆時(shí)針旋轉(zhuǎn)α，對(duì)應(yīng)著函數(shù)解析式增加了tanα·x，則是對(duì)圖形和代數(shù)解析式之間關(guān)聯(lián)性的抽象提煉，而坐標(biāo)軸旋轉(zhuǎn)定義的形成更是將這種形與數(shù)之間關(guān)聯(lián)性的提煉推向了高潮.

（三）搭建平臺(tái)，發(fā)展學(xué)生的數(shù)學(xué)建模能力

數(shù)學(xué)建模是指對(duì)現(xiàn)實(shí)問題進(jìn)行數(shù)學(xué)抽象，用數(shù)學(xué)語言表達(dá)問題、用數(shù)學(xué)知識(shí)與方法構(gòu)建模型解決問題的過程.它主要包括：在實(shí)際情境中從數(shù)學(xué)的視角發(fā)現(xiàn)問題、提出問題、分析問題、構(gòu)建模型、求解結(jié)論、驗(yàn)證結(jié)果并改進(jìn)模型，最終解決實(shí)際問題.

由于課堂時(shí)間有限，教師鼓勵(lì)學(xué)生在課后繼續(xù)進(jìn)行分組探究，教師搭建了平臺(tái)，學(xué)生則登臺(tái)唱戲.每個(gè)研究小組都獲得了各自的研究成果，以A小組的研究成果為例，學(xué)生從實(shí)際問題出發(fā)，將課堂中二維坐標(biāo)系的旋轉(zhuǎn)升級(jí)為了三維空間坐標(biāo)系的旋轉(zhuǎn)，并給出了扭曲的時(shí)空中運(yùn)動(dòng)物體的定位方法，雖然觀點(diǎn)略顯稚嫩和粗糙，但難能可貴的是，學(xué)生已經(jīng)學(xué)會(huì)了運(yùn)用數(shù)學(xué)的眼光來看待實(shí)際問題，用數(shù)學(xué)的方法來分析實(shí)際問題，用數(shù)學(xué)的模型來刻畫實(shí)際問題.學(xué)生的數(shù)學(xué)建模能力在合作研究中得以發(fā)展，學(xué)生的數(shù)學(xué)視野也在交流碰撞中得以開闊.

1.水菊芳.基于數(shù)學(xué)核心素養(yǎng)的課堂數(shù)學(xué)意識(shí)的構(gòu)建［J］.數(shù)學(xué)通報(bào)，2016（11）.

2.任偉芳.為培育核心素養(yǎng)，凸顯概念教學(xué)過程而設(shè)計(jì)［J］.中學(xué)數(shù)學(xué)教學(xué)參考，2016（11）.

3.毛浙東.把握動(dòng)態(tài)生成，構(gòu)建和諧課堂［J］.中學(xué)數(shù)學(xué)教學(xué)參考，2008（9）.

4.毛浙東.數(shù)學(xué)概念課我們?nèi)绾紊系镁剩跩］.中學(xué)數(shù)學(xué)，2010（6）.F