數學教學：為理解而教，為理解而學
——“懂而不會”“會而不對”的成因分析及應對策略

☉四川省攀枝花市第十二中學校 張勇輝

一、問題提出

“懂、會、對”反映學生理解問題、解決問題的不同層次，由低到高呈遞進關系.“懂”是“會”的基礎，“真對”是“真懂”和“真會”的必然.在數學教學中，教師們總為一個普遍現象而苦惱，那就是學生“懂而不會”“會而不對”.這種現象到底是如何形成的？如何能有效地消減這種現象？許許多多的數學教師進行了大量的探究.筆者截取了日常教學的一些教學片段，選擇了高中數學學習中一些常見的例習題，來分析學生學習中“懂而不會”“會而不對”的成因，探尋教學應對策略.

二、“懂而不會”“會而不對”的成因分析

例1 已知向量a，b，c為非零向量，求證：a·b=a·c?a⊥（b-c）.（高中數學人教A版必修4第二章《平面向量》P108習題2.4B組第一題）

學生在做這個題的時候基本上沒有出錯，解題思路如下：a⊥（b-c）?a·（b-c）=0?a·b-a·c=0?a·b=a·c.解題思路清晰流暢，向量垂直的條件、向量的數量積的運算用得到位，可以說是行云流水，這讓我很放心，學生懂了！可是，一周后的一次檢測，有這樣一個填空題（選擇正確的選擇支），全班竟有的學生選擇了這個選擇支：已知向量a，b，c為非零向量，若a·b=a·c，則b=c.

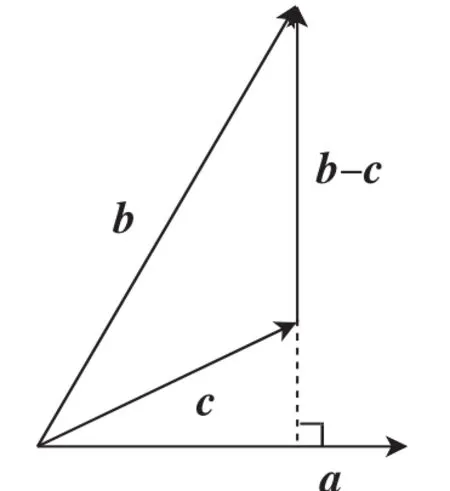
圖1

問題出在哪兒？怪學生沒有記住練過的那個習題的結論？顯然不能.我問了幾個出錯的同學，他們給出了一些理由：①沒細思考，當做實數運算處理了；②沒弄明白，覺得有點兒像是對的便選了！其實，他們并沒有真正弄懂a·b=a·c的含義：從數的方面看，a·b=a·c?|a||b|cosθ1=|a||c|cosθ2?|b|cosθ1=|c|cosθ2，從形的方面，則意味著向量b和c在向量a上的投影相等（如圖1，顯然a⊥（b-c））.

結語：從“懂”到“真懂”，需要思維的飛躍.學生所謂的“懂”，很多時候只是一種感覺，缺乏具體的衡量標準，懂得多與少、思維層次的深淺等等都是相對的.從本例來看，學生剛學完向量垂直的條件和向量的運算，在條件和結論間相互轉換并沒有太大的難度，但是，學生對a⊥（b-c）和a·b=a·c的意義及相關性（等價性）并沒有進行深入的探究，進而出現后面的解題錯誤.實際上，如果沒有教師的進一步引導，學生對這個問題的思考恐怕也很難深入.因此，教師在教學過程中的“導”非常重要，把學生從“懂”提升到“真懂”，就是一個把淺層思維導向深層思維的過程，進而達到真正理解的目標.否則，結果只可能是只“懂”不“會”！

例2 在△ABC中，b=

本題是學完正、余弦定理后的一個習題，學生1展示了她的解題思路：

①欲求a，應先求cos A（用余弦定理可求a），或求得sin A（用正弦定理可求a）；

②欲求cos A，sin A，先求sin C，cos C（利用cos A=-cos（B+C）=-cos B cos C+sin B sin C或sin A=sin（B+C））；

③sin C、cos C用正弦定理顯然可求，所以a可求.

實際上，在解題的思路上，她是正確的，對于余弦定理、正弦定理的運用有了一定程度的理解，可以說她是“會”了.細心地檢查，我們會發現，她在求sin C時出了錯，正確的是：si，計算能力的不足，導致最后解題失敗.假如，她沒在求sin C時出錯，后面的運算也完全正確的話，她是可以得出正確答案a=4或a=5.

但此處，我引著學生去反思，她選擇的方法是最好的嗎？結合已知條件，求a真的必須先求A嗎？有學生反應過來：選擇公式b2=c2+a2-2ca cos B，可以通過解關于a的一元二次方程，快速得到a=4或a=5.

反思兩種解法，反映出了對余弦定理在理解上的差異，第一種解法的思路被完全固定在了“求第三邊，必須知道另兩邊和所求邊的對角”，第二種解法則跳出了這個框框，轉換了思維角度，運用方程的思想靈活把握了余弦定理的本質“三邊與其中一邊所對角的關系”！思維品質上了一個臺階，選擇了更適合的方法，運算量因此銳減！

結語：從“會”到“真會”，還要學會對方法進行合理的選擇.選擇的解題方法不同，往往意味著解題過程的繁簡度不同，也直接反映出解題者效率的高低，但本質上卻反應出學生對一個問題的理解程度！我們可以清晰地看到：從“會”到“真會”尚有一段艱難的路要跋涉.

我不經意地問：“這下對了嗎？”“對了！”聲音非常整齊.我裝著準備寫下一個題，突然不放心似地轉身問：“真的對了嗎？”“當然！”聲音依然響亮！但我發現已經有同學不吱聲了，我決定不點破，知道有人會用行動回答我啦.

第二天課前，我提前來到班上，發現教室后黑板上已經有學生給出了正確的解答：

因為si舍去，此時A+B＞π），從而以下略去）

就是這樣一個常見的問題，經過了幾次反復，才最終“撥云見日”，難怪學生感嘆：要真正做對一個題太不容易！

結語：從“對”到“真對”，需要表達能力的提升，也需要對解題過程和結果進行重新審視.從“對”到“真對”，不僅要求學生要真懂，要學會選擇解題方法，還要求學生用批判的眼光審視解題的過程，去偽存真.“真對”，是有硬性的標準檢驗的，換句話說，“真對”，太不易.

教學是教與學的雙向過程，學生“懂而不會”“會而不對”，既有學生自身的原因，也有教師教學方面的原因，兩者如影隨形.

（一）學生方面的原因分析

第一，知識“斷面”.數學學習和任何其他學習一樣，都是一種認識的過程，而認識的過程都是通過自己已知的認知結構來加工新接觸的信息，也就是說從已有的知識結構中提取有效的舊知識以吸取新知識.這就需要找到新舊知識的連接點，即它們共通的地方，需要學生在頭腦中對新舊知識進行不斷分化和重新組合.但是由于每個學生的個人認知情況不同，有的學生在某一個問題的學習中如果不能順利實現新舊知識對接，就產生思維阻斷.一旦形成障礙，學生的思維“鏈條”斷裂，對新知識的學習只會停留于“表象”，所謂的“懂”也只是一種表象.

第二，思維“淺層”.根據英國的S.Pirie和加拿大的T.Kieren提出的數學理解動態模型分析，許多學生的數學學習只停留于模型的第一階段，即“初步了解”.比如，在例1的學習中，學生基本了解了兩向量垂直與向量數量積為0的關系，但淺嘗輒止，沒能從“形”的方向深入；基本了解了a·（b-c）=0?a·b-a·c=0?a·b=a·c的推斷，但沒有弄清這種轉換的意義，因而當同一個問題a·b=a·c在別的背景中出現時，形不成有效聯系.

第三，表達“障礙”.“說數學”是一種重要的數學能力，用口說，用筆“說”，都能很好培養學生的數學語言組織、邏輯思維和創新思維能力.然而在教學中，我們經常會發現不少學生不能闡述自己所學的知識，往往詞不達意、邏輯混亂，不能用規范的語言（文字、符號等）書寫.究其根源，還是因為學生對所學知識的來龍去脈沒有厘清，對所要解決的問題厘不清思路，找不到解決問題的途徑.

第四，方法“單一”.高中新課程新增了“三視圖”，是教學生多角度審視數學問題的好素材.由于學生對概念、定理、公式的運用條件和知識背景不熟悉，解題時很容易抓住一個貌似可以突破的地方入手，很難做到多角度觀察和思考，找到適合自己的最佳解題路徑，結果不是處處碰壁就是走了彎路.加之缺乏總結和反思，在同一問題上反復碰壁也將成為必然，“盲人摸象”的寓言在他們身上重復上演.

第五，審視“缺失”.很多學生沒有真正養成審視解題過程和結果的習慣，無法從定性分析和定量運算中發現解題中的錯誤.比如，有的學生解題中出現sin15°+，卻發現不了錯誤；再比如，例3中，C為△ABC的內角，學生3算出，卻沒有發現其中的錯誤.由于缺乏審視，學習過程中的錯誤被掩藏了.

我們不難發現，學生“懂而不會”“會而不對”的真正根源都在于對知識沒有真正的理解！

（二）教師教學方面的原因分析

從教師層面看，教學缺乏針對性是造成學生“懂而不會”“會而不對”的真正原因.由于實行師班教學制，數學教師的教學任務太重，一位教師上兩個班甚至三個班，面對一百多位學生，很容易出現以下兩個突出問題：一是對學生的學情分析不到位，不清楚學生學習的斷層所在.教學上趕進度、撒大網，備課針對性不強，不能對所出現的問題進行準確分析，更談不上準備充分的、針對性的材料彌補學生知識斷層.二是由于數學知識的理解需要在反復的思考和多次琢磨中才能完成，而一個班級學生的基礎、學習能力差異很大，有的學生理解一個問題可在很短的時間內完成，而有的學生則需要很長時間，教師很難準確判定學生對相關知識的理解程度.

即便是實施一些優秀的教學模式和方法，上述兩個方面的問題也不同程度地存在，需要下大力氣研究才能解決.比如，“先學后教”教學模式是對傳統的“先教后學、課后作業”教學模式的顛覆性改革，倡導學生自主學習、合作探究、交流展示，學生是學習的主體，教師在整個教學的過程中扮演組織者、指導者的角色，相對于傳統教學有其顯著的優點.在實施的過程中，我們會發現有一些問題仍然不易解決，如學生自主學習的成果展示的“話語權”容易掌握在“先行先知者”手中，當堂檢測的效果難以準確統計和評判，教師“零散”的點撥難以梳理知識的來龍去脈、構建完整的知識體系，提升思維水平等等.再比如，“變式訓練”作為優秀的數學教學傳統被長期堅持，但如果做不到促成學生思維“漸進式”生長，淺層次的“變式訓練”，只能是讓學生“依葫蘆畫瓢”，無法觸及問題的本質，引發深入思考，其結果是既浪費了時間，又無法真正將學生的思維引向深入，理解性學習成為空談.

三、關注理解性教學和學習是消減“懂而不會”“會而不對”的可行途徑

美國國家研究理事會在《人是如何學習的》報告中，總結了國際近30年從腦科學、神經科學、行為科學、心理學和教育學等多個學科角度對人類學習的研究成果，提出了學習科學的概念，其中有三條突出的基本學習原則：（1）原有的理解；（2）事實性知識和概念框架對理解的作用；（3）自我監控的重要性.在此研究基礎上，更進一步地提出了七個理解性學習的原則：（1）圍繞學科的主要概念和原理形成結構；（2）運用已有的知識建構新理解；（3）運用元認知促進學習；（4）學習者之間存在差異；（5）學習者的動機；（6）在實踐活動的情境中學習；（7）社會交互學習的共同體.這些原則同樣適合數學學習.新課程改革，倡導建構性的學習過程觀，把學習過程的重點從對事實的記憶轉向了對過程的理解.理解性學習關注學生的學習基礎，也關注過程的學習，重在獲得對學科核心概念和原理的深層理解，是一種有效的、有意義的學習.

“懂而不會”“會而不對”的真正癥結正是在于學生對知識和方法的理解程度不夠.因此，要消減這種現象，必須關注理解性學習，并把它切切實實落實在教學的每一個環節中.

首先，穩扎穩打練基礎.基本知識是解題的基礎，我們每一位教師都能認識到基礎知識的重要性，在教學過程中也都注重打基礎，但是，很多時候、很多地方我們做得不夠.一些值得推薦的做法有：（1）在學習新知識之前檢測學生學前知識的掌握程度，它是進一步理解的基礎，關系到學生對知識的建構；（2）堅持“日清”“周清”“月清”；（3）循環檢測學生基礎知識的掌握程度；（4）制訂過關的標準，精心編制基礎知識過關測試題，對學生進行逐級過關，界定學生基礎知識掌握的層次，為進一步夯實基礎提供有信度的依據.這項工作非常重要，不僅要求教師要掌握一定的測量理論，還必須具備非常扎實的專業功底，需要教師集體協作才有可能完成.

其次，活學活用練方法.基本知識和方法是分割不開的，前者是解題基礎，后者是解題的策略、手段和途徑，解題反過來又促進知識的內化、方法的活化.在學生掌握基礎知識的同時，強化對學生進行解題方法訓練.“一題多解”并不是說方法越多越好，最重要的是在學生理解掌握通性通法的基礎上，選擇最適合自己的、最佳的解法并固化下來，反復訓練，才能有效地遷移.以一場經典羽毛球賽為例，我們常常驚嘆球員精湛的球技，精準的擊發、到位的防守令人嘆為觀止.這一切精彩的表現無不來自于球員艱苦的訓練.發球、勾球、吊球、殺球，無不經過千萬次反復訓練，才能做到球到眼到、眼到心到、技由心生.數學學習也是如此.

第三，從從容容提能力.提能力是學生的期待，也是教師的責任，教師在提升能力方面起著非常重要的作用.需要強調的是，不能將打基礎、練方法同能力培養割裂開來，夯實基礎、熟練方法本身就能使學生獲得能力，也是學生進一步提高能力的基礎.學生能力的形成是“漸進式”的、“動態化”的，因此教師要把握好教學的進度和節奏，不能因為急于完成教學任務而加快學習進度，加大教學容量，超出學生理解的程度，而是要適時地為學生提供思考的機會，讓學生擁有思考空間去思考有能力思考的問題，不斷獲得更好的理解.同時學生理解力的提高還需要交流和表達，要讓學生積極參與交流，表達自己的觀點和認識，促進學生對理解的反思，在反思的過程中對自我認知進行辨別和調整，促進能力的自然形成和提高.所謂“從從容容”，就是要順其自然，拒絕拔苗助長！

理解是一種復雜的心理現象，理解性教學和理解性學習是一個復雜的過程.通過學生問題解決的表現去分析學生的理解程度，找出學生在理解上存在的困難，分析困難產生的原因，制定相應的輔助措施，才能真正促進學生對知識的理解，有效消減“懂而不會”“會而不對”現象.總之，懂、會、對——在理解中提升！

1.涂榮豹.數學建構主義學習的實質及其主要特征［J］.數學教育學報，1999（4）.

2.朱曼麗.基于理解的數學教學［J］.中學數學月刊，2012（2）.

3.羅新兵，石雪梅.數學理解性學習的條件分析［J］.中學數學教學參考，2012（12）.

4.胡青友.關注理解性學習［J］.教育科學論壇，2008（2）.H