一道解三角形測試題的命制與反思

☉四川省攀枝花市第三高級中學校 馮蓉波

2017年9月，我接到參加攀枝花市高三第一次統考數學試題命制工作的通知.筆者多次參加這種試題的命制工作，但以往主要任務是壓軸題.四川省從2017年起使用全國卷Ⅲ，風格發生了不小的變化.四川卷難易差距大，基本題簡單，壓軸題難；而全國卷不管大題小題中檔題居多，每題都有較大的思維容量.處在全國卷第17題的三角函數近幾年均考查與三角形相關問題，難度中等.對已經習慣多年第17題輕松得分的學生和老師來說這一題還有點不適應，加之從2017年開始，全國卷取消了選考題中的幾何證明選講，這意味著平面幾何的知識和方法將在其他題中體現.三角形正好是平面幾何知識與方法的良好載體，數形結合思想能得以充分體現，解三角形的試題在高考大題中的地位更加牢固.

一、靈感

三角形的五個“心”是三角形重要的幾何特征，湖南師大沈文選教授曾以三角形的五個“心”為載體，將競賽中的平面幾何問題作了歸類，使學生對平面幾何的學習更有條理.“重心”是高中生最熟悉的，它是三角形三邊中線的交點，一定在三角形內；“內心”是三角形內切圓的圓心，也是三角形內角平分線的交點，一定在三角形內.若能將三角形的重心與內心結合，圖形將豐富而生動，同時學生也不會感到陌生.

二、尋根

（一）三角形內角平分線相關結論

《人教版八年級上冊數學》第56頁拓廣探索12題［1］：

如圖1，在△ABC中，AD是它的角平分線. 求證：S△ABD∶S△ACD=AB∶AC.

（二）三角形中線長公式

《普通高中課程標準實驗教科書數學人教A版必修5》P20習題1.2A組13題［2］：△ABC三邊分別為a，b，c，邊BC，CA，AB上的中線分別記為ma，mb，mc，應用余弦定理證明：ma=

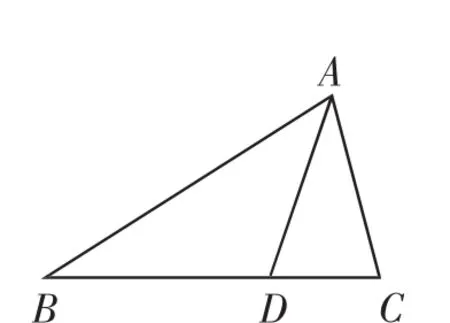
圖1

（三）2017年高考數學考試大綱

解三角形：（1）正弦定理、余弦定理：掌握正弦定理、余弦定理，并能解決一些簡單的三角形度量問題.（2）應用：能夠運用正弦定理、余弦定理等知識和方法解決一些與測量與幾何計算有關的實際問題［3］.

根據大綱要求，正弦定理、余弦定理的直接運用就是解三角形，即根據三角形三個獨立條件（已知三個角除外），求出三角形的其他元素，基本方法是用正弦定理、余弦定理（常常離不開三角形的內角和定理、面積公式等知識）［4］；基本方法就是邊角轉化，三個獨立條件往往不是直接給定，其中有的通過角的關系（三角方程）、邊的關系或邊角關系來給定，這時也考查了三角恒等變形的知識與方法.

（四）全國卷高考試題

（2015年全國卷Ⅱ第17題）在△ABC中，D是BC上的點，AD平分∠BAC，△ABD面積是△ADC面積的2倍.

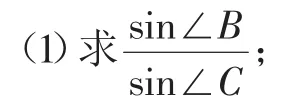
（2）若AD=1，求BD和AC的長.

運用課本基本知識與方法來編擬市統考題能追根溯源，運用高考原題的思路，既能體現這一章節的高考方向，又能考查這一部分基本方法與數學思想.

三、命制

（一）確定圖形

根據三角形全等的判定定理：SSS，SAS，ASA，AAS可確定唯一的三角形，而SSA（邊邊角）可能無解，或一解，或兩解（人教A版必修5P8-P9探究與發現有詳細討論）［2］.即根據三角形三個獨立條件（三個角除外），可以讓三角形定下來.由于是高三第一次統考，不能讓問題過于復雜，先確定一個等腰三角形：如圖2，a=c=2b=4，然后由點A出發作出中線與內角平分線.

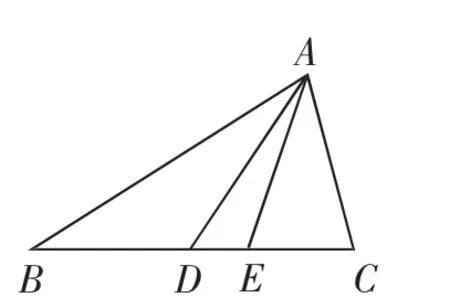
圖2

（二）設問

在圖2中，最引入注目的應是△ADE，從△ABC中不能得到任何一個直接的邊或角，所以一定要在△ADE上產生問題，第一感覺是“第（2）問：求△ADE的面積”.

第（1）問是求△ADE的邊長好還是求△ADE的內角的三角函數值呢？求△ADE的內角的三角函數值似乎這三條邊都要求，或利用差角或外角或補角來求，問題變得復雜.所以還是求△ADE某一邊或線段BE或CE的長好些.若求線段DE、BE或CE的長，第（2）問若求△ADE的面積可直接通過等高的三角形面積比等于底之比來求，變得很單薄.若求AE的長，學生可能會通過半角公式求出∠EAC的正弦或余弦，在△ACE中用正弦定理來解.而求AD的長直接與課本習題接軌簡單明了.于是決定將第（1）問設定為求線段AD的長.

第（2）問是求△ADE的面積還是求△ADE內切圓半徑（面積）或外接圓半徑（面積），求△ADE內切圓半徑（面積）不僅要求出△ADE的面積，還要求出△ADE的周，其中L為三角形的周長 ）；若求外接圓半徑（面積），則由正弦定理須求出某內角的正弦及對邊，主要是求角比較復雜.于是第（2）問設定為求△ADE的面積.

（三）推敲

△ABC的三個獨立條件用SSS給出會使問題顯得過于平淡，不便于考查三角恒等變換以及正余弦定理的應用.參考2017年全國卷Ⅲ第17題：△ABC的內角A，B，C的對邊分別為a，b，c，已知sin

（1）求c；

（2）設D為BC邊上一點，且AD⊥AC，求△ABD的面積.

△ABC的三個獨立條件用了邊邊角給出，只需用同角關系求出A角的正切值即可求出角A，比較輕松.模仿2017年全國卷Ⅲ，將“a=4”抹去，直接給出從方程的觀點來看這兩個方程在此三角形中是等價的，可以確定同一個三角形.

第1稿：如圖3，△ABC的內角A，B，C的對邊分別為a，b，c，D，E為線段BC上的點，AD，AE分別過△ABC的重心

與內心.已知c=2b=4，tan

（1）求線段AD的長；

（2）求△ADE的面積.

1.推敲1

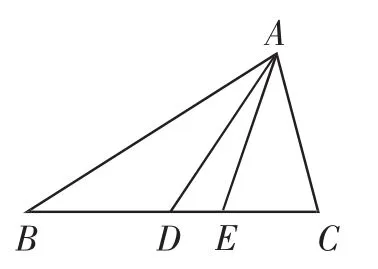
圖3

已知條件中強調了△ABC的重心與內心，概念性太強.如果學生不知道這兩個概念，此題將無法入手而得零分，這不是命題人的本意，所以要改變兩個條件的敘述.

第2稿：將第1稿中“AD，AE分別過△ABC的重心與內心”直接敘述為“BD=CD，∠BAE=∠CAE”.

2.推敲2

對比2017年全國卷Ⅲ第17題的難度，第（1）問相當，但全國卷Ⅲ的第（2）問變化多，如果不用面積比來實現求△ABD的面積，則須解△ABD，△ACD，但這兩個三角形都差一個條件，需建立方程來求解就難了.于該題的第（2）問變化并不多，可直接求底和高，常用思路并不困難，于是對tan的條件進行改變.變為“2c cos C=b”.

3.推敲3

方程2c cos C=b中如果學生發現b，c邊的關系，可直接求出cos，比第2稿更簡潔.但這里考查了學生

第3稿：將第1稿中的的觀察能力，能觀察得到這一結論獲得這一結果是對這類學生的獎償.若不能觀察出，則可用正弦定理進行邊化角，可得sin2C=sin B，因為b＜c，所以B＜C，所以B＜2C.

因為B，2C∈（0，2π），所以B+2C=π.

因為A+B+C=π，所以A=C.

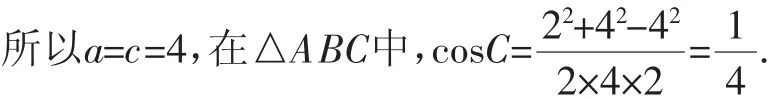
也可用余弦定理化為（c2+acb2>）=0.

而c2+ac-b2=12+4a＞0，所以a=c.所以a=c=4，

在△ABC中，也可得出cos

第4稿：將第3稿中的方程“2c cos C=b”變成與兩個角相關的等價條件“sin2C=sin B”.

4.推敲4

將方程“2c cos C=b”變成等價條件“sin2C=sin B”.學生由正弦定理變成“2c cos C=b”，進而得到cos得非常巧妙！這條路不明朗，可能性小.而用第3稿的方法直接用函數值相等得到角的方程可能性大.

這兩個條件的取舍上中心組成員也產生了很大的爭執，關鍵是直接給出兩邊是正弦值相等，方向誘導性很強，沒有邊角均有的“2c cos C=b”豐富.也設法變換成但小題中也出現誘導公式，這種變換也只增加了誘導公式的考查，沒有太大改變.權衡之下，最終還是選擇了第3稿.

（四）定稿

如圖4，△ABC的內角A，B，C的對邊分別為a，b，c，已知c=2b=4，2c cos C=b，D，E為線段BC上的點，且BD=CD，∠BAE=∠CAE.

（1）求線段AD的長；

（2）求△ADE的面積.

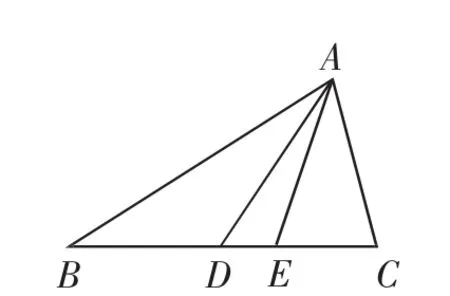
圖4

四、解答

（一）第（1）問分兩步

第1步：求a.

方法1：因為2c cos C=b

由余弦定理知，c2=a2+b2-2ab cos C?42=a2+22-2×2×a×

方法3：因為2c cos C=b，所以(c2+ac-b2=12+4a＞0，所以a=c.所以a=c=4.

第2步：求AD的長.

方法1（用中線長公式）：由a=4，得BD=2.

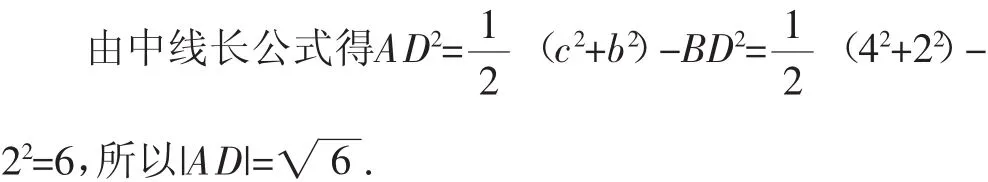
方法2（用余弦定理）：由a=4，得CD=2.

方法2：因為2c cos C=b，由正弦定理得sin2C=sin B.

因為b＜c，所以B＜C，所以B＜2C.

因為B，2C∈（0，2π），所以B+2C=π.

因為A+B+C=π，所以A=C.

所以a=c=4.

（二）第（2）問分兩步

第1步：求DE的長.

方法1（用正弦型面積公式）：因為

所以EC

方法2（用三角形內角平分線定理）：如圖5，過點E分別作AC，AB的垂線，垂足分別為F，G.

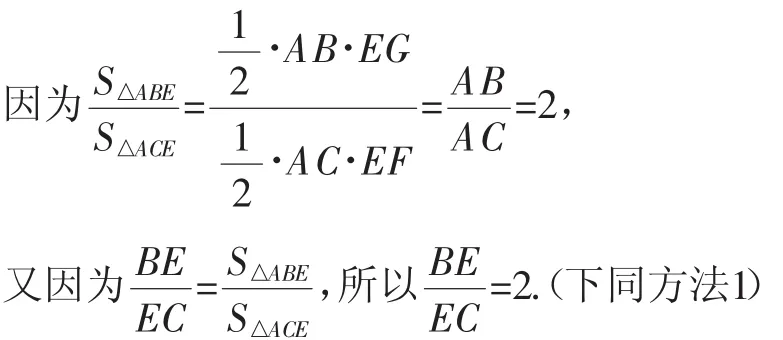
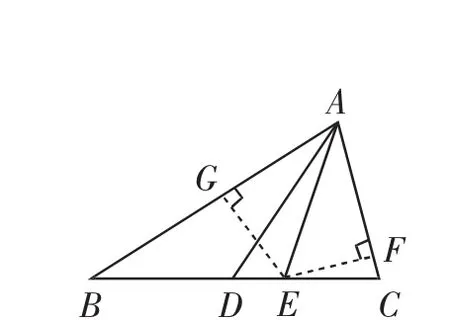
圖5

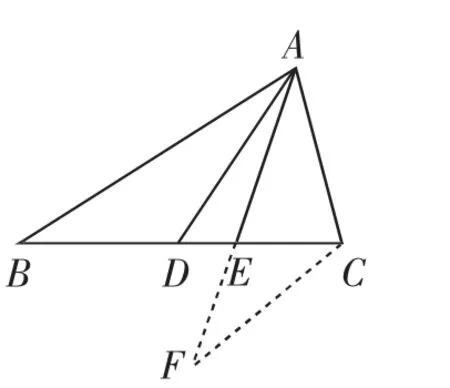
圖6

方法3（用相似形）：如圖6，過點C作AB的平行線交AE的延長線于F，則∠BAE=∠F，所以∠EAC=∠F，所以CF=AC.

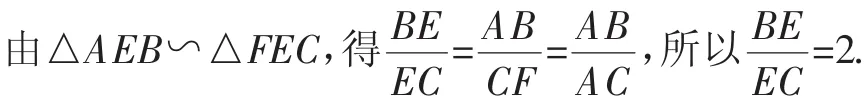
（下同方法1）

第2步：求△ADE的面積.

方法1（直接求高）：因為2c cos C=b，所以所以△ADE中，DE邊上的高為h=

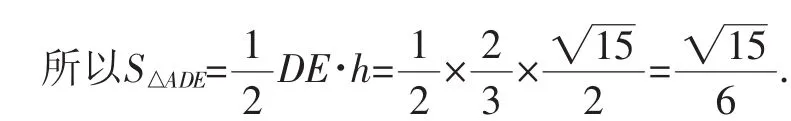
方法2（用等高的三角形面積比等于底之比）：因為2c cos C=b，所以cos

五、反思

（一）對兩道高考題與本題所用方法歸類

2017年全國卷Ⅲ第17題、2015年全國卷Ⅱ第17題以及本題的第（2）問都運用了同一方法：“等高的三角形的面積比等于底之比.”若推廣為含三角形式的結論為：

如圖7，在△ABC中，∠BAD=θ，∠CAD=φ.

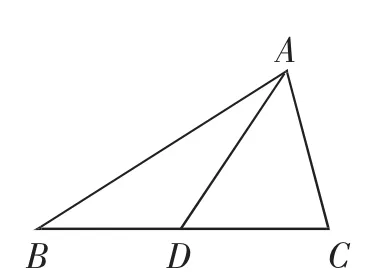
圖7

在2015年全國卷Ⅱ第17題以及本題中，θ=φ，所以

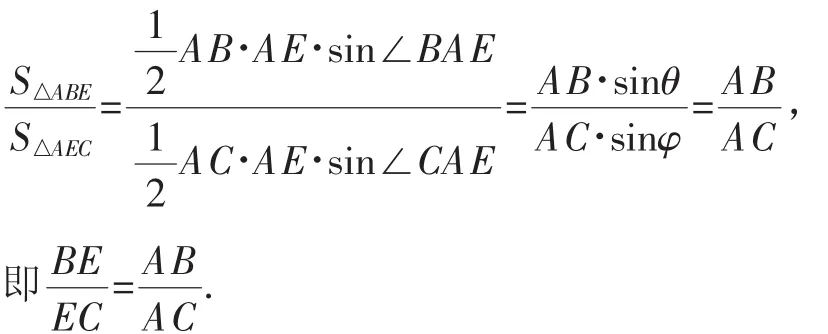
在2017年全國卷Ⅲ第17題中，θ=90°，φ=30°，

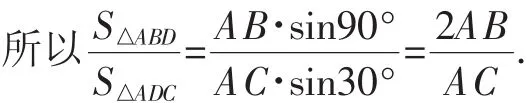
運用這個結論，所命制的統考題（定稿）還可以通過∠CAE來求∠DAE.

（二）對本題特點分析

本題緊扣教材與考綱，既考查學生的平面幾何的基本知識與方法，又考查了正弦定理余弦定理的應用與三角恒等變換的知識與方法，將三角形的面積比、邊長比、角的正弦值之比有機結合.難度適中，思維角度廣，解題方法多，也便于老師在考后運用本題對解三角形問題進行分析與歸納.

（三）對本題考試結果的反饋

本題全市理科平均分為6.2分，作為大題第一題，分數偏低.第（1）問大多數學生還能根據已知條件應用正余弦定理對△ABC和△ABD求解；在第（2）問很多學生試圖去求△ADE的內角來求面積而失敗，未能通過與△ABC的面積比來轉化.這是學生慣性，學生在題海中固化了這一方法.這說明了高三教師對近幾年高考題考查的方法與思路研究不夠，不能從提高學生關鍵能力的角度展開教學，還在題海之中.在第一次全市教研會上我引用了本題作了關于三角函數的微專題復習的發言.

（四）對試題命制的反思

作為命題小組成員，十多年來從模仿到改編，從改編到原創，歷經磨難，對自己總是難以滿意.究其原因：一是理論水平不高，二是素材積累不夠.因此，平時應反復理解數學核心素養的本質，多閱讀與試題命制相關的理論文章，也多學習同行的命題過程與心得，欣賞命題的內在本質與美，提升自身素養.多挖掘核心概念，對教材中的例題、習題等內容進行改編與整合，在課堂上學生提出的新的觀點、方法收集整理，在教研會上教師之間多交流碰撞，對高考試題鉆研、歸類，對競賽試題與高校自主招生試題多作研究，總會找到新的素材與方法，命制出滿意的試題.

1.人民教育出版社課程教材研究所中學數學課程教材研究開發中心.義務教育教科書八年級上冊數學［M］.北京：人民教育出版社，2013.

2.人民教育出版社課程教材研究所中學數學課程教材研究開發中心.普通高中課程標準實驗教科書數學必修5［M］.北京：人民教育出版社，2007.

3.教育部考試中心.2017年普通高等學校招生全國統一考試大綱理科［M］.北京：高等教育出版社，2016.

4.羅增儒.一道2017年高考三角試題的雙面剖析［J］.中學數學教學參考（上旬），2017（10）.H