護舷靠墊影響下的動力定位浮托安裝進船工況研究

劉天楓，王 磊，李 博，徐勝文

(1. 上海交通大學 海洋工程國家重點實驗室，上海 200240；2. 高新船舶與深海開發裝備協同創新中心（船海協創中心），上海 200240；3. 上海交通大學 船舶海洋與建筑工程學院，上海 200240)

0 引 言

根據國家海事組織（IMO）和各大船級社的定義，動力定位（DP）船舶是指利用推進器來將其位置和首向保持在固定的位置或預設的軌跡上的船舶[1]。一般來說，動力定位系統由位置測量、控制、推力三大系統組成，控制系統是動力定位系統的最核心組成部分[2]。

浮托安裝法適用于大型平臺的安裝作業，具有精準的對接能力和較大的載荷空間，在近年來被廣泛關注研究。Xia等[3]用數值模擬方法研究了小型平臺浮托安裝的運動響應，并在此基礎上進行了物理模型試驗。Hu[4]對浮托安裝過程中的非線性動力和環境載荷進行了研究。

進船過程是動力定位浮托安裝過程最重要的過程之一。進船過程中，為保護駁船和導管架結構，一般會在導管架樁腿上安裝護舷靠墊，護舷靠墊對動力定位駁船的影響很明顯，在研究動力定位系統中具有重要意義。對動力定位系統的研究自20世紀末以來引起了很多學者的重視。Balchen[5]最先提出了基于多元最優控制和卡爾曼濾波理論的控制方法。S?rensen[6]提出了針對小水線面海洋結構物的動力定位方法。Serraris[7]對1艘動力定位單體鉆井船進行了時域模擬研究，并與模型試驗結果進行對比。

本文通過建立時域模擬程序對考慮護舷靠墊影響的進船安裝過程進行數值模擬，并將結果與模型試驗結果進行比較，為動力定位浮托安裝系統設計和實地操作提供參考。

1 動力定位系統數學模型

1.1 波浪載荷

平臺的低頻運動是關注的焦點，在計算平臺低頻運動時，風力和流力均設為定常值，通過模型試驗結果決定，剩余需要重點關注的對象是2階波浪力。2階波浪力通常可以視為由低頻波浪力（差頻）、高頻波浪力（和頻）及平均漂移力組成，2階波浪力的幅值與入射波幅值的平方呈正比例關系。用2次傳遞函數（QTF）來表示只考慮低頻部分的二階波浪力[8]：

式中：為相位角；為波幅；為諧波的波浪頻率。一般的做法是通過商業軟件來計算二次傳遞函數，本文所用的二次傳遞函數由商業軟件HydroStar計算得出。

1.2 控制方法與推力系統分配策略

本文動力定位系統時域模擬程序的控制方法采用PID控制，控制方法如下式所示：

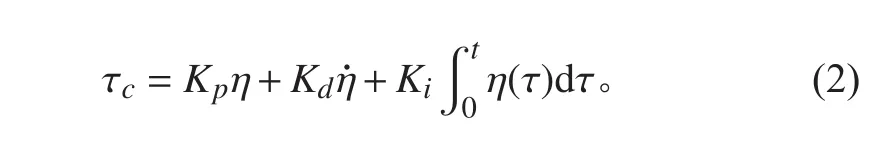
在推力系統中，控制系統所需要的推力將被分配到不同的推進器上，本文推力系統分配策略如式(3)所示，其解的最小值問題即代表推力分配策略的輸出結果[9]：

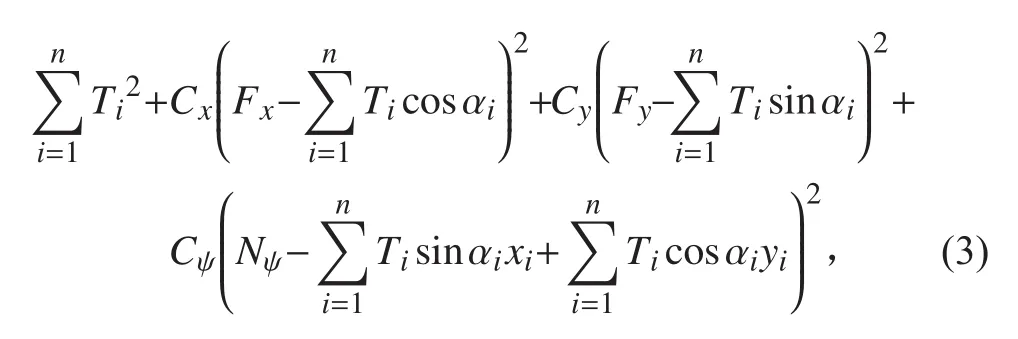
式中：Ti為第i個推進器輸出的力；n為推力器的數目；C為權重系數；αi為第i個推進器的方向；xi和yi分別為推進器相對于船舶重心的橫向和縱向位置。可以通過設置αi的取值范圍以考慮禁止角的問題，用意是避免推進器之間的干擾問題。分配策略得出各推進器的推力后，可通過下式計算推進器的功率：

式中：KQ為轉矩系數；KT為推力系數；D為螺旋槳的直徑。

2 數值模擬算例

2.1 模擬對象及環境參數

2.1.1 駁船尺度參數

本文的研究對象為裝備有動力定位系統的某駁船，該駁船將被用于某油田中心平臺上部模塊的運輸和浮托安裝作業。該駁船在進船工況下的主要參數如表1所示，駁船的總布置圖及型線圖如圖1所示。

2.1.2 導管架護舷靠墊

該駁船與導管架之間存在護舷靠墊，護舷靠墊被布置在導管架上，已知護舷靠墊的剛度曲線如圖2所示，橫軸表示護舷靠墊的壓縮變形量，縱軸左邊表示應力，縱軸右側表示壓縮能，壓縮變形量為72%時，護舷靠墊力達最大允許值。

表 1 進船工況駁船主尺度Tab. 1 Main dimension of barge during docking operation

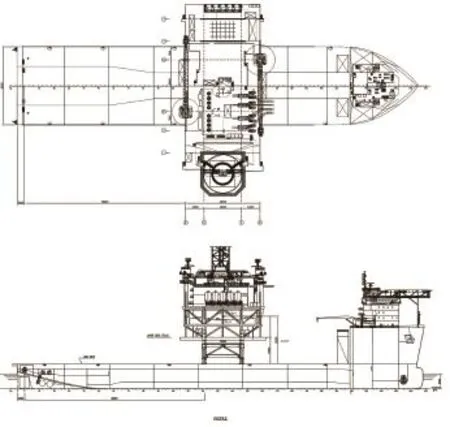
圖 1 某駁船總布置圖Fig. 1 General arrangement of the barge

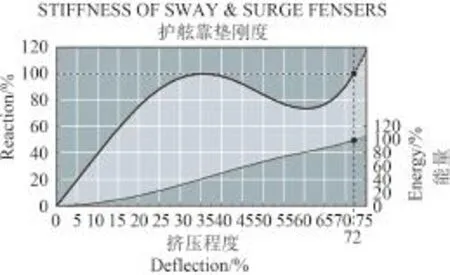
圖 2 護舷靠墊剛度Fig. 2 Stiffness of fenders

本文中，導管架上共有8只靠墊，其中橫向4只，縱向2只，護舷靠墊與駁船間隙值為0.1 m，位置布置如圖3所示，方框表示導管架的范圍，圓圈表示護舷靠墊所在位置，其中2/3/5/8號護舷靠墊位于上方，其下方對應護舷靠墊力為1/4/6/7號。

2.1.3 動力定位系統的推進器

圖 3 護舷靠墊位置布置Fig. 3 Position arrangement of fenders

本文研究對象駁船共配備7套推進器，其中2套主推進器、3套槽道推進器、2套全回轉推進器。各推進器的位置分布如圖4所示，主要性能以及具體位置參數如表2所示。

圖 4 推進器位置布置圖Fig. 4 Position arrangement of thrusters

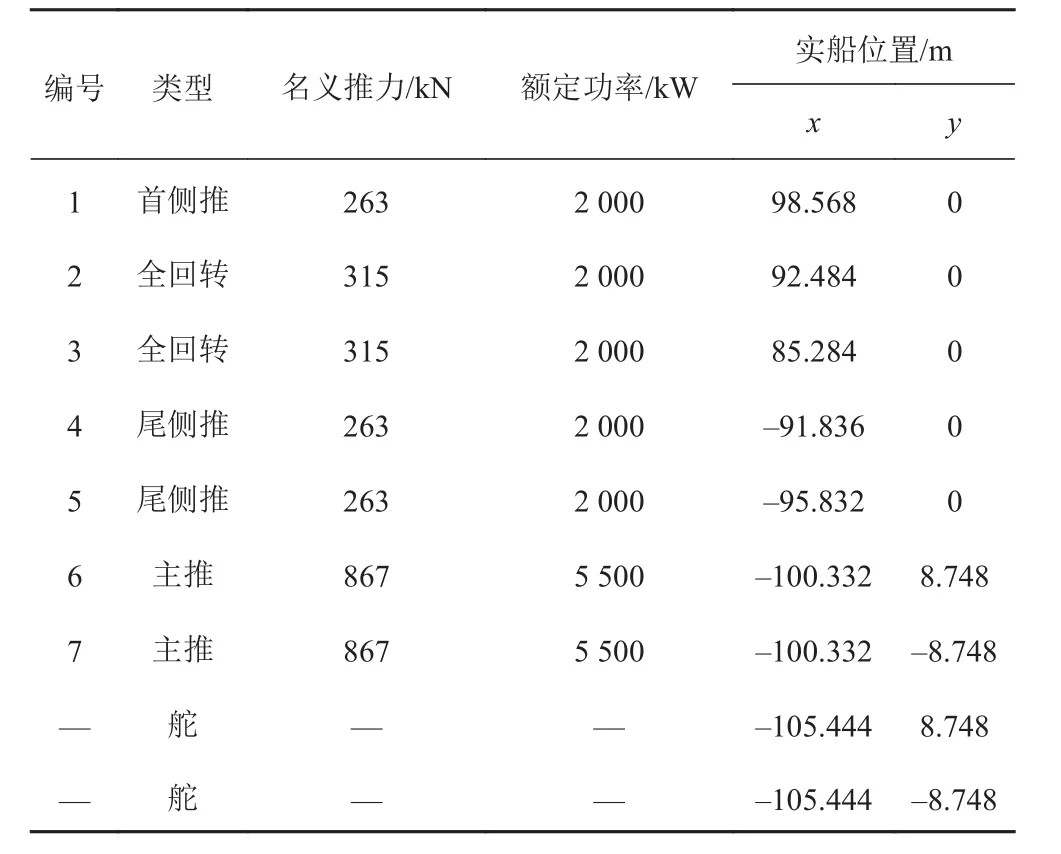
表 2 實船上的推進器各主要性能與相對重心處的水平位置Tab. 2 Main performances and horizontal positions of thrusters on real ship

2.1.4 海洋環境條件

本文時域模擬中的環境條件考慮了風力、波浪力、流力同時作用，波浪選用ISSC譜，風速和流速均采用定常值。本文模擬了90°/180°方向環境載荷下的浮托安裝進船過程，具體環境載荷參數如表3所示。

2.2 數值模擬方法

通過在Matlab/Simulink環境下編寫動力定位時域模擬程序，考慮護舷靠墊力對駁船影響，對動力定位浮托安裝進船過程進行數值模擬，時域模擬程序計算求解流程如圖5所示。

在時域模擬程序中，本文對護舷靠墊進行模擬。許鑫[10]在對浮托安裝系統耦合響應研究中提出一種計算護舷靠墊與駁船相互作用的方法，將駁船與護舷靠墊接觸的兩側看成一個接觸點與一個接觸面，通過點到面的距離來判斷靠墊作用力。本文考慮的工況中，將護舷靠墊簡化為4個位置固定的點，通過駁船的位置信息計算護舷靠墊與駁船舷側的距離，進而對護舷靠墊力進行計算。護舷靠墊力計算流程如圖6所示。本文中護舷靠墊與駁船舷側的間隔為0.1 m，護舷靠墊的厚度為1.2 m，最大壓縮值為0.864 m，此時壓力達到最大值328 t。

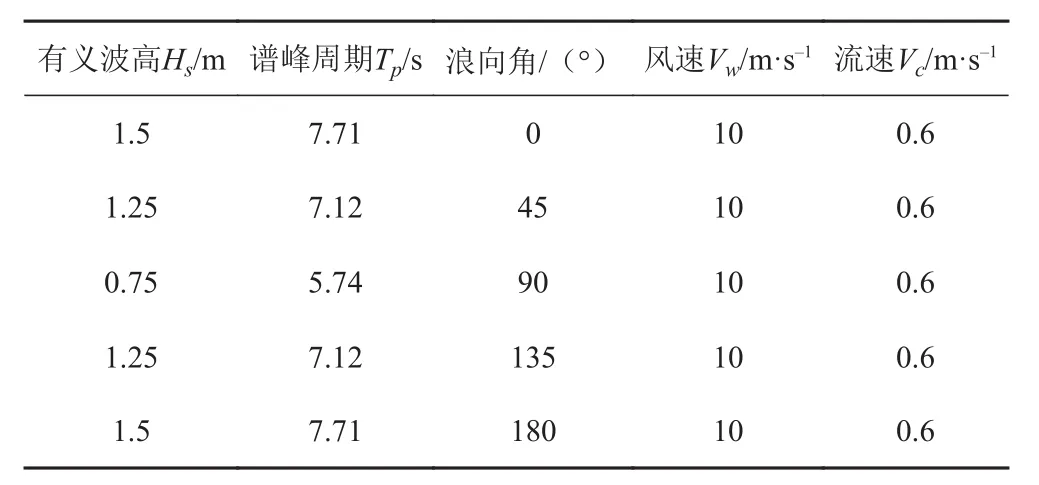
表 3 環境載荷參數Tab. 3 Parameters of environment conditions

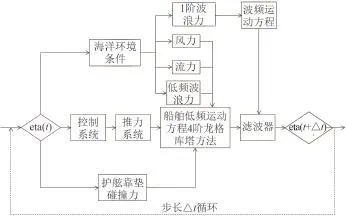
圖 5 時域模擬程序計算求解流程Fig. 5 Calculation process of time domain simulation program

2.3 數值模擬結果

2.3.1 90°浪向角模擬結果

90°浪向角下駁船橫向運動受外界影響較大，本文根據模擬結果得到其運動軌跡、首搖角以及護舷靠墊力如圖7～圖9所示，原點為定位目標點。

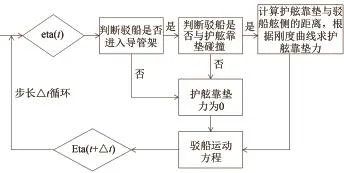
圖 6 護舷靠墊力計算流程Fig. 6 Calculation process of fender force

90°浪向角下，駁船受到橫向的環境力擾動較大，因此駁船的橫向位置偏移較大。模擬程序設定駁船與中心位置偏移量超過0.964 m時，護舷靠墊力將取最大值，在此情況下，駁船剛進入導管架中間時，偏離平衡位置較遠，故護舷靠墊力會呈現一段時間的最大值。

表 4 數值模擬護舷靠墊力統計Tab. 4 Simulation statistics of fender forces

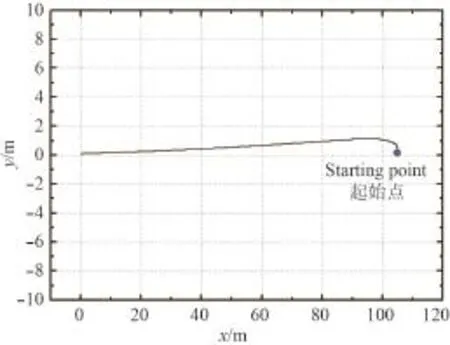
圖 7 90°浪向角駁船運動軌跡Fig. 7 Trail of barge movement (90° wave angle)

圖 8 90°浪向角駁船首搖角Fig. 8 Angle of yaw (90° wave angle)

圖 9 90°浪向角護舷靠墊力Fig. 9 Fender forces (90° wave angle)

2.3.2 180°浪向角模擬結果

本文給出180°浪向角下駁船運動軌跡、首搖角以及護舷靠墊力如圖10～圖12所示，原點為定位目標點。

180°浪向角工況下，環境力對駁船的橫向影響極小，因此除了系統剛啟動時的不穩定以外，其他時間段橫向偏移幾乎為0，護舷靠墊力也保持為0。

2.3.3 數值模擬結果分析

數值模擬結果中，90°浪向角工況下，fender1和fender3上的最大護舷靠墊力都達到了理論最大值328.33 t，fender2和fender4上則沒有護舷靠墊力出現，這一結果與90°工況下數值模擬的駁船軌跡結果相吻合；180°浪向角工況下，數值模擬結果顯示各護舷靠墊上的靠墊力為0，這是由于180°工況下駁船受到x方向的擾動較小，故沒有與護舷靠墊發生碰撞。

圖 10 180°浪向角駁船運動軌跡Fig. 10 Trail of barge movement (180° wave angle)

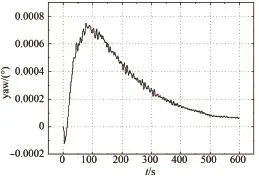
圖 11 180°浪向角駁船首搖角Fig. 11 Angle of yaw (180° wave angle)

圖 12 180°浪向角護舷靠墊力Fig. 12 Fender forces (180° wave angle)

3 模型試驗研究

3.1 試驗模型概述

模型試驗在上海交通大學海洋工程國家重點實驗室的風浪流水池中進行，為保證可比性，模型試驗對象與時域模擬對象為同一對象，縮尺比為λ=1∶36，實際水深為100.1 m，對應模型試驗水池水深為2.78 m。

駁船模型主尺度如表5所示，上部組塊主要參數如表6所示。

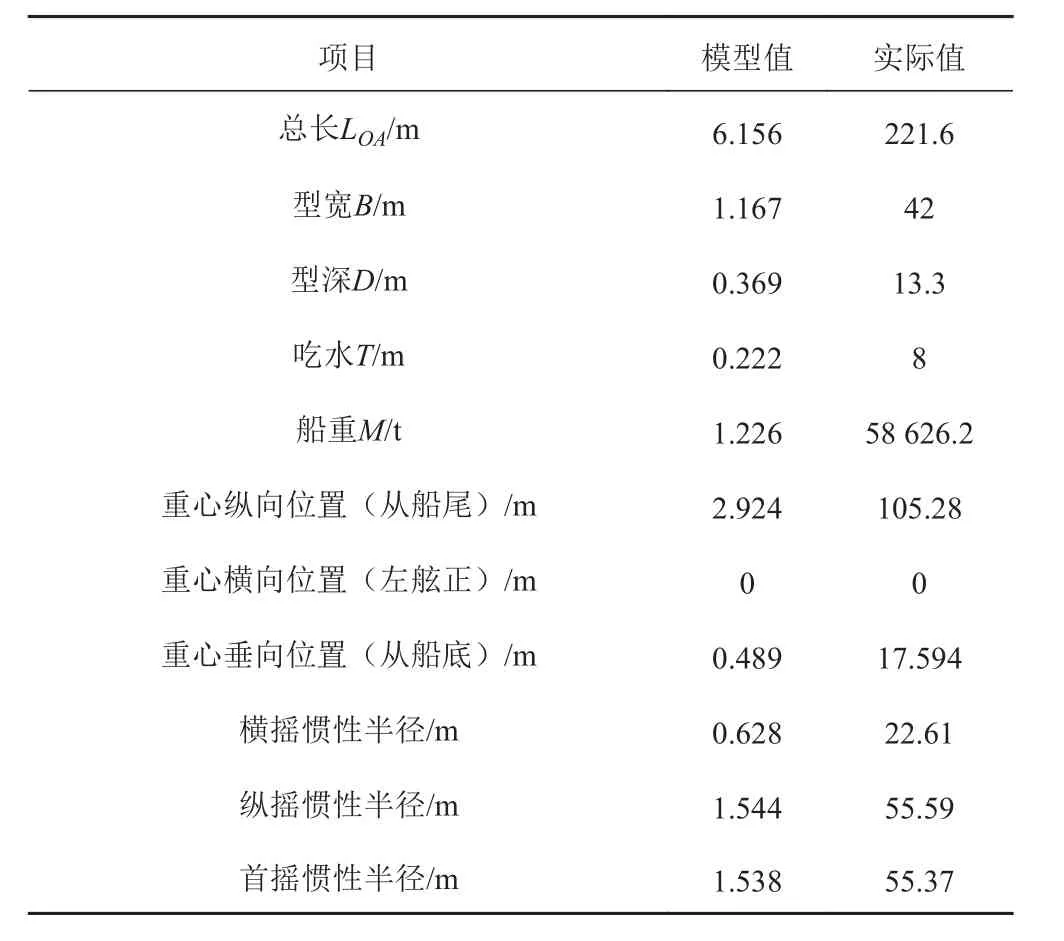
表 5 進船工況模型試驗駁船模型主尺度Tab. 5 Main dimension of model during docking operation

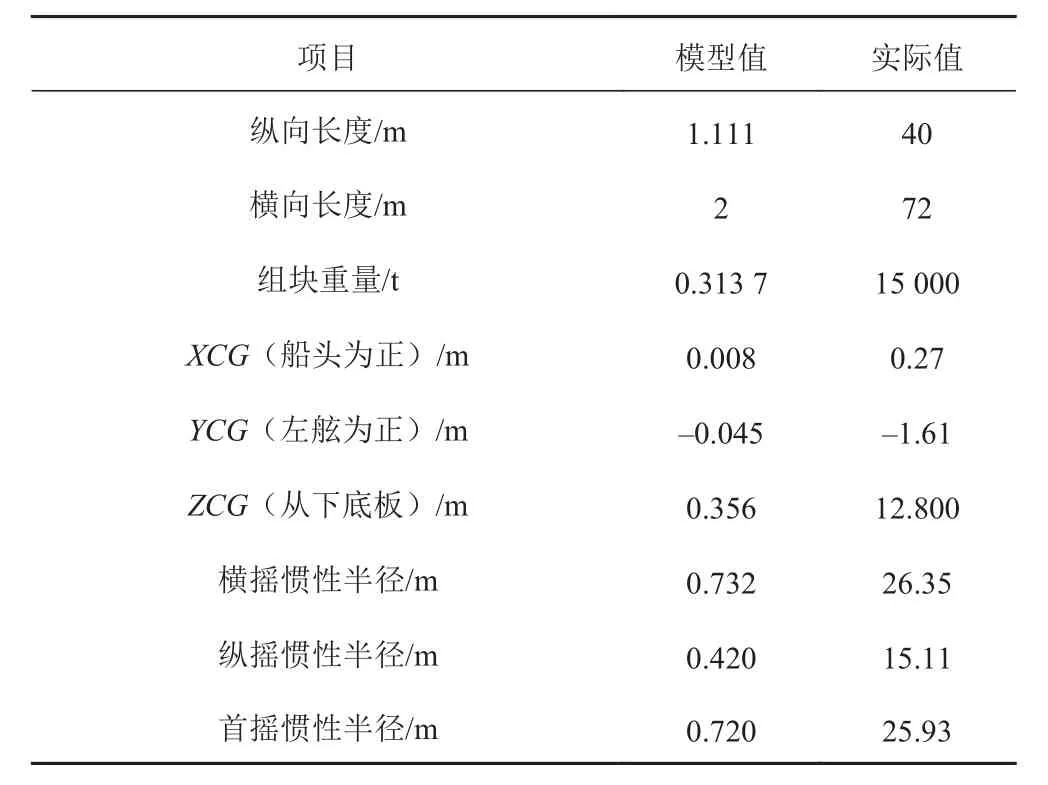
表 6 進船工況模型試驗上部組塊模型主要參數Tab. 6 Main dimension of upper block model during docking operation

3.2 海洋環境模擬

海洋環境的模擬主要包括對風、浪、流的模擬，模型試驗環境載荷參數如表7所示。對不規則波的模擬采用ISSC譜，根據有義波高、周期及波譜進行模擬，海洋工程國家重點實驗中中位于水池兩邊的造波機可以產生縱向和橫向的不規則波。圖13顯示了模型試驗中駁船在進船工況時的狀態。

表 7 模型試驗環境載荷參數Tab. 7 Environment condition parameter of model test

圖 13 模型試驗中進船工況試驗Fig. 13 Docking operation model test

3.3 試驗內容

試驗采用自主開發的動力定位控制系統，程序采用六自由度光學運動測量儀獲得駁船模型的實時運動信息，采用Kalman濾波估計海洋結構物的低頻運動，并由模糊PID控制器計算所需的環境補償力，總的推力和轉矩進而分配到各個推進器上。

本試驗共應用了5個不同的不規則波浪工況，試驗過程中所有的測量數據都被記錄在計算機中，以獲得足夠的數據進行統計分析。

3.4 模型試驗結果

經處理后，5種浪向角下動力定位駁船運動軌跡如圖14所示，定位目標點均為原點，駁船首向角如圖15所示。同時，試驗也采集了護舷靠墊力數據，統計結果如表8所示。

從靠墊壓力來看，180°和0°時進船過程較順利，對應的護舷靠墊力最大分別為158 t和185 t，在大多數時間里護舷靠墊壓力值小于100 t。135°，90°，45°時，在大多數時間里護舷靠墊壓力值大于 100 t，對應最大護舷靠墊壓力值分別為205 t，214 t和212 t。180°，0°，90°進船難度較低，135°和 45°進船較為困難。

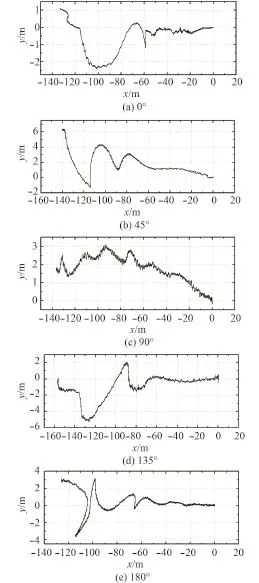
圖 14 模型試驗駁船運動軌跡Fig. 14 Model test trail of movements

4 結 語

本文對某應用動力定位技術的浮托安裝進船過程進行了數值模擬研究，在數值模擬的過程中考慮了護舷靠墊對進船過程中駁船的影響，得到了90°工況和180°工況下駁船的運動軌跡、首搖角時歷曲線、護舷靠墊力時歷曲線。此外，本文還討論了該動力定位浮托安裝進船過程的模型試驗研究，通過對比結合得到以下結論：

動力定位浮托安裝進船過程中，護舷靠墊對駁船有較明顯的影響，特別是在90°浪向角工況下，護舷靠墊力也是在此工況下達到最大值，實際工程中需注意相應海洋環境下護舷靠墊設計的安全冗余。

圖 15 模型試驗駁船首搖角Fig. 15 Model test angle of yaw

表 8 模型試驗護舷靠墊力最大值統計Tab. 8 Maximum fender forces of model test

從護舷靠墊力模擬結果上來看，數值模擬結果與模型試驗結果存在一定的差異。在數值模擬結果中，護舷靠墊力在180°浪向角工況下保持為0，而在模型試驗中，各個護舷靠墊都存在碰撞力，受撞擊的情況較為明顯；比較關系上，模型試驗中90°工況下的平均最大護舷靠墊力為139.5 t，顯著大于0°和180°工況下平均最大護舷靠墊力111.9 t和96.6 t，該結果與數值模擬結果相吻合。造成護舷靠墊力差異的原因可能有：1）模型試驗中對海洋環境的模擬無法做到完全理想化，導致結果的差異；2）數值模擬只考慮了水平面上的二維問題，與實際情況存在差異，導致模擬結果與實際情況可能存在差異。從軌跡上來看，數值模擬中90°工況y方向最大偏移量為1.13 m，平均偏移量為0.65 m，而模型試驗中，最大偏移量為3.10 m，平均偏移量為1.79 m，同樣在180°工況下，數值模擬中的最大和平均偏移量分別為 1.04×10–3m 和 3.8×10–4m，模型試驗中最大和平均偏移量分別為3.66 m和0.32 m，二者的結果在數量級上吻合，但在數值上存在一定差異。除了前文所述2條原因之外，動力定位系統剛剛啟動時系統尚未達到穩定狀態也是導致誤差的原因之一，會導致運動軌跡在定位初始階段存在較大的偏移。

從駁船運動軌跡上來看，考慮護舷靠墊影響的數值模擬研究與模型試驗研究結果具有一定的吻合，說明數值模擬研究對動力定位浮托安裝進船過程具有一定的指導意義，在未來動力定位系統設計過程中，可使用數值模擬研究作為輔助手段。

[1] S?RENSEN A J. A survey of dynamic positioning control systems [J]. Annual Reviews in Control, 2011, 35.

[2] 趙志高, 楊建民, 王磊, 等. 動力定位系統發展狀況及研究方法[J]. 海洋工程, 2002, 20 (1): 91-97.

[3] XIA J, HAYNE S, MACFARLANE G. Investigation into float-over installation of minimal platforms by hydrodynamic model testing [C]//Greece: Proceeding of OMAE2005 24th International Conference on Offshore Mechanics and Artic Engineering, 2005.

[4] HU Zhi-huan, et al. Nonlinear dynamics and impact load in float-over installation [J]. Applied Ocean Research, 2017, 65.

[5] J G BALCHEN, N A JENSSEN and S SAELID. Dynamic positioning using Kalman filtering and optimal control theory[C]//In IFAC/IFIP Symposium on Automation in Offshore Oil Field Operation, 1976.

[6] S?RENSEN A J, STRAND J P. Positioning of smallwaterplane-area marine constructions with roll and pitch damping [J]. Control Engineering Practice, 2000, 8.

[7] JORRIT-Jan SERRARIS. Time domain analysis for DP simulations [C]//Asme International Conference on Ocean,2009: 595-605.

[8] FALTINSEN O M. Sea loads on ships and offshore structures[M]. Cambridge: Cambridge university press, 1993.

[9] MARIN. Marin dpsim user guide [M]. MARIN.

[10] 許鑫. 浮托安裝系統耦合動力響應研究[D]. 上海: 上海交通大學, 2014.