聚焦“方程和不等式”應用型問題分析

江蘇省海門市能仁中學 花永平

在課程改革和課標理念的指導下，中考命題出現了能力立意和題型創新的新型試題，考試的基本核心不僅對基本知識和基本方法的考查，更加注重了對考生學習潛能的考查，并注重為初中數學學習全面提高，切實提升現代學生的核心素養，全面提高學生的應試能力。本文結合具體例子對方程與不等式，從其綜合生長的角度涵蓋三個方面：（1）用函數圖象求方程的解和不等式的解集。（2）用幾何融合探索方程的解和不等式的解集。（3）用流程圖涵蓋方程的解和不等式的解集。幫助大家將所學知識進行合理的串聯和有效的融合，從而對方程和不等式知識有一個再認識、再提升的過程

一、用函數圖象求方程的解和不等式的解集

用函數圖象來求方程的解和不等式的解集。重點是關注這條直線與x軸交點的橫坐標就是對應方程的解。而求不等式的解集就是看這條直線在x軸上方或者下方部分對應的橫坐標所構成的集合即為不等式的解集。

例1 在平面直角坐標系中，畫出的圖象，從圖象中可以發現哪些信息？

【分析】可以發現信息：

（1）直線和x軸、y軸的交點分別為A（-3，0）、B（0，4）；

（2）直線經過一、二、三象限，并且從左向右呈上升趨勢；

（3）△AOB的面積；

（4）的解，即為A點的橫坐標；

（5）當x﹥-3時，y﹥0；當x﹤-3時，y﹤0。

【點撥】以上信息都是從圖象中直觀得出來的，你發現了嗎？

你還能發現什么或提出什么問題？如：

（1）當x滿足什么條件時，y﹥2？（在圖中找出對應的直線在y=2的上方部分對應的x的范圍，即為不等的解集）

（2）方的解為正數，求k的取值范圍？（在圖中找出對應的直線與y=k的交點橫坐標大于0時，找k的取值范圍）

（3有兩解，且有一解大于-1，求k的取值范圍？

【點撥】對于以上問題，注重開放，考查探究能力和創新能力。每年的中考題會出現一些讓人耳目一新的題，他們的精巧的構思、生機盎然地呈現形式讓人注目。這些題常中見拙，拙中見巧，為不同程度的學生提供展示自己才華的平臺。假如從方程本身去思考，需分類討論；假如借助函數圖象，解題更直觀清晰。

二、用幾何融合探索方程的解和不等式的解集

例2 市區某中學九年級學生步行到郊外春游。一班的學生組成前隊，速度為4km/h，二班的學生組成后隊，速度為6 km/h。前隊出發1 h后，后隊才出發，同時，后隊派一名聯絡員騎自行車在兩隊之間不間斷地來回進行聯絡，他騎車的速度為12 km/h。若不計隊伍的長度，聯絡員在行進過程中，離前隊的路程y（km）與后隊行進時間x（h）之間存在著某種函數關系。

（1）求后隊追到前隊所用的時間的值；

（2）聯絡員從出發到他折返后第一次與后隊相遇的過程中，求此函數關系表達式，并在直角坐標系中畫出此函數的圖象；

（3）聯絡員從出發到他折返后第一次與后隊相遇的過程中，當x為何值時，他離前隊的路程與他離后隊的路程相等？

【分析】（1）當x=0時，一班組成的前隊出發1小時，二班組成的后隊準備出發，兩隊相差4 km，接著后隊和前隊進行追及問題，只要簡單構建方程就行了。

后隊追及前隊：4+4x=6x。

聯絡員追及前隊：4+4x=12x 解得x=0.5，故AC長度為6 km。

（2）當x=0.5時，聯絡員開始折返，他與后隊進行的是相遇運動，后前隊做的是背向運動。

聯絡員和后隊作相遇運動，他們的相遇時間：6x+12（x-0.5）=6，解

聯絡員和前隊作背向運動，他們的相距的距離：y=(4+12)(x-0.5) 。

（3）要看聯絡員在追上前隊前，還是在追上前隊返回過程中，他離前隊的路程與他離后隊的路程相等，我們可以利用直線圖，合理構造方程即可。

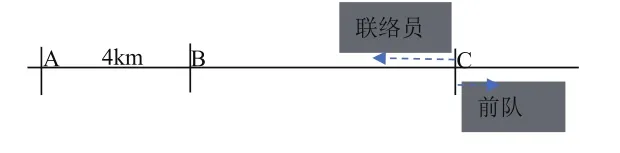
【點撥】針對上述問題，所涉及的數學量比較多，信息量比較大，運動關系比較復雜，對于這一類問題，指導學生經歷用觀察、畫圖、計算等手段，合理求解。

【思考】同學可以想一想：聯絡員從出發到他折返后第一次與后隊相遇的過程中，當x為何值時，他離前隊的路程大于他離后隊的路程（他離前隊的路程小于他離后隊的路程）？

【點撥】用函數的圖象來解決該問題也不失為一個很好的方法。

三、用流程圖涵蓋方程的解和不等式的解集

例3 對一個實數按如圖所示的流程圖進行操作，規定程序運行從“輸入一個實數x”至“判斷結果是否大于244”為一次操作。

（1）若輸入實數x=11，則輸出的結果是__________；

（2）輸出的結果可能會是352嗎？

（3）若操作恰好進行四次才停止，求x的取值范圍；

【分析】第一次：3x-2，第二次：3（3x-2）-2=9x-8，第三次：3（9x-8）-2=27x-26，第四次：3（27x-26）-2=81x-80，第五次：……

第二問：用方程思想去解答（需要分類討論）： 若是一次出結果3x-2=352，則x=118。若是兩次出結果9x-8=352，則x=40；若是三次出結果27x-26=352，則x=14；若是四次出結果81x-80=352，則x=5.333（舍去）。

第三問：建立不等式解答：27x-26≤244且 81x-80 ＞352，解得4＜x≤10。

【點撥】本題的流程圖，看似沒有方程和不等式，其實它考查的本質就是方程和不等式，而同學們在解題就是時要抓住問題的本質，追本溯源解決問題。

總之，我們教師應針對初中課數學課程改革和中考的命題，在學生備考試題時要有的放矢，注意關注中考信息，認真分析考點考什么，學生做什么，考到哪個層次，就把訓練的標準定到哪個層次，做到以課本為基礎，讓學生終身學習到生活中必須的數學知識和科學的數學方法，在學習過程中培養學生的能力，真正切實提高學生運用知識解決問題的能力。方程、不等式的試題多樣，形式多變，方法多用，而解決該類問題的關鍵是弄清問題中所涉及的數量關系，選取適當的方法，這樣離解決問題就近在咫尺了。這樣，學生在中考的舞臺上就能大展拳腳。