詮釋概念與要義，滲透思想與方法
——以蘇科版“數軸”的教學為例

☉江蘇省蘇州高新區實驗初級中學 丁 香

數軸作為數與圖像完美結合的橋梁，在數學研究領域有著重要的作用，新課標也對“數軸”內容提出了“還原數軸”“理解數軸”“滲透思想”的要求.對于數軸相關知識教學，也應基于上述要求，合理設置教學環節.以下以蘇科版七年級上冊“數軸”教材內容為例開展教學探討，提出教學建議.

一、基于已有經驗，詮釋數軸概念

數軸是初中數學深入學習與研究的工具，學生在小學階段已經初步接觸過數軸，對其有著較為粗淺的認識，數軸教學的開展可以在學生已有的知識經驗上進行.另外，由于數軸的概念較為抽象，但生活中存在數軸的原型，因此對于其概念的形成可以從生活實際中抽象，利用學生經常接觸的實物完成概念意義的教學.

數軸學習的初始階段需要激活學生的已有經驗，學生在小學階段學習過根據直線上點的位置寫出具體的數，即利用數來表示點，可以對該知識經驗進行合理拓展，使學生對數軸的三個基本觀念形成深刻的認識.引入如下活動：圖1直線上的點對應著不同的數，請根據點的位置在相應的方框里寫出具體的數.直線上的點是依次排列的，這樣的活動可以幫助學生認識直線上數的大小關系，而數與點的對應關系，以及直線的方向性對于學生后續理解“點”“直線”“數”極為有利.

圖1

圖2

數軸的概念抽象可以聯系生活中的直尺和溫度計，如圖2，利用兩者的刻度排列使學生理解數的實際意義，如讓學生思考刻度上的“0”所代表的含義，以及溫度計上如何表示“零上6℃”和“零下6℃”.在此基礎上通過類比讓學生思考能否繪出一條直線，用直線上的點表示正數、0和負數，從而引出后續的探究.學生對于繪圖一般有極大的興趣，概念教學可以設置繪圖活動，讓學生通過動手實踐的方式認識數軸的概念.活動如下：（1）首先畫一條水平的直線，在直線上取一點為0，定為原點；（2）要求直線向右為正方向，并用箭頭表示，向左為負方向；（3）在直線上取適當的單位長度，然后從原點向右每隔單位長度取一點，標為“1、2、3、4……”，原點向左同樣每隔一單位長度取一點，標為“－1、－2、－3、－4……”，如圖3所示.通過這樣的三個活動步驟，類比直尺和溫度計完成了數軸的繪制，然后引導學生理解這樣的具有原點、規定方向及單位長度的直線就是數軸，從而完成數軸的概念教學.

圖3

數軸概念教學中引導學生回顧已有知識經驗，喚起學生對于數與點對應關系的認識，結合生活經驗，類比生活實物，通過繪圖的方式使學生體驗數軸的繪制過程，從而理解數軸的概念和三要素.這樣的教學編排符合學生的認知規律，不僅完成了從經驗到知識的過渡，還在活動中鍛煉了學生的繪圖操作能力.

二、構建完整數系，深化“表示”要義

數軸上的點和數是相對應的關系，用點可以表示數，這是對數軸“表示”作用的充分體現.而對于數軸的深入教學需要依托數軸直觀的表示作用，實現數系在數軸上的完整構建，尤其是在數軸上采用合適的方式引入無理數，使學生深刻體會數軸的“表示”要義.

學生初步掌握數軸的概念后可以編排一定的練習，讓學生在數軸上標出數來體會數軸對數的表示作用，如給出下列各數：－3、、0、2.2、、4，要求學生在數軸上將其標出.同時給出如下要求：將點標在線的上方，數標在點的下方，然后讓學生觀察數軸思考問題：（1）通過數軸可以總結出點與數的什么關系？（2）上面的數都可以在數軸上表示出來嗎？哪些數可以在數軸上表示出來？通過追問思考，可以進一步使學生理解數軸的“表示”要義，即數與點的對應關系.另外，由于問題中給出的數包含了小數、分數、整數、負數和正數等不同類型的數，學生可以初步總結出關于數的表示規律：一是數軸上的點可以表示分數；二是數軸上的點可以表示有理數.對于有理數的表示，采用簡單的繪圖、思考、總結的教學方式，學生經歷了形象思維向理性思考的過渡，完成了數與點對應表示的初步學習.

數軸上的點除了可以表示有理數，還可以表示無理數，這是數軸完整性表示作用的體現，因此在教學中需要引導學生理解在數軸上也可以表示無理數，這是構建完整數系不可或缺的環節.可以讓學生思考：數軸上有許多表示有理數的點，但是這些點并不能將整個數軸布滿，那么數軸還可以表示哪些數呢？接下來可以編排如下兩個活動，從學生熟悉的問題中引入無理數：（1）面積為2的正方形，它的邊長a是無理數，如何在數軸上表示出來？（2）圓周率π是無限不循環的無理數，數軸上是否可以表示出來？如何操作？讓學生思考兩個無理數的表示方法，引導學生借助無理數對應線段來確定無理數在數軸上對應的點，如正方形邊長a的表示，先以數軸為對角線作面積為2的正方形，然后以原點為圓心、a為半徑畫弧，則弧與數軸的交點A就為無理數a，如圖4所示.無理數的數軸表示是一個相對復雜的過程，但是學習數軸“表示”要義的重要部分，借助直觀的畫圖來表示無理數，可以輔助學生理解.

圖4

數軸上有理數與無理數的對應表示是數軸“表示”要義的重要內容，也是構建完整數系的重要環節，對于學生理解數軸是連續點的結合是十分有利的.在無理數的表示中采用實驗作圖的方式，是對學生實驗思想的初步培養.另外，無理數形成的內在機理對于拓展學生的思維具有極大的幫助.

三、滲透數學思想，促進思想提升

對于“數軸”內容的教學，不應局限于基本的知識內容，還應該在教學環節、內容設置上滲透數學的思想方法，通過合理的教學編排實現學生思想和能力的全面提升.數軸的概念是對生活問題的抽象，可以滲透抽象概括方法；數軸的建立是對生活模型的類比，可以滲透數學的模型思想和類比思想；數軸本身就是數與形的充分結合，在教學中需要向學生傳達數形結合的思想方法.

數軸概念的概括過程，需充分利用溫度計，從溫度計的0度、單位長度、直線方向等方面進行抽象，確保概括過程的完整性、合理性和準確性.而在概括的最后階段，需要引導學生利用數學語言描述數軸，即從數軸建立的三要素來表述，使學生充分學習知識從生活經驗中抽象、概括的方法，也可以結合具有辨析性的數軸問題，檢驗學生抽象概括過程的理解程度.

圖5

在利用溫度計建立數軸過程中，要充分滲透模型思想，即從生活中的原模型——溫度計，建立研究問題的數學模型——數軸，然后利用數軸研究問題，實現模型思想的雙向傳遞.對于數軸上的大小關系，則可以滲透類比思想，如給出溫度計與數軸的對應圖，如圖5，讓學生思考溫度計由上到下的數值變化關系，以及數軸由左到右的變化情況，并比較點的位置關系.類比溫度計的溫度變化，學生可以較為容易地得出數軸上兩點的大小關系，右邊表示的數必然比左邊表示的數大，則從左到右是逐漸增大的過程，滲透類比思想更能輔助學生進行規律總結.

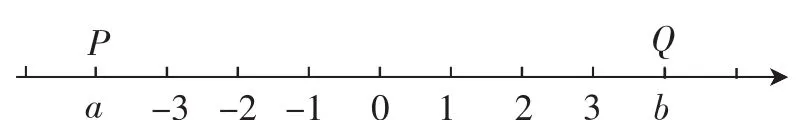
圖6

數軸實現了數與點的對應，這是一種較為特殊的數形對應，因此對于數軸的深入教學需要滲透數形結合思想，即不僅從圖像角度使學生了解點之間的位置關系，還需要從代數方面使學生理解數的大小關系.如在教學中設置如下問題：圖6所示數軸上的點P坐標為a，點Q的坐標為b，則P和Q兩點之間的距離如何表示？該問題表面上是數軸上兩點之間的距離表示，實際上是數學的代數運算問題，結合數軸的正方向的唯一性，很容易可得b＞a，則PQ=b－a.單純依靠代數分析并不能確定b和a的大小關系，結合數軸圖則可以避開分類討論，完成數學符號的關系表述，實現距離的精準求解，兩者的充分結合充分體現出數形結合的思想意義.

在教學中滲透數學的思想方法，注重培養學生的思維能力，是新課改對于中學教學的思想要求.思想是數學的精髓，依托于知識內容，而又需要以具體的方式向學生傳達，“數軸”的教學中采用結合實際問題、特殊情形，引導思考的方式，更能使學生親身體會思想方法的重要意義，在潛移默化中獲得思想的提升.

四、結束語

“數軸”內容對于學生而言并不陌生，但如何使學生在原有基礎上獲得更深的知識感悟則存在一定的難度，最有效的方法是依托學生已有的經驗基礎，結合基本的實踐活動，引導學生體驗概念形成的初始階段，從中歸納數軸的基本規律；緊抓數軸的“表示”要義，設置具體的問題情景，引導學生思考分析，充分理解數軸上點對數的完整表示.數軸作為具有重要教學啟示的內容，還肩負著提升學生思想的重任，在教學中需滲透抽象思想、概括方法、模型思想、類比思想、數形結合思想，以全面提升學生的思想水平為教學目標，達成素質教育的偉大愿景.

1.史承灼，謝衛松.層層遞進巧設問 循循善誘究真知——探究課“數軸的再認識”的問題賞析［J］.中學數學（下），2017（11）.

2.王秀梅.習題課教學：從“拿來主義”走向編題變式——以“數軸再認識”習題課為例［J］.中學數學（下），2016（10）.

3.呂娟.數軸在初中數學教學中的妙用［J］.中學數學教學參考，2017（36）.

4.徐沙沙.“數軸”單元的教學設計與思考——蘇科版七年級上冊數軸1課時［J］.數理化學習，2016（12）.F