拋物線“牽手”幾何圖形為哪般

☉江蘇省南京市竹山中學(xué) 黃秀旺

二次函數(shù)是初中數(shù)學(xué)的重點內(nèi)容之一，每年全國各地的中考試卷中都會出現(xiàn)以二次函數(shù)為背景的解答題，其綜合性較強(qiáng)，難度較高.其中，有些問題借助拋物線上一個點或兩個點，討論三角形或四邊形的形狀或圖形之間的關(guān)系，此時可以“拿掉”拋物線，似有“假二次函數(shù)問題”之嫌；還有一類問題，將拋物線的“軸對稱性”與幾何圖形（軸對稱圖形）的“軸對稱性”相結(jié)合，其構(gòu)思巧妙又不失自然與合理，將函數(shù)圖像與幾何圖形因軸對稱之緣而“牽手”，凸顯拋物線的軸對稱性，滲透數(shù)形結(jié)合、幾何直觀的數(shù)學(xué)思想方法.解決此類問題就是要將圖像的對稱性與圖形的對稱性結(jié)合起來，從對稱性的角度進(jìn)行推理，發(fā)現(xiàn)新結(jié)論.

一、好題賞析

例1如圖1，已知拋物線y=ax2+bx+c經(jīng)過A（1，0）、B（4，0）、C（0，3）三點.

（1）求拋物線的解析式.

（2）如圖1，在拋物線的對稱軸上是否存在點P，使得PA+PC最小？若存在，求出PA+PC的最小值；若不存在，請說明理由.

分析：（1）設(shè)拋物線的解析式為y=a（x－1）（x－4），把C（0，3）代入得a·（－1）·（－4）=3，解得，所以拋物線的解析式為，即

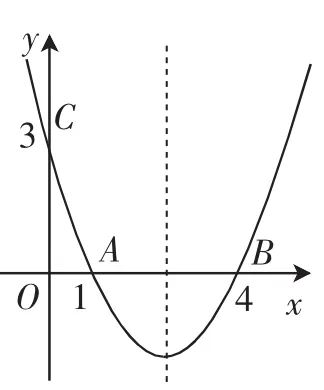
圖1

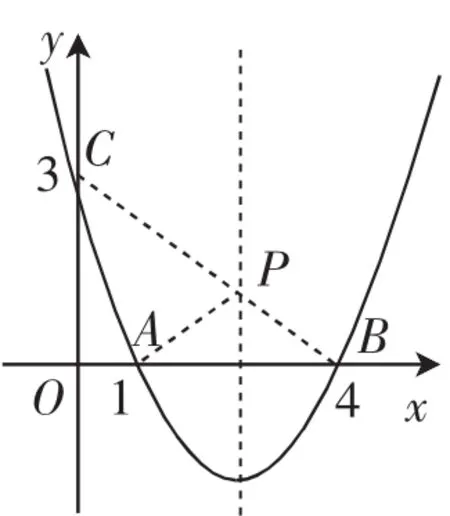
圖2

解：（1）略.

（2）存在.因為A（1，0）、B（4，0），所以拋物線的對稱軸為直線

連接BC交直線于點P，如圖2，則PA=PB，PA+PC=PC+PB=BC，此時PC+PA最短，因為所以PA+PC的最小值為5.

拓展1：如圖2，在拋物線的對稱軸上是否存在點P，使得四邊形PAOC的周長最小？若存在，求出四邊形PAOC周長的最小值；若不存在，請說明理由.

拓展2：如圖2，在拋物線的對稱軸上是否存在點P，使得拋物線的對稱軸平分∠CPB？若存在，求出點P的坐標(biāo)；若不存在，請說明理由.

點評：例1中的第（2）小題是典型的“將軍飲馬”問題，通常我們需要作點A關(guān)于一條直線的對稱點；拓展1求四邊形PAOC周長的最小值，其本質(zhì)仍是PA+PC取最小值；拓展2通過問題轉(zhuǎn)化，需作點B關(guān)于直線的對稱點（即點A），連接CA并延長，直線CA與直線的交點即為點P.從以上分析發(fā)現(xiàn)，問題解決需運用拋物線的對稱性，由于點A與點B關(guān)于直線對稱，所以無需作圖就可得到點A（或點B）的對稱點，以上拓展問題凸顯了拋物線的對稱性.

例2某水渠的橫截面呈拋物線形，水面的寬為AB（單位：m）.現(xiàn)以AB所在直線為x軸，以拋物線的對稱軸為y軸建立如圖3所示的平面直角坐標(biāo)系，設(shè)坐標(biāo)原點為O.已知AB=8m.設(shè)拋物線的解析式為y=ax2－4.

（1）求a的值；

（2）C（－1，n）是拋物線上一點，點C關(guān)于原點O的對稱點為點D，連接CB、BD、DC，求△BCD的面積.

分析：（1）因為AB=8，由拋物線的對稱性可知OB=4，所以B（4，0），0=16a－4，所以（.2）把C點坐標(biāo)代入解析式，求得n的值，再根據(jù)D、C關(guān)于原點對稱求出點D坐標(biāo)，然后根據(jù)求出面積即可.

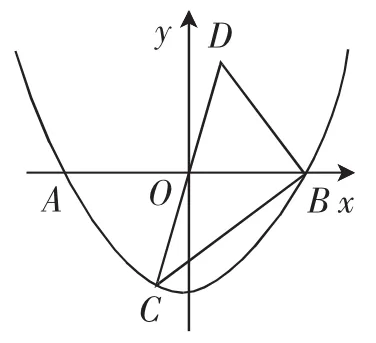
圖3

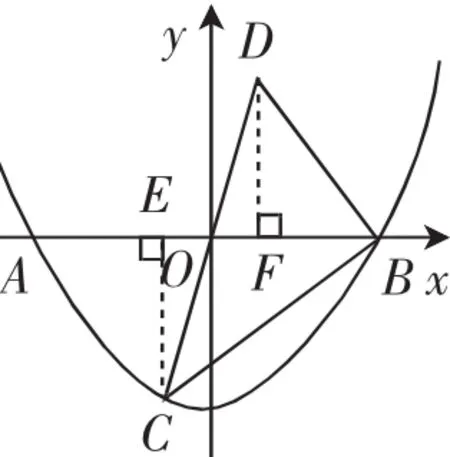
圖4

解：（1）略.

（2）過點C作CE⊥AB于點E，過點D作DF⊥AB于點F，如圖4所示.

由（1）知

令x=-1，得，所以

因為點C關(guān)于原點的對稱點為點D，所以

所以

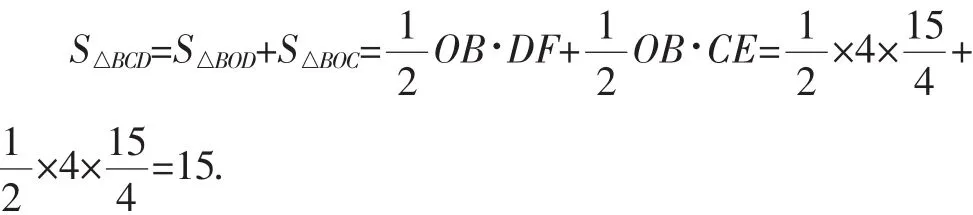
所以△BCD的面積為15m2.

拓展1：求四邊形ACBD的面積.

拓展2：如果C是拋物線上一個動點，點C關(guān)于原點O的對稱點為點D，連接AC、CB、BD、DA，那么是否存在四邊形ACBD是矩形？若存在，求出點C的坐標(biāo)；若不存在，請說明理由.

拓展3：對于拋物線y=ax2+c（a≠0），它與x軸交于點A、B，C是拋物線上一個動點，點C關(guān)于原點O的對稱點為點D，連接AC、CB、BD、DA，是否存在四邊形ACBD是正方形？請?zhí)骄縜與c之間的數(shù)量關(guān)系.

拓展4：對于拋物線y=ax2+bx+c（a≠0），它與x軸交于點A、B，C是拋物線上一個動點，點C關(guān)于點）的對稱點為點D，連接AC、CB、BD、DA，是否存在四邊形ACBD是正方形？請?zhí)骄縜、b、c之間滿足的數(shù)量關(guān)系.

點評：“點C關(guān)于原點O的對稱點為點D”為題目給出的條件，結(jié)合拋物線的對稱性，點A與點B關(guān)于y軸所在直線對稱，由此可以推測點A與點B關(guān)于原點O對稱，從而可以判定四邊形ACBD是平行四邊形.接下來的拓展1、拓展2、拓展3進(jìn)一步討論四邊形ACBD的面積，以及它是否可以為矩形、正方形，特別是探究正方形時，將充分關(guān)注拋物線的對稱性與正方形的對稱性，并且它們有一條對稱軸是相同的.

例3如圖5，直線y=－3x+3與x軸、y軸分別交于點A、B，拋物線y=a（x－2）2+k經(jīng)過點A、B，并與x軸交于另一點C，其頂點為P.

（1）求a，k的值；

（2）在拋物線及其對稱軸上分別取點M、N，使以A，C，M，N為頂點的四邊形為正方形，求此正方形的邊長.

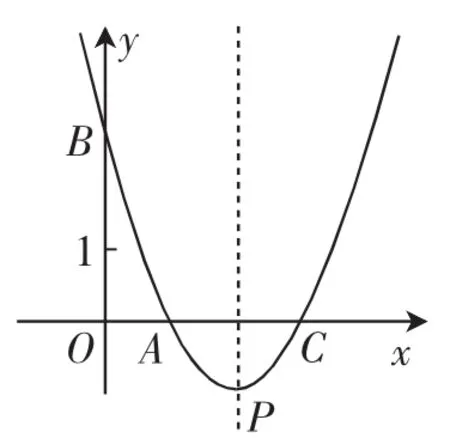
圖5

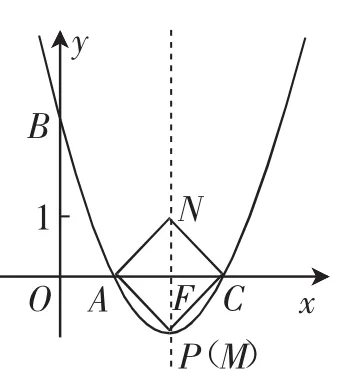
圖6

分析：（1）因為直線y=－3x+3與x軸、y軸分別交于點A、B，所以A（1，0），B（0，3）.又拋物線y=a（x－2）2+k經(jīng)過點A（1，0），B（0，3），所以解得即a，k的值分別為1，－1.（2）如圖6，當(dāng)點N在對稱軸上時，由NC與AC不垂直，得出AC為正方形的對角線，根據(jù)拋物線的對稱性及正方形的性質(zhì)，得到M點與頂點P（2，－1）重合，N點為點P關(guān)于x軸的對稱點，此時，MF=NF=AF=CF=1，且AC⊥MN，則四邊形AMCN為正方形.在Rt△AFN中，根據(jù)勾股定理即可求出正方形的邊長.

解：（1）略.

（2）當(dāng)點N在對稱軸上時，NC與AC不垂直.所以AC應(yīng)為正方形的對角線.又對稱軸x=2是AC的中垂線，所以M點與頂點P（2，－1）重合，N點為點P關(guān)于x軸的對稱點，其坐標(biāo)為（2，1）.此時MF=NF=AF=CF=1，且AC⊥MN，所以四邊形AMCN為正方形.

在Rt△AFN中，即正方形的邊長為

拓展1：是否存在⊙P，使得⊙P經(jīng)過點A、C，且與y軸相切？若存在，請求出點P的坐標(biāo)；若不存在，請說明理由.

點評：例3緊扣正方形的性質(zhì)，從點A與點C之間的關(guān)系，以及AC的長，結(jié)合拋物線的對稱性推出M點與N點之間的關(guān)系及其位置；拓展1將圓的對稱性與拋物線的對稱性結(jié)合起來，從“⊙P經(jīng)過點A、C”結(jié)合圓的對稱性可以判斷圓心P在直線x=2上.

例4如圖7，已知二次函數(shù)y=x2－2x－1的圖像的頂點為A.二次函數(shù)y=ax2+bx的圖像與x軸交于原點O及另一點C，它的頂點B在函數(shù)y=x2－2x－1的圖像的對稱軸上.

（1）求點A與點C的坐標(biāo)；

（2）當(dāng)四邊形AOBC為菱形時，求函數(shù)y=ax2+bx的關(guān)系式.

分析：（1）因為y=x2－2x－1=（x－1）2－2，所以頂點A的坐標(biāo)為（1，－2）.因為二次函數(shù)y=ax2+bx的圖像與x軸交于原點O及另一點C，它的頂點B在函數(shù)y=x2－2x－1的圖像的對稱軸上，所以二次函數(shù)y=ax2+bx的對稱軸為直線x=1，所以點C和點O關(guān)于直線x=1對稱，所以點C的坐標(biāo)為（2，0）.（2）因為四邊形AOBC是菱形，根據(jù)菱形的性質(zhì)，可以得出點O和點C關(guān)于直線AB對稱，點B和點A關(guān)于直線OC對稱，因此可求出點B的坐標(biāo).根據(jù)二次函數(shù)y=ax2+bx的圖像經(jīng)過點B（1，2），C（2，0），將B，C代入解析式得出a、b的值，進(jìn)而得出其解析式.

解：（1）略.

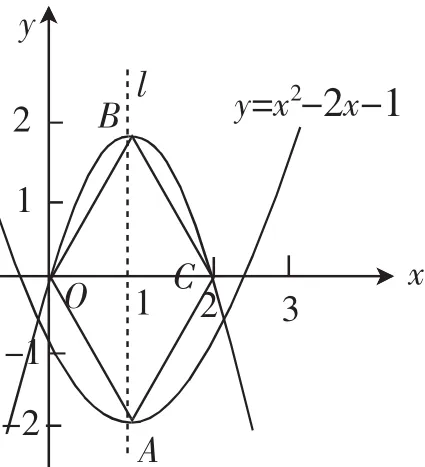
圖7

（2）因為四邊形AOBC是菱形，所以點B和點A關(guān)于直線OC對稱，因此點B的坐標(biāo)為（1，2）.

因為二次函數(shù)y=ax2+bx的圖像經(jīng)過點B（1，2），C（2，0），所以解得所以y=－2x2+4x.

拓展1：當(dāng)四邊形AOBC的面積為6時，求函數(shù)y=ax2+bx的關(guān)系式.

拓展2：當(dāng)以點A、O、B、C為頂點構(gòu)成的四邊形的面積為6時，求函數(shù)y=ax2+bx的關(guān)系式.

拓展3：觀察拓展1和拓展2所求得的函數(shù)關(guān)系式，并結(jié)合其圖像的位置，請你再寫一個與它們有共同特點的函數(shù)關(guān)系式.

點評：第（2）小題，從二次函數(shù)y=ax2+bx的圖像性質(zhì)可知，點O與點C關(guān)于直線AB對稱，而當(dāng)四邊形AOBC是菱形時，點O與點C也是關(guān)于直線AB對稱的，所以函數(shù)y=ax2+bx的對稱軸就是菱形AOBC的一條對角線所在的直線，進(jìn)而確定點B的位置；拓展1與拓展2都關(guān)注點O與點C關(guān)于直線AB對稱，從而過點A、B的直線垂直O(jiān)C，而四邊形的面積可以改變，但是拋物線y=ax2+bx經(jīng)過點O、C則是不變的，解題的關(guān)鍵是確定點B的坐標(biāo).

二、感悟與歸納

等腰三角形、菱形、正方形、等腰梯形、圓等都是軸對稱圖形，而拋物線也具有軸對稱性，因此，有些試題可以將拋物線與幾何圖形結(jié)合起來，一方面，通過拋物線的對稱性容易獲得圖像上一個點的對稱點，為進(jìn)一步探究幾何圖形的形狀提供條件；另一方面，幾何圖形的對稱性也可以確定相關(guān)線段的長度，進(jìn)而確定圖像上點的坐標(biāo)，所以拋物線“牽手”幾何圖形為哪般呢，原因在于它們都具有軸對稱性！ H