代數(shù)法：易想難算 幾何法：多思少算

☉江蘇省啟東市折桂中學(xué) 趙春風(fēng)

在數(shù)學(xué)問題解決過程中，我們時(shí)常會(huì)發(fā)現(xiàn)有的問題既可以從代數(shù)的角度進(jìn)行解答，又可以從幾何的角度進(jìn)行解答，而兩種方法中有時(shí)各有千秋，有時(shí)平分秋色.本文呈現(xiàn)兩則案例，分別從代數(shù)和幾何的角度給出解答，并進(jìn)行簡(jiǎn)單的分析，同時(shí)對(duì)案例2進(jìn)行簡(jiǎn)單改編，不當(dāng)之處，敬請(qǐng)指正.

案例1（根據(jù)2016年煙臺(tái)卷第25題第（3）問改編）如圖1，點(diǎn)A的坐標(biāo)為（2，6），點(diǎn)C的坐標(biāo)為（4，3），過點(diǎn)A、C的直線分別與x軸的正半軸、y軸的正半軸交于點(diǎn)H、G，P是直線AC上的任意一點(diǎn)，設(shè)其橫坐標(biāo)為m，過點(diǎn)P向x軸和y軸分別作垂線，垂足分別為M和N，連接MN，求線段MN的最小值并給出此時(shí)m的值.

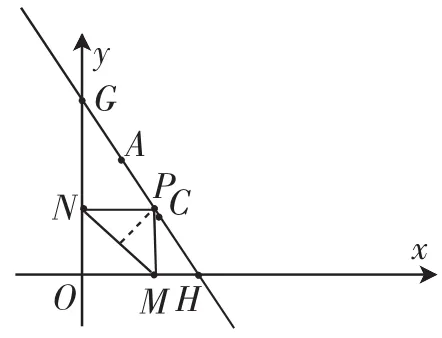
圖1

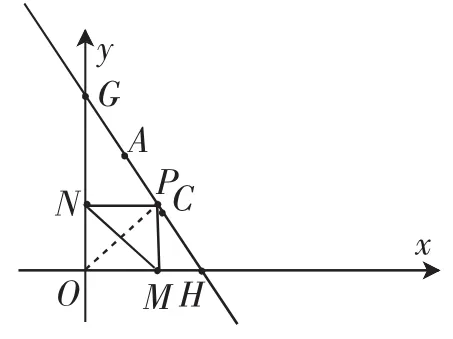
圖2

方法1：（代數(shù)法）由待定系數(shù)法得過點(diǎn)A、C的直線的方程為于是可設(shè)點(diǎn)P的坐標(biāo)為），進(jìn)而可得點(diǎn)M的坐標(biāo)為（m，0），點(diǎn)N的坐標(biāo)為），所以，所以當(dāng)時(shí)，MN2取到最小值，即MN的最小值為

方法2：（幾何法）由待定系數(shù)法得過點(diǎn)A、C的直線的方程為所以O(shè)H=6，OG=9.

由題意得MN=OP，顯然當(dāng)OP⊥HG時(shí)（如圖2），線段OP的長(zhǎng)度最小，即此時(shí)所以

所以MN的最小值為，此時(shí)

方法1從代數(shù)的角度給出，可以看出思路非常自然，然而計(jì)算過程比較復(fù)雜，在考試過程中可能很難得到正確的答案.方法2從幾何的角度給出解答，整個(gè)求解過程計(jì)算簡(jiǎn)單，利用了點(diǎn)與線之間，垂線段最短，以及“面積相等算兩次”的基本方法，但是有一定的思維含量，特別是學(xué)生可能很難求出m的值，因?yàn)閷W(xué)生很難與相似三角形或銳角三角函數(shù)產(chǎn)生聯(lián)系，如果從這個(gè)角度看的話就不如方法1了，方法1可以說是一箭雙雕，在得到MN的最小值的同時(shí)也得到了m的值.

案例2如圖3，△ABC是邊長(zhǎng)為4的等邊三角形，D是邊BC上的任意一點(diǎn)，連接AD，作線段AD的垂直平分線交邊AC于點(diǎn)N，求線段CN的最大值.

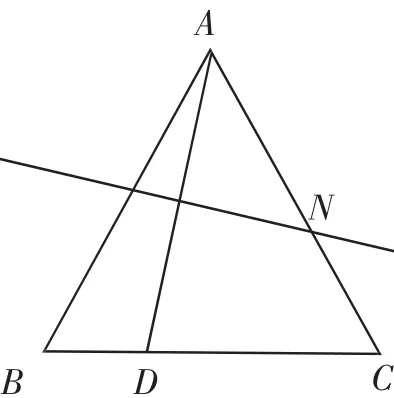
圖3

圖4

方法1：（代數(shù)法）如圖4，連接MD、ND，則△BMD∽△CDN.

設(shè)BD=x（0≤x≤4），CN=y，則△BMD的周長(zhǎng)為4+x，△CDN的周長(zhǎng)為8－x，根據(jù)相似三角形的性質(zhì)（相似三角形的相似比等于周長(zhǎng)比）得，解得

令 t=4+x， 則 4 ≤t≤8， 所 以，即當(dāng)，也就是說當(dāng)時(shí)，y取到最大值，所以線段CN的最大值為

方法2：（幾何法）如圖5，連接ND，過點(diǎn)N作NP⊥BC，垂足為P.

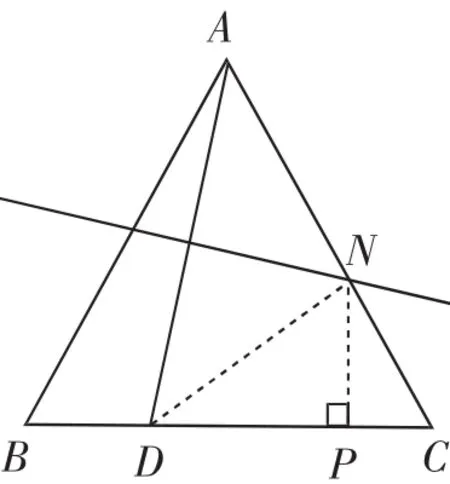
圖5

于是當(dāng)DN與NP重合（DN=NP）時(shí)，線段CN取到最大值

方法1中學(xué)生比較容易發(fā)現(xiàn)圖形中的相似三角形（一線三等角），此時(shí)學(xué)生很容易陷入誤區(qū)，僅僅考慮到“相似三角形的對(duì)應(yīng)邊成比例”，而忽略了“相似三角形的周長(zhǎng)比等于相似比”這一重要的性質(zhì)，導(dǎo)致學(xué)生不能得到正確的關(guān)系式.即使有的學(xué)生可以得到正確的關(guān)系式，也不可能求出最大值，這里用到了高中階段的均值不等式，需要注意滿足“一正、二定、三相等”，如果從這個(gè)角度考慮的話這應(yīng)該不是命題人的本意.方法2從幾何的角度出發(fā)，具有一定的技巧性，應(yīng)用“直角三角形的斜邊大于直角邊”這一事實(shí)進(jìn)行求解，也很難想到.說實(shí)話，這種方法對(duì)于學(xué)生而言應(yīng)該是很難想到的，大多數(shù)的老師應(yīng)該也在其中（筆者是在用幾何畫板演示過程中發(fā)現(xiàn)當(dāng)DN與NP重合時(shí)，CN取到最大值，才有了上述的方法2）.

下面針對(duì)上述問題對(duì)案例2進(jìn)行簡(jiǎn)單改編（題干不變）：

（1）如圖4，連接MD、ND，證明△BMD∽△CDN；

（2）設(shè)BD=x，CN=y，請(qǐng)給出y與x的函數(shù)關(guān)系式并寫出自變量x的取值范圍；

（3）設(shè)（2）中得到的函數(shù)在自變量取值范圍內(nèi)的最大值為m，請(qǐng)直接寫出點(diǎn)D從點(diǎn)B移動(dòng)到點(diǎn)C的過程中，點(diǎn)N在邊AC上移動(dòng)路徑的長(zhǎng)度共為多少？（用含m的代數(shù)式進(jìn)行表示）

參考答案：（1）（2）略.（3）2m－2.

上述試題的改編?kù)`感來自于下述兩題：

題1：（2017年東營(yíng)卷第24題）如圖6，在等腰三角形ABC中，∠BAC=120°，AB=AC=2，D是邊BC上的一點(diǎn)（不與點(diǎn)B、C重合），在AC上取一點(diǎn)E，使∠ADE=30°.

（1）求證：△ABD∽△DCE；

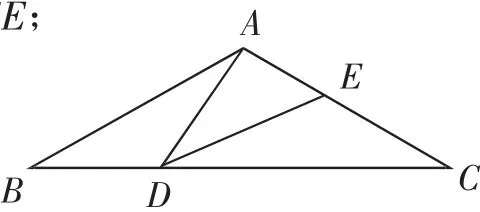
圖6

（2）設(shè) BD=x，AE=y，寫出y與x的函數(shù)關(guān)系式，并寫出自變量x的取值范圍；

（3）略.

題2：（2017年嘉興卷第16題）如圖7，一副含30°和45°角的三角板ABC和DEF疊合在一起，邊BC與EF重合，BC=EF=12cm，G為邊BC（EF）的中點(diǎn)，邊FD與AB相交于點(diǎn)H，此時(shí)線段BH的長(zhǎng)是.現(xiàn)將三角板DEF繞點(diǎn)G按順時(shí)針方向旋轉(zhuǎn)，如圖8，在∠CGF從0°到60°的變化過程中，點(diǎn)H相應(yīng)移動(dòng)的路徑長(zhǎng)共為（結(jié)果保留根號(hào)）

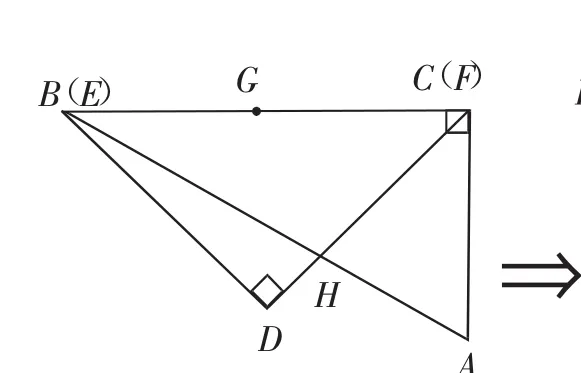
圖7

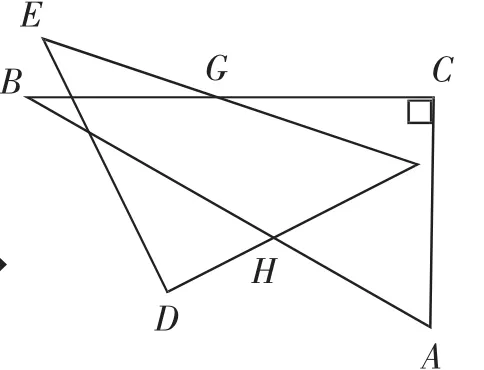
圖8

通過上面的介紹可以看出，代數(shù)法需要通過構(gòu)造函數(shù)關(guān)系，進(jìn)而將問題解決；幾何法則需要用到垂線段最短（案例1），直角三角形中斜邊大于直角邊（案例2）.當(dāng)然見的最多的可能是兩點(diǎn)之間線段最短（將軍飲馬問題），以及圓上動(dòng)點(diǎn)與圓外定點(diǎn)之間距離的最大值和最小值等問題.可以說兩種方法各有千秋，甚至平分秋色；但是，筆者認(rèn)為“代數(shù)法：易想難算，幾何法：多思少算”.H