巧用幾何性質(zhì)，多解深剖釋疑
——以一道平面幾何題為例

☉江蘇省常熟市海虞中學(xué) 顧雅玉

對幾何考題開展一題多解不僅可以多角度認(rèn)識問題，挖掘圖形性質(zhì)，還可以拓展解題思路，提升對數(shù)學(xué)問題的剖析能力.以一道平面幾何題為例進(jìn)行多解剖析，并從挖掘性質(zhì)條件、夯實(shí)知識基礎(chǔ)、滲透思想方法等方面開展教學(xué)反思，從而引導(dǎo)學(xué)生在反思的過程中提升解題素養(yǎng).

一、問題呈現(xiàn)

1.考題呈現(xiàn)

題目如圖1，AB是⊙O的直徑，且AB與弦CD垂直于點(diǎn)E，連接CO，并將其延長，交弦AD于點(diǎn)F，已知CF⊥AD，AB=2，試求弦長CD的長.

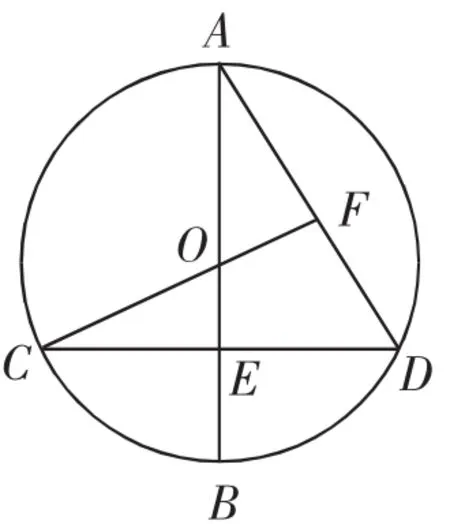
圖1

2.思路突破

本題目為初中常見的涉及圓的幾何題，主要考查學(xué)生三角形、圓等圖形的基本知識，整理題干信息可得以下關(guān)鍵條件：有一條直徑（AB）；兩個(gè)垂直關(guān)系（AB⊥CD、CF⊥AD）；一條線段長（AB=2）.需要建立條件與待求量CD之間的關(guān)系，觀察圖形可知點(diǎn)A、C、D均位于⊙O上，則連接AC后，△ACD的外接圓是⊙O，利用不同的幾何性質(zhì)即可建立已知與未知之間的關(guān)系.

二、解法剖析

圓和三角形存在諸多的性質(zhì)，利用不同的性質(zhì)，從不同的角度分析問題，往往可以獲得不同的解題方法，以下將具體剖析本題目不同視角下的不同解法.

視角一：利用等腰三角形的“三線合一”

由于題目中存在等腰三角形，可以利用等腰三角形“三線合一”的性質(zhì)來求解，即等腰三角形中頂角的角平分線、底邊上的中線和底邊上的高三條線是相互重合的，只需確定其中的一條線即可推得等腰三角形的其他性質(zhì).

分析1：在△ACD中，AE⊥CD，由于AB過圓心O，可以推斷出AB是CD的垂直平分線，利用垂直平分線的性質(zhì)可進(jìn)一步推得AC=AD，則△ABC是等腰三角形，利用CF⊥AD，同理可得AC=CD，則△ACD就是等邊三角形，其每個(gè)內(nèi)角都為60°.AB為直徑，則半徑CO=1，結(jié)合“三線合一”性質(zhì)可推得△COE的內(nèi)角，進(jìn)而可得CD的長.

解法1：連接AC，如圖2，因?yàn)锳B⊥CD，且AB過圓心O，則CE=DE，所以AB是CD的垂直平分線，則AC=AD；同理由CF⊥AD可得AC=CD，所以△ACD是等邊三角形.由于CF是△ACD底邊AD上的中線和高，由“三線合一”可知CF必為∠ACD的平分線，則∠FCD=30°，因?yàn)椋?/p>

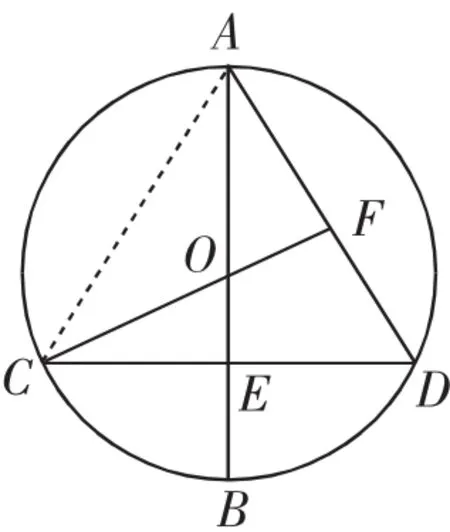
圖2

點(diǎn)評：等腰三角形的“三線合一”既是對三角形特征的一種簡單概述，也是一種幾何性質(zhì)，由于涉及角平分線、中線和高，則可以通過確定線段具有其中的一種性質(zhì)來推得其他幾何性質(zhì)，上述解題思路就是通過確定中線和高來推得等邊三角形角平分線的性質(zhì)，從而打開解題思路的，需要注意的是“三線合一”只適用于等腰三角形，這是使用的基本條件.

視角二：利用三角形“重心”的性質(zhì)

根據(jù)題目的相關(guān)條件可以預(yù)判圖中出現(xiàn)了△ACD的多條中線，則可以利用三角形的重心（三角形三條中線的交點(diǎn)為重心）性質(zhì)來求解，即重心分別到三角形頂點(diǎn)和對邊中點(diǎn)的距離之比為2：1，則可以建立三角形中相關(guān)線段的長度關(guān)系.

分析2：根據(jù)條件可得出AE、CF分別為△ACD的邊CD和AD的中線，進(jìn)而可確定O為三角形的重心，利用重心的性質(zhì)可得AO、OE的長度，然后在Rt△OCE中，利用勾股定理可得CE的長，從而求得CD.

解法2：因?yàn)锳B⊥CD、CF⊥AD，且AB、CF均過圓心O，則CE=DE，AF=DF，即AE是△ACD的邊CD上的中線，CF是△ACD的邊AD上的中線，所以點(diǎn)O為三角形的重心，則AO=2OE.已知在Rt△OCE中

點(diǎn)評：三角形的重心是其三條中線的交點(diǎn)，利用其性質(zhì)可以實(shí)現(xiàn)幾何特征向幾何元素邊長之間的條件轉(zhuǎn)化，由于兩條線即可確定一個(gè)交點(diǎn)，因此在實(shí)際應(yīng)用中只需要確定三角形任意的兩條中線即可，中線的確定方式有很多，可以通過線段的垂直平分線、全等三角形對應(yīng)邊相等，以及圓心對直徑的分割等條件來確定，上述解題過程就是利用圓內(nèi)弦長及相關(guān)線段的垂直關(guān)系來確定中線的，具體解題時(shí)需靈活運(yùn)用.

視角三：利用菱形的相關(guān)性質(zhì)

題目中存在線段垂直和相等等相關(guān)信息，則可以在圖形中構(gòu)造一個(gè)菱形，利用菱形的相關(guān)性質(zhì)，如對角線相互垂直且平分、四條邊均相等來嘗試構(gòu)建已知條件與待求量之間的關(guān)系.構(gòu)建菱形時(shí)需要注意一定的方式，力求利用最少的條件來完成，如先確定四邊形是平行四邊形，再確定其為菱形.

分析3：連接OD、CB、DB后可以通過三角形全等來證明四邊形CBDO為平行四邊形，再通過一條鄰邊相等即可證明其為菱形，利用菱形的性質(zhì)可以得到線段OE的長，在Rt△OCE中利用勾股定理即可求出CE的長，進(jìn)而求得CD.

解法3：連接OD、CB、DB，如圖3，由已知條件可得△CEO≌△DEB，則OC=BD，∠OCE=∠BDE，可得OC∥BD.因?yàn)镺C=BD且OC∥BD，可得四邊形CBDO為平行四邊形.又因?yàn)镃O=DO，可知四邊形CBDO為菱形，可得

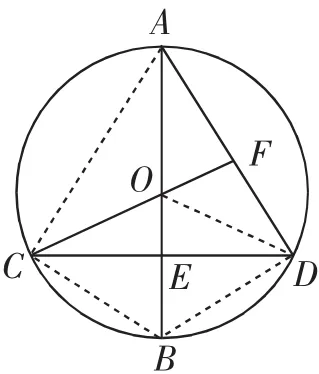
圖3

.在Rt△OCE中，CO=

點(diǎn)評：菱形是一種較為特殊的平行四邊形，因此其除具有平行四邊形的有關(guān)性質(zhì)以外還有一些自身特有的性質(zhì)，這些性質(zhì)除可以證明其為菱形以外，也可以用于幾何相關(guān)問題的證明.一般菱形的證明需要先確定四邊形是平行四邊形，再通過確定一條鄰邊相等或?qū)蔷€相互垂直來完成.

視角四：利用代數(shù)方程求解

初中數(shù)學(xué)最為常見的方法是數(shù)形結(jié)合的方法，其解題思路是利用直觀圖形來分析幾何關(guān)系，然后利用代數(shù)的精準(zhǔn)性來建立反映幾何關(guān)系的方程，這種方程就是研究幾何問題的一種數(shù)學(xué)模型，本題目求幾何線段，可以設(shè)出未知數(shù)，利用相關(guān)性質(zhì)來建立關(guān)于線段的方程，通過求方程的解來完成.

分析4：可證明△COE和△ADE相似，利用相似性質(zhì)可建立對應(yīng)邊之間的關(guān)系，然后設(shè)出未知數(shù)CE=x，由勾股定理可得OE，結(jié)合相似建立的邊長關(guān)系可建立一個(gè)關(guān)于線段長度的方程，解方程后即可求解.

解法4：因?yàn)锳B⊥CD,CF⊥AD，則∠OCE+∠COE=90°.∠AOF+∠OAF=90°. 又因?yàn)椤螦OF=∠COE，所以∠OCE=∠OAF，則△COE∽△ADE，則.設(shè)CE=x，則，解得，所以

點(diǎn)評：利用代數(shù)方程求解實(shí)質(zhì)上是建立了研究幾何問題的一種數(shù)學(xué)模型，其依然是基于對幾何圖形的關(guān)系分析，如上述求解時(shí)利用到了三角形相似及勾股定理等性質(zhì).代數(shù)方程的建立使得問題變得更為簡單直接，僅通過方程求解就可以求出線段的長，因此可以有效提高解題效率.

三、反思與啟示

1.挖掘性質(zhì)條件，強(qiáng)化知識理解

初中數(shù)學(xué)的幾何題有著其自身獨(dú)有的特點(diǎn)，從不同的角度分析問題往往可以得到不同的性質(zhì)條件，從而獲得不同的解題思路，而不同的解題方法往往可以得到同一個(gè)答案，實(shí)現(xiàn)問題的殊途同歸.上述分析線段長分別從三角形的“三線合一”、重心性質(zhì)、菱形性質(zhì)和代數(shù)方程等角度來求解，均是從不同的角度對問題的分析，其思路是建立在幾何性質(zhì)的充分挖掘上.在實(shí)際教學(xué)中開展一題多解，不僅是要使學(xué)生掌握多種解法，還是為了引導(dǎo)學(xué)生多角度的挖掘幾何性質(zhì)，能夠靈活運(yùn)用幾何知識來求解，從而強(qiáng)化學(xué)生對于知識的理解.

2.夯實(shí)基礎(chǔ)知識，掌握知識綜合

上述的幾何問題涉及了三角形、圓等基本的圖形，是多圖形的交叉組合，求解過程也是對相關(guān)性質(zhì)的綜合運(yùn)用，看似復(fù)雜實(shí)質(zhì)解法有跡可循，即充分挖掘問題的基本圖形，將復(fù)合圖形分解為單一的基本圖形，然后分別利用圖形的基本性質(zhì)來求解，若圖形較為抽象，可以通過添加輔助線的方式，使其變?yōu)楹唵螆D形.如上述問題的解法均是利用三角形、圓或菱形的性質(zhì)來求解，均是對基本性質(zhì)、基本定理和基本方法的綜合運(yùn)用，因此在實(shí)際教學(xué)中需要引導(dǎo)學(xué)生掌握幾何提煉的相關(guān)方法，夯實(shí)基本的單體知識，然后從知識綜合性角度出發(fā)對單體知識進(jìn)行綜合運(yùn)用，從而掌握復(fù)雜幾何問題的解題策略.

3.滲透思想方法，提升解題能力

上述問題的求解涉及了多種方法，解法中同樣滲透著多種解題思想，如輔助線的添加涉及了構(gòu)造思想、圖形問題的求解涉及了數(shù)形結(jié)合思想、代數(shù)方程法涉及了方程思想，整個(gè)解題過程不僅是方法技巧的運(yùn)用，同樣貫穿著多種思想的活動(dòng)，是解題的思想方法在指引著問題的轉(zhuǎn)化變形.可以這么說，一題多解不僅是一種方法的多解，也是思想的多解.因此，在實(shí)際教學(xué)中，要結(jié)合具體問題向?qū)W生滲透解題的思想方法，使學(xué)生在掌握解題策略的同時(shí)獲得思想上的提升，從而從本質(zhì)上提升學(xué)生解決問題的素養(yǎng)和能力.

四、結(jié)束語

幾何作為初中數(shù)學(xué)的重要內(nèi)容，其考題也是中考的重要題型.對其開展一題多解訓(xùn)練有著深層的意義，不僅可以多角度挖掘圖形性質(zhì)，強(qiáng)化知識理解，還可以拓展解題思維.在教學(xué)中要引導(dǎo)學(xué)生夯實(shí)基礎(chǔ)，綜合運(yùn)用知識，考題講解中滲透思想方法，使學(xué)生達(dá)到能力與素養(yǎng)的真正提升.

1.董海榮.深入挖掘結(jié)論，逐層拓展應(yīng)用——以中考幾何探究題為例［J］.中學(xué)數(shù)學(xué)（下），2018（4）.

2.劉華為，余利英.基于轉(zhuǎn)化思想，探求一題多解［J］.中學(xué)數(shù)學(xué)（下），2016（8）.

3.謝良毅.知識綜合巧運(yùn)用，一題多解闊思維——以一道初中平面幾何題為例［J］.中學(xué)數(shù)學(xué)教學(xué)參考，2018（Z3）.

4.黃勇慶.一題多層面，多解化幾何［J］.中學(xué)數(shù)學(xué)教學(xué)參考，2017（33）.H