探尋問題本質，變式學習探究
——以一道函數綜合題為例

☉蘇州高新區實驗初級中學 楊 穎

中考函數壓軸題以綜合題居多，圖像涉及眾多函數，求解時需要深入探尋問題本質，采用適當的方法，對問題的條件進行轉化，然后利用基本性質來求解.本文將詳細講解一道中考函數綜合題的解題思路，并對其進行解讀變式，開展教學思考，以供讀者交流學習.

一、考題呈現及思路突破

1.考題呈現

題目（2016年江蘇泰州中考數學卷第24題）如圖1所示，反比例函數上存在A、B兩點，坐標分別為A（m，4），B（－4，n），現經過點A、B作一直線，與x軸相交于點C，與y軸相交于點D，試求下列問題：

（1）如果m=2，求n的具體值；

（2）試求m+n的值；

（3）現連接OA、OB，如果tan∠AOD+tan∠BOC=1，求直線AB的函數解析式.

2.思路突破

分析：（1）m=2，則點A（2，4），反比例函數只有一個未知數k，只需一個點即可確定具體的函數解析式，點B位于反比例函數上，則其坐標必然滿足反比例函數解析式，可以將其點坐標代入求解；（2）求m+n的值，需要先確定m和n的具體關系，又知m和n分別是點A和B的橫坐標和縱坐標，則可以將點的坐標代入反比例函數解析式，從而分別獲得m和n與反比例函數k的關系式，即4m=k，－4n=k，消去k，恒等變形后即可得到m+n的值；（3）tan∠AOD+tan∠BOC=1，求直線AB的解析式，對于角的正切關系，需要將其放在具體的直角三角形中，先作AE⊥y軸，垂足為點E，再作BF⊥x軸，垂足為點F，如圖2，則則條件轉化為，其中，則，結合第（2）問m+n的值，解方程即可分別確定m和n，則A和B的坐標均可求得，利用兩點即可求直線AB的函數解析式.

圖1

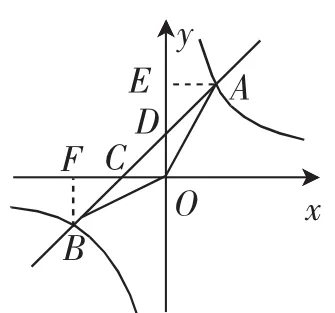
圖2

解：（1）當m=2時，得A（2，4），代入，可得k=8，則反比例函數解析式為，把點B（－4，n）代入，解得n=－2.

（2）點A和B均位于反比例函數曲線上，將其坐標A（m，4）和B（－4，n）分別代入解析式（k＞0），可得4m=k，－4n=k，即4m=－4n，整理得m+n=0.

（3）作AE⊥y軸，垂足為點E，再作BF⊥x軸，垂足為點F，在Rt△AEO中，tan，在Rt△BFO中，.因為tan∠AOD+tan∠BOC=1，則.又知m+n=0，解得m=2，n=－2，則點A和B的坐標分別為A（2，4）、B（－4，－2），則直線AB的斜率為1，利用點斜式，可得y－4=x－2，整理可得直線AB的函數解析式為y=x+2.

二、考題解讀及變式訓練

1.考題解讀

（1）考題的本質探索.

上述考題考查了兩種函數圖像，即反比例函數y=k x和一次函數y=kABx+b，以及三角函數，只不過將一次函數以兩點連線的形式給出，另外，問題中涉及了三角函數tanθ（θ代表不同的角）.分析反比例函數解析式及曲線上的點，需要認識其本質，對反比例函數解析式進行變形xy=k，由于k為常數，則曲線上的點必然滿足橫、縱坐標的乘積為一恒定的常數，即對于點A（x1，y1）、B（x2，y2）、C（x3，y3）、…，必然有x1y1=x2y2=x3y3=…=k，因此對于求反比例函數解析式或其上點的坐標，可以采用“（x1，y1）→確定解析式點（x2，y2）”的模式.而分析一次函數解析式離不開對點坐標的求解，由于解析式y=k′x+b中最多含有兩個未知數，因此其解析式的確定最多需要求得圖像上的兩個點.初中階段的三角函數都是放在直角三角形中來研究的，因此對于問題中的三角函數，需要在圖像中構建直角三角形，將其轉化為相關線段的比值，利用線段的長度比值來建立方程求解.對于含有多種曲線的函數題，其實質上就是對圖像的點、線、面之間關系的分析，最終還是需要結合函數解析式將其轉化為研究點坐標的問題.

（2）考題的難點分析.

上述題目涉及了三個問題，第（1）問是相對基礎的問題，只需借助“點坐標1→解析式→點坐標2”的模式即可完成.第（2）問求m+n的值，學生很容易陷入求解m和n的誤區，由于反比例函數的解析式不能確定，因此含有m和n的點坐標無法求得，解題的難點就在于建立關于m和n的參數關系，通過消去參數的方式來直接獲得m+n的值.本題目的一個特殊點在于點A的縱坐標與點B的橫坐標互為相反數，基于反比例函數k的幾何意義可得x1y1=x2y2=k，則必然有A的橫坐標與點B的縱坐標互為相反數，即m+n=0，該特點既體現在具體的數值上，也體現在圖像上，即A、B兩點關于原點O呈現中心對稱分布，這是該小問認識的難點所在.對于第（3）小問，其難點在于對含有三角函數條件的轉化，初中階段需要將其放在直角三角形中來研究，如何構建較為簡潔的直角三角形成為解題的關鍵.如上述解題過程分別作了點A和點B到y軸、x軸的垂線，構建了Rt△AEO和Rt△BFO，則很容易將其線段的比值與點的橫、縱坐標聯系起來，如若構建的直角三角形不合理，則相關線段長度就難以表示，會導致解題的失敗.因此在解題時不僅需要理解相關概念，還需要掌握相應的解題技巧，尤其是對于幾何題的輔助線添加需要細致斟酌，確保解題思維的順暢.

2.變式訓練

對于考題的第（2）問和第（3）問，可以進行相應的變式，在不改變問題主旨的前提下加深學生對知識的理解，進一步拓展學生的解題思維，現對問題進行如下變式：

變式：如圖3所示，反比例函數上存在A（m，4），B（－2，n）兩點，現經過點A、B作一直線，與x軸相交于點C，與y軸相交于點D，試再次分析相似問題：

（1）如果m=2，求n的具體值；

（2）試求2m+n的值；

（3）現連接OA、OB，設直線AB的解析式為y=k′x+b，如果tan∠AOD+tan∠BOC=1，請直接寫出不等式k′x+b≥的解集.

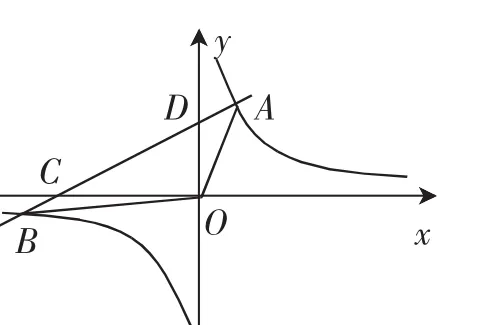
圖3

變式思考：第（1）問的解題模式依然不變，解得n=－4；第（2）問發生了變化，但基于反比例函數k的幾何意義獲得的關系式x1y1=x2y2=k，依然可以建立m和n的關系，4m=－2n，整理變形可得2m+n=0；第（3）問求不等式k′x+的解集，分析不等號兩邊，左邊為直線AB上點的縱坐標值yAB，右邊為反比例函數上點的縱坐標值y1，則問題轉化為x取何值時，yAB≥y1，圖像上的直觀體現則是直線AB的圖像位于反比例函數圖像的上方的x范圍.初步觀察可知為xB≤x＜0或x≥xA，則問題轉化為求點A和點B的橫坐標，銜接原考題求點A、B的坐標即可.

三、解后反思及教學思考

1.歸類圖像曲線，探尋考題本質

中考曲線壓軸題的考查類型是多樣的，涉及的函數圖像也較為眾多，如果僅僅將其看作多條曲線的簡單集合是不利于分析的，也無法獲得較好的解題策略.學習時需要對函數圖像進行系統歸類，對圖像本質進行深入探究，明晰曲線結構，理解函數解析式，掌握函數相關問題的求解方向，然后將多函數圖像進行歸類整合，從函數圖像的點、線、面之間的聯系入手，總結相應的解題方向和解題策略.教學中有必要將函數圖像設計成教學專題，引導學生對不同類型的圖像問題進行解法歸納，加深學生對圖像本質的理解，從而形成較為系統的解題策略.

2.注重分析方法，掌握解題思路

初中函數內容不僅需要掌握函數的解析式和圖像性質，還需要將兩者結合起來進行對應理解，這是函數內容的重難點，可以說函數是數學的代數知識和幾何知識的綜合.函數知識的綜合性同樣體現在函數問題的解題策略上，一般函數綜合題有圖像法、解析法，以及兩者結合使用的綜合法，如本題第（3）問的求解，從三角函數的性質來獲得解題的突破口，以及變式問題中求不等式的解集采用先分析圖像，后分析解析式的方式，均是對上述方法的充分使用，因此充分掌握函數綜合題的解法是十分必要的.在實際教學中需要結合考題向學生傳達該類題型的解法技巧，使學生深刻體會圖像法和解析法在解題中的應用思路.

3.透析表象問題，開展變式學習

函數圖像的綜合題雖然涉及的知識點多、問題形式多樣、圖像變化靈活，但實質上就是由基本的函數圖像進行的結合，其背后隱含的知識本質是不變的.初中階段常見的函數有一次函數、反比例函數和二次函數，因此只需要充分掌握上述函數的核心知識即可.另外，在教學中適時地對考題開展變式學習，對考題的問題進行適當改編，利用“形變質不變”的變式問題往往可以加深學生對考題本質的理解，如上述對考題的變式學習，揭露了函數綜合問題的核心就是點、線段之間聯系性的互化，問題的求解也需要基于此來完成.變式學習不僅是一種學習方式，還可以在求解變式問題中拓展學生的思維，使學生靈活思考，變通解題.

四、寫在最后

函數綜合題是初中階段的重、難點題型，雖然其綜合性強、復雜度高，對學生的解題思維有著較高的要求，但探尋其本質，同樣是眾多函數采用一定方式的結合，其中點的坐標是聯系各函數圖像的紐帶.求解時需要充分利用函數解析式，結合函數的相關性質，對問題和條件進行逐步轉化，必要時采用適當的解題模式來分析問題，探究解題的突破口.在對函數綜合題教學時，首先需要引導學生掌握函數的基本內容，理解函數的知識本質；然后在解題時向學生傳達科學的分析方法，使學生形成系統的解題策略，同時適時地開展變式學習，通過考題變式使學生透析問題實質，拓展學生的解題思維，真正掌握函數的知識精髓.

1.沈奕.深入研究揭示結構，歸類復習變式再練——以“曲線壓軸題”為例［J］.中學數學（下），2017（08）.

2.周紅梅.在教學中發展思維，在變式中提升能力——以2016年江蘇省泰州市中考第24題為例［J］.中學數學（下），2017（10）.

3.劉志波.活躍在反比例函數中的幾何圖形［J］.中學數學教學參考，2017（36）.

4.孫海鋒，趙韜.反比例函數、一次函數與二次函數綜合問題［J］.中學數學教學參考，2018（Z2）.H