一道二元變量求最值問題的解法賞析

☉江蘇省南京市第九中學 金玉明

一般地，對于一道二元變量求最值問題，常規(guī)解法往往都有幾種，如：配方法、消元法、不等式法、構(gòu)造法等，但是有些題目用這些常規(guī)解法卻難以求出最值，今天我們欣賞解一道這樣的題目所采用的幾種不同尋常的方法，感受一下學習數(shù)學帶給我們的樂趣.

題目已知正實數(shù)x，y滿足x2+y2=1，則的最小值為

本題若采用常規(guī)解法——消元法來解，由正實數(shù)x，y滿足x2+y2=1得，代入得，接下來讓人感覺無從下手，因為使用不等式或者用導(dǎo)數(shù)求最值的方法都不容易求出其最小值，但是可以使用下面幾種不同尋常的方法來解.

方法一：采用三角換元法

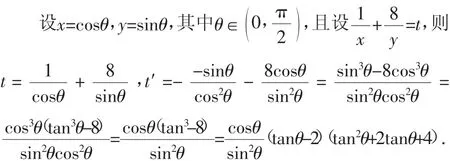
設(shè)），則當θ∈（0，θ0）時，t′＜0，函數(shù)在區(qū)間（0，θ0）上單調(diào)遞減；當時，t′＞0，函數(shù)t=在區(qū)間）上單調(diào)遞增.所以，當tanθ=2，即

說明：先采用三角換元，轉(zhuǎn)化為一個變量θ，再采用導(dǎo)數(shù)求最值的方法求最小值.

方法二：采用基本不等式公式推廣到3項時的公式

因為x2+y2=1，所以

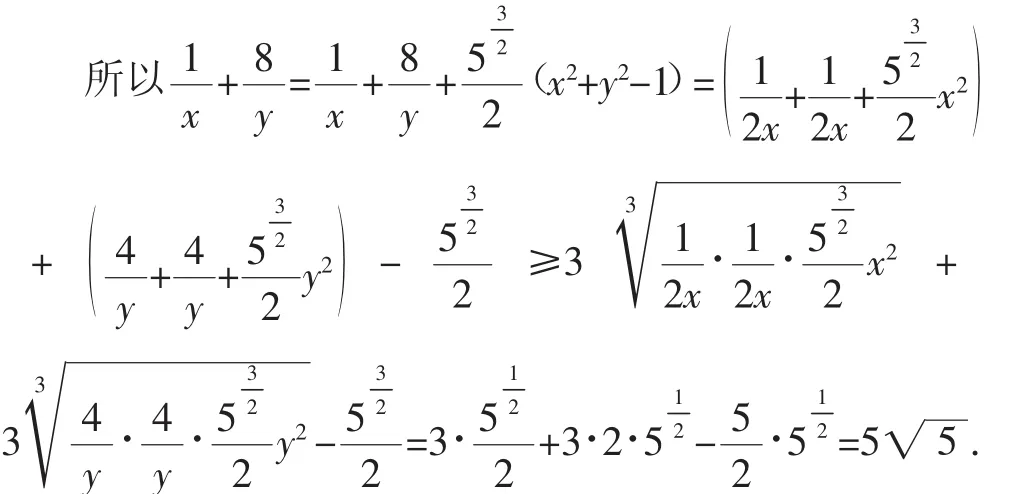
當且僅當時，取等號，所以

說明：基本不等式公式推廣到n項的公式為：若a1，a2，a3，…，an均是正數(shù)，則有均值不等式當且僅當a1=a2=a3=…=an時取等號.上述解法是運用推廣到3項時的公式.為了湊成3項乘積為定值，可以根據(jù)x2+y2=1，構(gòu)造λ（x2+y2－1）=0，λ∈R，然后將轉(zhuǎn)化為

方法三：運用常數(shù)轉(zhuǎn)變量的“1”的逆代

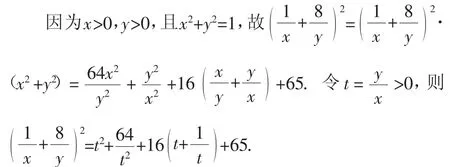
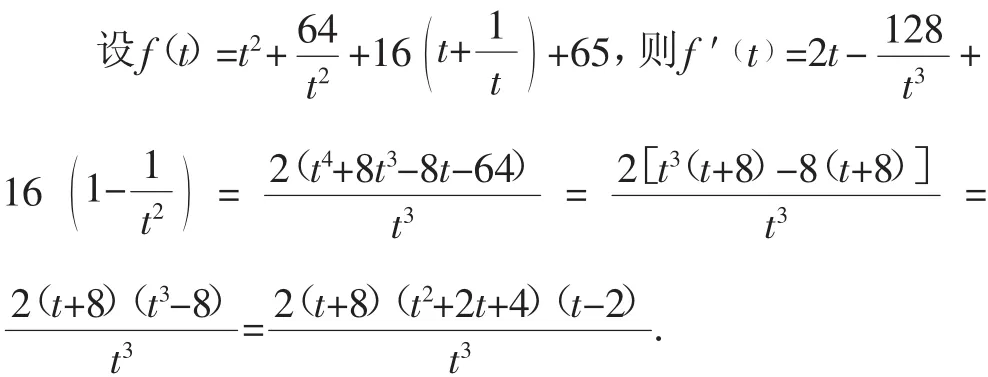
令f（′t）=0，得t=2，所以，當t∈（0，2）時，f（′t）＜0，函數(shù)在區(qū)間（0，2）上單調(diào)遞減；當t∈（2，+）時，f（′t）＞0，函數(shù)在區(qū)間（2，+∞）上單調(diào)遞增.所以，當t=2時，即取得最小值125，所以取得最小值

說明：根據(jù)x，y為正數(shù)，求的最小值可以轉(zhuǎn)化為的最小值，然后運用常數(shù)轉(zhuǎn)變量的“1”逆代的方法，將問題轉(zhuǎn)化為關(guān)于的函數(shù)，再采用換元的方法令，將問題又轉(zhuǎn)化為一元變量關(guān)于t的函數(shù)，最后利用導(dǎo)數(shù)求極值的方法求出的最小值.

方法四：利用權(quán)方和不等式公式

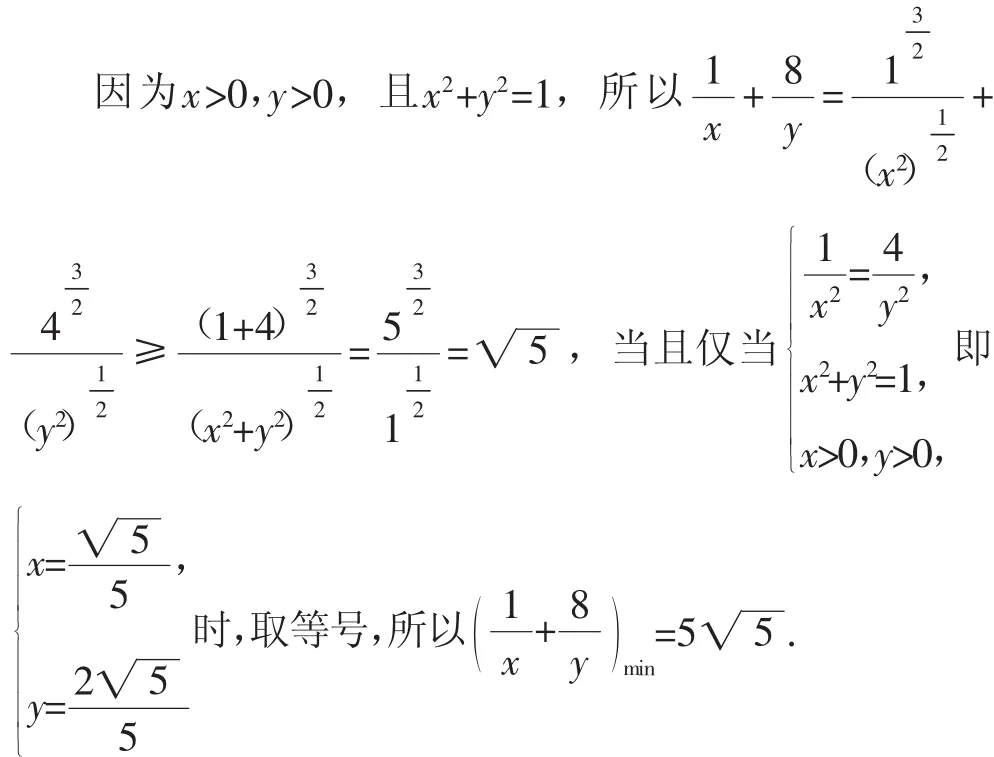
說明：權(quán)方和不等式公式為：若 ai＞0，bi＞0，m＞0，則成立，當且僅當時，等號成立，m稱為該不等式的權(quán)，該不等式的特點是分子的冪指數(shù)比分母的冪指數(shù)高1.根據(jù)此不等式，只要湊成該公式的適用形式，就可以利用此公式迅速解題，非常方便實用.

對于這道題目，常規(guī)解法配方法、消元法、基本不等式法、構(gòu)造法等都很難求出其最小值，但是我們可以綜合運用三角換元法，導(dǎo)數(shù)求極值法，基本不等式的推廣公式，以及權(quán)方和不等式等使問題得到圓滿解決，看似到了山重水復(fù)疑無路的絕境，其實藏有柳暗花明又一村的美景，等待我們?nèi)グl(fā)現(xiàn)，去欣賞，只要我們不斷學習，努力探索，就會在數(shù)學的知識海洋里暢游，流連忘返，樂此不彼.H