為論題活動的有趣互動喝彩*
——一道原創向量題的論題比賽實錄與思考

☉浙江省鄞州中學 楊 潔

☉浙江省寧波市教育局教研室 任偉芳

作為教研活動的一種創新嘗試，寧波市教育局教研室近日舉行了以“學科核心素養背景下的新高考研討活動”為主題的原創題目論題比賽.相對于由一個人展示的說題比賽活動，論題需要兩位或兩位以上教師共同展示，是說題的升級版，形式新穎，對教師綜合素質要求高.比賽要求參賽教師結合近年浙江高考的命題特點自主命題，并在命題的基礎上選取一道有意義的原創試題在現場對題目進行有情景的論題展示.每組團隊須在15分鐘內完成論題展示.經過層層選撥，最后有七個隊進入決賽，在決賽現場選手們的論題展示形式豐富多彩，主要有論壇答辯、師生角色答疑、教研沙龍等形式，精彩紛呈的論題情境引起了參會一線教師的濃厚興趣和陣陣掌聲.筆者所在的組在比賽中別出心裁地以論壇答辯的模式，對一道原創平面向量題進行“編—辯—變”，得到了評委和與會教師的一致好評，最終獲得了一等獎中的第一名.下面是本組論題的實錄和比賽后的思考，愿與大家分享.

一、論題比賽現場實錄

本組參賽選手一共由四位教師組成，展示中所扮演的角色分別是：①論壇主持人：對論壇節目進行介紹，調節現場論題氛圍，促進嘉賓之間的交流和內容的總結，由筆者擔任；②特約嘉賓一：命題專家兼教師，主要從命題角度分析題意和考查目標；③特約嘉賓二：一線任課教師，主要分析題目的解法和試題的教學價值；④特約嘉賓三：高三學生代表，代表多數學生提出對試題的質疑和做題時遇到的障礙，由老師扮演，問題來自該位老師所教班級學生做了這道題目后提出問題的大數據分析收集.

（一）“編”考題

首先，主持人向與會老師介紹了“論壇”的參賽形式，并言辭幽默地對臺上角色進行介紹，調節氣氛，進入主題.

主持人：尊敬的各位老師大家下午好，本組論題比賽將以“論壇辯題”的形式，以“編—辯—變”為主線展開.今天迎來了三位嘉賓：一號嘉賓，命題專家兼教師董老師，高端大氣上檔次；二號嘉賓，一線任課教師賴老師，低調奢華有內涵；三號嘉賓，高三學生代表陳同學，賣萌嘟嘴剪刀手.

主持人：三位嘉賓，你們好！（相互握手）歡迎來到論題特約論壇，此次嘉賓給大家帶來的是一道原創的平面向量題.

題目 已知向量a，b，滿足a·b=0，且|a-b|=|a-2c|=2，則a·c的范圍是______.

主持人：請問此試題適合考查的對象是高幾學生？

嘉賓1：試題適合浙江高三學生考評，學生已完成一輪復習，知識體系已經完整，切入點相對多.嘉賓2：嗯，是的，不過作為向量壓軸小題，易丟分，對多數學生來說還是很有難度的.

主持人：縱觀浙江高考平面向量客觀題的命題特點，穩定中凸顯變化，變化中追求創新，那么請問兩位嘉賓，此命題的命題特色和考查目標是什么？

嘉賓1：請看題，此題符合浙江高考命題特點——簡潔、清晰、明了.

主持人：嗯，確實是.本題的三維目標是什么？

嘉賓1：知識與技能：掌握向量運算的幾何意義，平面向量的坐標運算，向量的綜合應用等內容；過程與方法：學生在自主探究的過程中，感受數形結合和等價轉化思想，提高分析問題和解決問題的能力；情感態度與價值觀：學生在方法相互探討中，經歷成功的體驗，激發學習興趣和探究欲，拓展思維的深刻性和廣闊性.

主持人：本題有哪些命題特色？

嘉賓1：（1）關注基礎落實.本題在解法中涵蓋了向量的線性運算，平面向量的向量數量積的代數、幾何意義.題目取材于人教版教材必修4第109頁的例1，是對課本例題的深入挖掘.命題追求解法多，入口寬，對學生基礎能力提出了一定的要求，為高三向量復習指明了方向.（2）關注能力提升.波利亞認為，中學數學教育的根本目的是教會學生思考，向量問題之所以難，在于學生在解題思路形成過程中產生了困惑.而本題的四種解法的教學能對向量解題起到舉一反三作用，為學生形成思路、跳出茫茫題海鋪平了道路.（3）關注核心素養.本題著重考查了學生邏輯推理、數學建模、數學運算、直觀想象等數學核心素養.

（二）“辯”思路

此環節主持人在論題過程中對題目本身提出種種疑問并及時總結，三位嘉賓在論思路過程中重構了不同層次學生的解題思路與解題障礙，通過相互質疑，突出探究過程，碰撞出思維的火花.這里為體現論的過程，特選取主要對話如下.

主持人：各位專家教師和學生代表，能跟大家分享下學生的答題情況嗎？

嘉賓2：（思路1）從學生做題情況來看，學生主要會從向量運算的幾何意義去考慮問題：

令a，b，c向量公共起點O，由向量垂直和向量減法運算的幾何意義可知，O在以AB為直徑的小圓上運動，2c的終點C2在以A為圓心，2為半徑的大圓上運動.

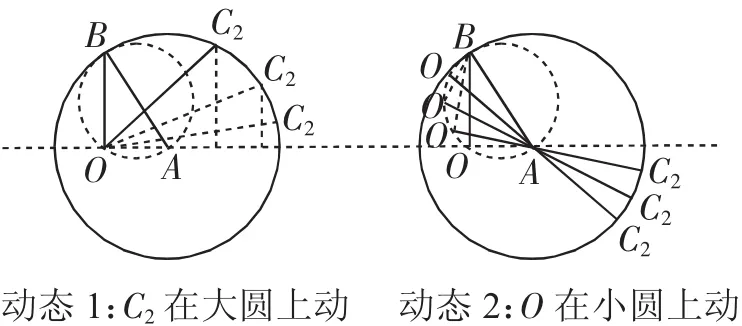
圖1

先讓C2在半徑為2的大圓上動，發現當—同向時，取到最大值；再讓O在半徑為1的小圓上動（如圖2），發現當O運動到B時取到最大值為取到最小值時，必定有反向.又因為|=2，由基本不等式知，當且僅當O在的中點時，

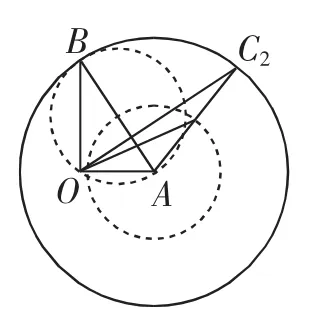
圖2

主持人：感謝這位嘉賓，剛從運動觀點和幾何變化角度進行分享，能培養學生的數學直觀想象素養.那么這位學生嘉賓，請問你有什么疑問嗎？

嘉賓3：（思路2）由垂直關系自然嘗試建系、設點.如圖3所示，以O為坐標原點建系

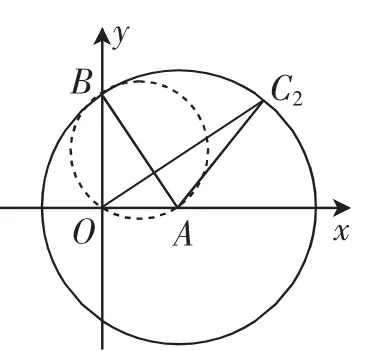
圖3

設A（a，0），B（0，b），C2（a+2cosθ，2sinθ），

因為a2+b2=4，

所以a∈［-2，2］，cosθ∈［-1，1］.

那么，數量積問題轉化為求關于a，cosθ的二元函數最值問題，之后就會遇到困難……

經過討論，然后如下解決了（學生代表表現靈光一現狀）

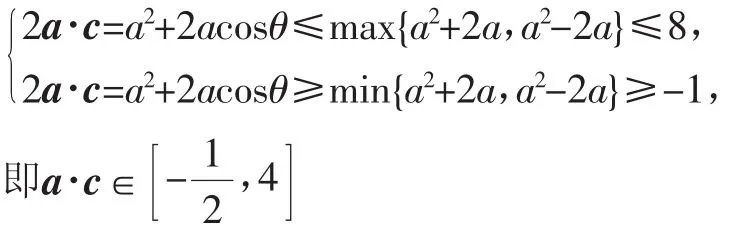
嘉賓1：（思路3）不錯，這位學生嘉賓，看到這個函數還可以脫離圖形，直接利用已知向量形式對目標進行轉化，從而問題轉化為求二元函數最值問題.

2a·c=［a-（a-2c）］·a=|a|2-2|a|cosθ，θ表示a-2c與a的夾角，下同上.

主持人：真好，向量不愧是集幾何形式和代數形式于一身，不僅能從幾何角度去思考，還能很好地用代數方法解決，這里綜合考查了學生的化歸能力和數學運算素養.

嘉賓2：（思路4）等等，主持人，說起代數角度，學生最容易做的嘗試應該是對等式兩邊進行平方.|a-2c|2=|a|2+4|c|2-4|a||c|cosφ=4.

嘉賓3：是呀，但是平方后處理不下去了……（賣萌，苦思冥想狀）

嘉賓2：考慮到|a|∈［0，2］，故嘗試以|a|為主元進行配方，再想辦法得到a·c的范圍，如下.|a-2c|2=（|a|-2|c|cosφ）2+（2|c|sinφ）2=4，得-2≤|a|-2|c|cosφ≤2，兩邊同乘|a|可得，-2|a|≤|a|2-2a·c≤2|a|. 整理后，2a·c≥|a|2-2|a|≥

主持人：是的，兩邊平方法在各類向量題中也經常出現，具有較廣的教學意義，平方后的處理因題而異，能對不同層次的學生思維進行提升和拓展.

（三）“變”推廣

此環節中一位嘉賓提出變式，其他嘉賓質疑變式來源以及變式的教學意義.

推廣1：從題目本身角度進行變式.下面變式分別從改變題目中的條件（系數或夾角），改變所求的目標，條件與結論互換角度進行了題目的變式.

變式1：已知向量a，b，滿足a·b=0，且|a-b|=|a-4c|=2，則a·c的范圍是______.

變式2：已知向量的a，b，夾角為60°，且|a-b|=|a-2c|=2，則a·c的范圍是______.

變式3：已知向量a，b，滿足a·b=0，且|a-b|=|a-2c|=2，則b·c的范圍是______.

變式4：已知a，b，滿足a·b=0，且|a-b|=|a-2c|=k，若a·c∈［-2，6］恒成立，則k的范圍是______.

推廣2：從解法模型角度進行研究：

本題在解法中體現了二元函數最值問題的求法，這在近年高考與模擬題中也有所體現.

可以發現，近年來與此相關的試題有很多，其具有很廣的教學價值，教師在教學中可以加以滲透.在此環節中現場PPT展示了若干相類似的高考真題和模擬題.

回顧現場，參賽教師整個過程語言幽默，輕松愉快，邏輯清晰，重點突出，精彩地完成了論題過程，贏得與會老師的陣陣掌聲.

二、對論題比賽價值的思考

相對于說題，論題比賽不僅在形式上更加新穎活潑，在內容上所強調的點也有所不同.筆者結合此次論題比賽的親身經歷，對論題活動的價值進行以下思考.

（一）論題有說題優點并且有趣、有情境

論題與說題類似，教師在論題前也需要進行的一系列準備工作，如查閱資料、理論學習、考試題研究等，這都有利于提高教師命題、解題水平，有利于提升教師的教研水平.在現場論題展示活動中，教師同樣展示了自身教育理論功底、學科知識掌握程度、解題方法理解能力、對教學前瞻性理念的探求.論題是說題的升級版，是一種新的教研模式嘗試，由多位教師合作參與，即重視多種不同解法的闡述，同時突出不同角度思維的探究過程，不但能在豐富有趣的情境中提升教師專業水平，論題中不同角色的扮演還能促進在課堂中自然順暢地落實核心素養.

（二）論題凸顯了探究過程有利于思維在碰撞中升華

相對于說題只需要由一人講座，論題比賽的現場需要由多人一起展示.問題的切入點不同必然呈現出不同的解題思路，論題中不僅要像說題那樣說出各種解題方法，還需要在多人互動合作中道明各種方法的來源和探究的過程.以本組現場論題比賽展示的第二個環節“論思路”為例，不同嘉賓之間的相互提問和相互補充過程不僅清晰地道出了題目的題意、目標、一題多解，更重要的是重構了不同解題思路的來源和解題障礙.論的過程即是探究過程的再現，非常有利于理順解題的思路來源，深層次揭示求解數學題的思維過程和題后的隱形問題，突出數學本質，有利于思維在交流碰撞中產生火花.

（三）論題引導教師換位思考，提高試題教學價值

論題現場中的不同角色，命題者或教師或學生等，對話中能生動清晰地反映不同角度的思考過程，暴露對題目的不同理解，給與會教師一種身臨其境，真正走入題中的真實感.參賽教師要做好角色轉變，在論題前需要深入了解所扮演的角色的思維習慣和思考方向.以文中論壇出現的角色——三位嘉賓（命題專家、專業教師、學生代表）為例，賽前幾位教師做了如下工作：嘉賓之命題專家需要研讀考綱，針對高考中平面向量的高頻考點命制試題，明確命題目標、命題意圖；嘉賓之專業教師需要根據學情對教學過程進行設計，研究試題的變式和教學價值；嘉賓之學生代表需要融入學生之中，了解學生的各種解題方向以及每個方向中可能出現的不同障礙，分析錯解形成的原因等.當然，這幾方面的準備由整組幾位參賽教師合作參與.對于論題者，參賽教師不僅提高了自身對數學知識的熟練程度，還引導其在備課中換位思考，多角度分析，加強了對學情及最新高考命題動態和趨勢的洞察力.對于聽者，在生動的對話展示中不易產生聽覺疲憊，能更容易抓住題目的核心價值，得到理論滋養和案例示范兩方面的收益.最后結合評題教師的專業反饋，集體的智慧得以充分發揮，達到取長補短、優勢互補的效果.

（四）論題能研討課堂預設，促進教學互動

年輕教師在教學中容易發生教學條理不清晰，教學內容的數學本質挖掘不深刻，內容和內容之間的聯系剖析不透徹，教學重點抓不準，教學節奏控制不住，課堂中的即時教學機會抓不住，教學引導不到位而造成的教學超時或教學縮水等情況.筆者認為，這是由于教師在備課過程中缺少課堂預設造成的，這預設中包括對不同學生解題方法、思維障礙的預設，缺少這方面的預設，課堂中就容易出現學生理解不是很透徹，或講了但選擇的方法不夠自然，導致學生不易掌握的現象.在此次論題展示中，嘉賓學生代表的語言和肢體動作的表現，如苦思冥想狀，赤裸裸地將學生可能出現的最大解題障礙暴露出來，引起了大家對問題的關注.經常參與這樣生動的論題，教師必然更容易發現學生的思維障礙，設身處地地去從學生的角度思考問題.在課堂教學中，教師也就能更好地實現與學生的思維碰撞，產生有效的互動，鼓勵學生敢于對問題加以探索和創新，激發學生潛能，最終促進學生對知識本質的理解.

總之，本次在創新命題基礎上舉行的論題活動的嘗試給教師教研活動帶來了一個全新的視角，有利于教師專業化素養發展.通過創新命題，選取有價值的題目，以論題的形式予以互動和交流，這樣既提高了教師對有價值試題的探究能力，使得命題水平得到進一步的提升，也大大提高了教師在課堂教學中對學生思維能力培育，使得教學更加有效.論題為學科的教研活動提供了一種實用有效的創新模式，可以在備課組、教研組、區市這幾個層面開展論題教研活動，精彩的論題比賽定會獲得更多一線老師的喝彩.