一道不等式組例題的變式探究

☉湖北省武漢經濟技術開發區武漢外國語學校 胡春洪

一、原題呈現

人教版七年級數學下冊第9.3節一元一次不等式組有這樣一道例題：當x取哪些整數值時，不等式5x+2＞3（x-1）與x-1≤7-x都成立？

二、變式探究

下面我們引入“參數”，從特殊到一般，對原例題進行“變式”，將一些常見的含參不等式組整數解問題“串聯”起來.變式1：若關于x的不等式5x-a＞3（x-1）與x-1≤7-x的解集中，相同的整數解恰好是7個，求a的取值范圍.

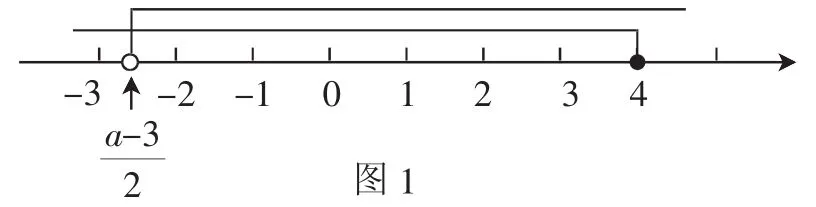
圖1

評注：變式1其實就是將原例題中不等式5x+2＞3（x-1）中的“2”換成-a，并將例題的結論“7個整數解”作為條件，求a的取值范圍.借助原例題，可以部分地“驗證”一下a的取值范圍是否求對了.當-a=2，即a=-2時，兩不等式相同的整數解恰是7個顯然成立.而事實上，a=-2也確實在-3≤a＜-1的范圍內，所以可以初步判斷所求取值范圍的合理性.教學中引導學生驗證，既是讓學生感受特殊與一般的辯證關系，同時也是在潛移默化中培養學生的“數感”.

圖2

評注：變式2比變式1更進一步，兩個不等式都含參數m，從而不等式組的解集是用含m的式子表示的，乍一看似乎無從下手.解決問題的關鍵是發現必有整數解0，進而確定其他6個整數解，從而將問題歸結為變式1的情形.需要注意的是“臨界狀態”，-m不能取-3，否則2m=6，原不等式組解集為-3＜x≤6，共有9個整數解；2m不能取4，否則-m=-2，原不等式組解集為-2＜x≤4，共有6個整數解.

解析：由變式2可知，原不等式組恰好有7個整數解時，2＜m＜.所以當原不等式組至少有7個整數解時，m＞2.故m的最小整數值是3.

評注：借助數軸分析可知，原不等式組至少有7個整數解，則至少包含-2，-1，0，1，2，3，4這7個整數解，所以解得m＞2.同樣注意這里2m不能等于4，否則解集為-2＜x≤4，共有6個整數解.

分別令m=1，2，3，…，2m=1，2，3，…，分段討論可得原不等式組的整數解與m的取值范圍的對應情況如表1.

由表1可知，原不等式組至少有7個整數解時，m＞2.還可以看出，原不等式組有解，且至多有7個整數解時，m的取值范圍是0＜m＜2.5.

因為原不等式組的整數解的和是7，而3+4=7，-2+（-1）+0+1+2+3+4=7，所以，整數解是3，4或-2，-1，0，1，2，3，4.

綜上所述，a的取值范圍是7≤a＜9或-3≤a＜-1.

評注：變式4條件是整數解的和是7，而最大的整數解是4，很容易只想到整數解為3和4，而漏掉另一情形.所以碰到“和”的條件時，需考慮是否有正負抵消的情形.深層次反思一下，是因為本題中4-的值不確定，所以不含左端點，長為4-的線段蓋住的整數點的個數不確定，并且將7寫成連續整數的和的形式不唯一，從而出現分類.

表1

評注：比較變式5與變式4，變式5的解集兩端都含參數a，因此無法象變式4那樣可以確定最大整數解，但巧妙的是，變式5中隱含兩端的距離是2，從而不需像變式4那樣要分兩類討論.若將不等式組中第二個不等式中的等號去掉，即不等式組改為則相當于長度為2，不含左、右端點的線段蓋住整點的問題.而此時可以蓋住1個整點，也可以蓋住兩個整點，即整數解可能是3，4，也可能只有7，從而6，解得7＜a＜9或a=15.

如圖3，當相同的整數解是3，4時，2＜m-2≤3，解得4＜m≤5；

圖3

如圖4，當相同的整數解是-2，-1時，-1＜m+2≤0，解得-3＜m≤-2.

故m的取值范圍是4＜m≤5或-3＜m≤-2.

圖4

三、感悟反思

綜觀變式1到變式6，可以看出，解決含參不等式組的整數解問題，很關鍵的一步是確定整數解是什么，再據此列式確定取值范圍.一般步驟為：解不等式組→定整數解→數軸表示→列式求解.列式時需注意臨界狀態，從而決定不等式是否帶等號.

課本上的例、習題，雖然難度不大，卻有很強的“再生”功能.在日常的課堂教學中，教師引導學生對課本典型的例、習題進行變式研究，挖掘題目的廣度和深度，往往能起到事半功倍的教學效果，能讓學生跳出題海，避開重復無效的訓練.目前在課堂變式教學中，對幾何圖形進行變式研究的居多，而對代數問題進行變式研究的少.其實，代數問題一般化，引入參數，即可實現變靜態問題為動態問題.在解決問題時往往需要分類討論，數形結合，轉化化歸等.

通過一題多變，不僅使涉及的知識與方法處在動態的發展過程中，而且學生的思維活動將在不同的方向和層次上展開.學生可以體會由特殊到一般的探究方法，感受由靜到動，由淺入深，螺旋式上升的變化過程.在分析、比較、化歸、探究的過程中激活和綻放思維，有效提升解決問題的能力，與此同時數學素養也在探究中潛滋暗長.