察其形 思其源 謀其法
—— 對一道幾何最值問題解法的思考

☉浙江省三門縣三門初級中學 丁堅鋒

一、緣起

2018年5月5日晚上，一位朋友發來一道數學題（見“原題呈現”）要我幫忙解決，我便畫了一個圖發給他，如圖2，并在圖下方寫了“當O、E、C共線時，OC最大”.我本以為就此完事，不料，為把解法中的“理”說通，竟花去了1個小時.現將部分對話記錄如下：

朋友：為什么這個位置最大？怎樣證明這三點共線時，OC就最大？

朋友：E換成點D不也有這種關系嗎？為什么就要取中點E?

筆者：因為AB在滑動時，OE是定值，OD是在變的.

朋友：這個我懂，但解釋不了為什么E與O、C共線時，OC最大.

筆者：關鍵有兩點：（1）找到運動中的不變量；（2）提取數學模型.

朋友：你的解釋很抽象啊！我就覺得，用你的理由解決這個問題不夠嚴謹.沒有哪個定理或結論能直接用來解釋這個的吧？

筆者：我猜你的困惑在于為什么選擇OE而不選擇OD去解決？

朋友：我就是這個問題，怎么解釋當E在OC上時就達到最大，不要說OE是定值.

筆者：選擇點E還是選擇D與定理無關，這是一個解題策略問題，就好比選參照物.為什么不選D點，是因為OD在變，選擇這個變量對解題無用，所以我不選.那么，為什么選OE就可以呢，一方面它是定值，恰好CE也是定值（三個量中有兩個定值），另一方面OE、CE、OC剛好在一個三角形中，所以這個方法有可行性，然后找理論依據去證明.

朋友：懂了，還是策略問題，這是初中對付這種動態問題的一種策略.

我的這位朋友原先在初中教書，我本以為添幾條輔助線，畫個圖就可以了，沒想到的是他不上講臺講課了，把初中的一些知識和解題經驗忘得差不多了.朋友的困惑在于為什么是AB的中點而不是其他的點與O、C共線時求得最大值.我驟然想起，我們的學生是否也會有類似的困惑，隨即反思教學中是否存在這樣的一些現象：（1）講題時憑教師自己的認知水平和解題經驗講，與學生的認知和經驗不能平等對接，出現學生似懂非懂、不懂裝懂的現象；（2）沒有講清楚這個問題中選擇點E的合理性，這類問題選中點解決是否都可行；（3）沒有講清楚問題的本質特征、類似問題的區別，沒有著眼于通性通法，導致學生出現方法的負遷移.這些現象正是導致學生“做過的題會做，沒做過的題不會做”的根本原因.

二、思問題解決之源

原題呈現 如圖1，射線OM⊥ON，△ABC中，AB=AC=10，CD⊥AB于D，且CD=8，若△ABC的頂點A與B各自在射線OM、ON上滑動（△ABC的形狀、大小不變），則點C到O的距離最大值為（ ）.

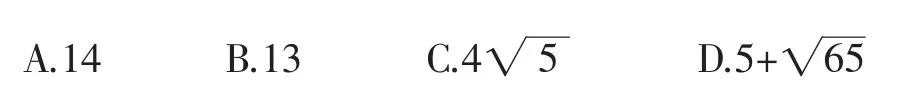
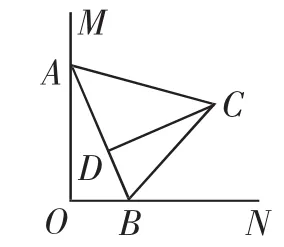
圖1

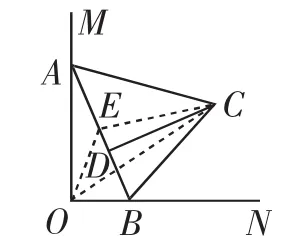
圖2

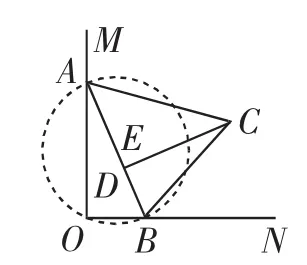
圖3

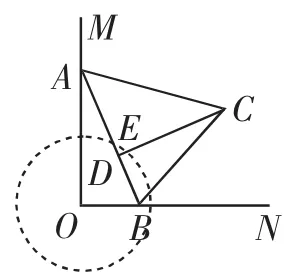
圖4

分析：取AB的中點E，因為∠AOB=90°，AB=10，所以OE=5，因為AC=10，CD⊥AB于D，CD=8，所以AD=6，BD=4，DE=1，所以CE=，結合OE、CE、OC所構成的三角形的三邊關系，可得OC的最大值=OE+CE=5+

這個解法的關鍵是抓住了運動中的不變量OE、CE，當AB在運動時，OE、CE、OC這三者處于同一個三角形中，且存在一定的數量關系，通過研究它們的位置關系和數量關系求出最大值.

那么，為什么就要找AB的中點呢？尤其對于解題經驗不豐富的學生來說，會不會顯得有點突兀？任何解法的產生都有它的緣由，而不是憑空出現的，有的是因為經驗使然，有的是經過探索偶然發現的.解題的途徑可能有多種，但是，解題過程中所經歷的思考過程可能是相似的，波利亞在《怎樣解題》一書中指出，解題時要充分分析已知條件，擬定計劃，實施計劃，最后找到解題的思路.他的解題四步驟具有普適性，我們可以參照他的方法進行思路起源的分析.

事實上，我們通過分析已知條件，從不同的角度可以得到一些有價值的結論：（1）△AOB是直角三角形，所以去聯系直角三角形相關的性質（斜邊中線性質），當AB在滑動時，OE的大小不變，如圖2；（2）注意到∠AOB=90°，所以想到以AB為直徑的圓，當AB在滑動時，這個圓的大小不變，如圖3；（3）由OE的大小不變，想到E的運動軌跡是一個圓，如圖4.從解題經驗來看：（1）中點往往是解題的關鍵點，尤其當遇到直角三角形或等腰三角形時，自然地聯想到與中點相關的定理；（2）兩點間的距離最小值問題有關的數學模型有“兩點間線段最短”、“垂線段最短”、“曲柄連桿模型”等.然后，通過把從已知分析得到的結論與經驗積累的解題策略相聯系，逐步消除與目標問題的差距，就能找到解題的途經.圖2、圖3、圖4中的方法都可以歸納為利用“曲柄連桿模型”進行解釋.“曲柄連桿模型”如圖5～7，圖5為曲柄連桿實物圖.如圖6，當N位于OM上時，OM最大；如圖7，當O位于MN上時，OM最小.這個模型的特征是“曲柄”中的兩條線段ON和MN是定長的，其中ON繞點O旋轉.

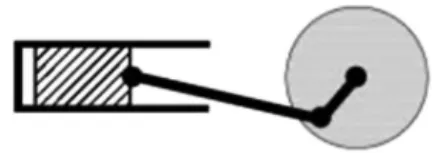
圖5

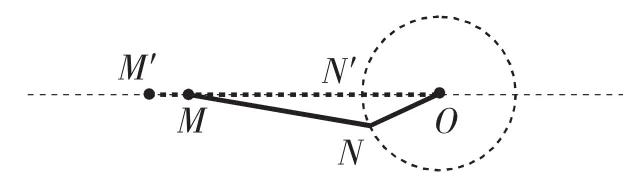
圖6

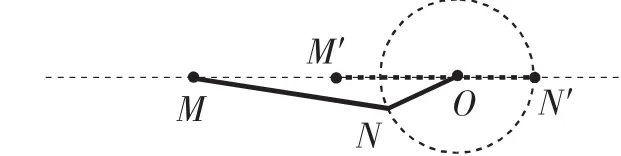
圖7

所以，選擇AB的中點去解決這個問題是基于圖形本身的特征和性質，結合相關數學模型，經過嘗試性探究后，得到的一種可行的方法.那么，這是一種通法嗎？對于這類題來說，不是.

三、謀解決問題之法

筆者初步了解，這類題在中考中最早出現在2012年濟南市中考數學試題中，如例1，以后各地對此問題進行變式，如例2、例3.例2與例1在條件結構上極其相似，解法上具有通性（找AB的中點），學生利用例1獲得的解題經驗便能很快地解決；倘若例3中仍找AB的中點可能就解釋不通了，盡管當OC最大時，O、E（AB的中點）、C共線，但是其原理與例1是不一樣的.

例1 如圖8，∠MON=90°，矩形ABCD的頂點A、B分別在邊OM、ON上，當B在邊ON上運動時，A隨之在邊OM上運動，矩形ABCD的形狀保持不變，其中AB=2，BC=1，運動過程中，點D到點O的最大距離為（ ）.

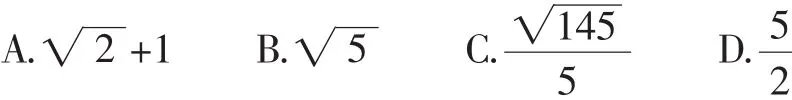
解：略.

圖8

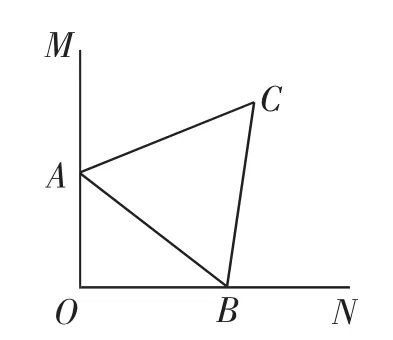
圖9

例2 如圖9，∠MON=90°，邊長為2的等邊三角形ABC的頂點A、B分別在邊OM、ON上，當B在邊ON上運動時，A隨之在邊OM上運動，等邊三角形的形狀保持不變，運動過程中，點C到點O的最大距離為（ ）.

解：此略.

例3 如圖10，在直角坐標系xOy中，已知正三角形ABC的邊長為2，點A從點O開始沿著x軸的正方向移動，點B在∠xOy的平分線上移動，則點C到原點的最大距離是（ ）.

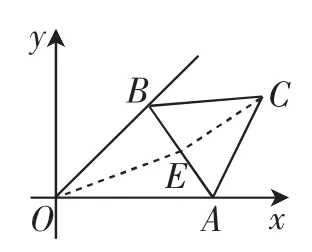
圖10

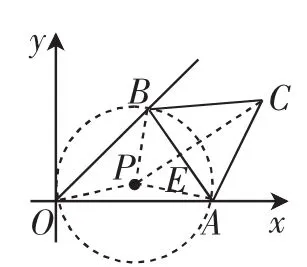
圖11

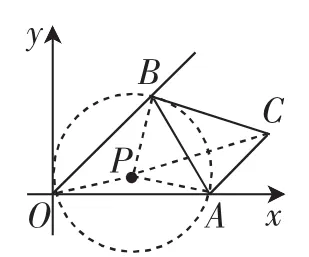
圖12

分析：如圖10，若取AB的中點E，當AB在滑動時，OE的長度在變，OC≤OE+CE=OE+，只有當OE最大時，OC才能達到最大，但當E落在OC上時，從幾何直觀上看并不能確定此時的OE就是最大的.對比“曲柄連桿模型”的特征，我們應先找到“曲柄”中哪一條柄在旋轉，即找出這個定圓，聯系相關點O、A、B，確定△ABO的外接圓，如圖11，P是圓心，因為∠APB=2∠AOB=90°，所以OP=PB=PA=，PC=1+，所以當AB在滑動時，圓P位置改變，大小不變，OP、PC就是“曲柄”中的兩條“柄”，問題便可解決.

解決這類題的關鍵是找到“曲柄連桿模型”中的兩條“柄”.進一步變式，如圖12，將例3中的△ABC改為普通三角形，其分析的原理是一樣的.我們注意到，當OC最大時，OC并不經過AB的中點.

那么，為什么例1例2中當O、E（AB的中點）、C共線時能得到OC最大值呢？這是因為∠AOB=90°，△ABO的外接圓圓心恰好是點E，這是一個特例.所以，僅僅告訴學生取中點，并沒有從問題根源來思考，容易被學生誤解成只要取中點就能解決問題，導致方法的負遷移.在教學中，應該抓住問題的本質，先進行一般性方法的探究，掌握通性通法后，再去關注特例，這樣有利于學生良好思維的養成，解決問題能力的培養.

四、反思

中點往往是一類問題解決的突破口，利用中點有關的性質去探尋解決問題思路是值得嘗試的方法，但是，利用中點不是生硬的套用，而是從圖形特征出發，充分分析已知條件后自然產生的知識應用.如在上述問題中，取AB的中點僅在特殊情況下可行，但并不是解決這類問題的通法.教學中，要把隱含在特例背后的依據講清楚，才不會使學生產生錯覺，才能知一題會一類.

數學解題能力的養成離不開經驗的積累，經驗中既有學習方法方面的，也有解題技巧方面的，教學中不能過分強調技巧，否則會固化學生思維，被經驗所左右，在遇到新問題時，可能會因為“技”不對題，想不到技巧而一籌莫展.在解題教學中，使學生逐步養成從基本概念、基本原理及其聯系出發思考和解決問題的習慣，這是發展學生思維的正道.所以，教會學生分析問題，重視解決問題的通法才是培養能力之根本.