細品讀 善聯想 巧破解
——對一類“定義特殊四邊形”求邊長的試題探析

☉浙江省紹興市柯橋區平水鎮中學 沈岳夫

眾所周知，四邊形是初中數學中的重要內容，而教材中主要研究的特殊四邊形有平行四邊形、矩形、菱形、正方形.為了體現試題的公平性，也為了提高試題的效度和區分度，命題者巧妙地采用新定義特殊四邊形的形式呈現，而這類試題往往是以“給出定義→探究性質→實際應用”的形式呈現，要求學生內化約定的幾何定義，提取關鍵信息，利用定義的核心探究幾何的性質，最后應用性質實現問題的解答.本文特遴選3道有關“定義特殊四邊形”求邊長的中考試題，供大家賞析.

一、從邊、角的視角定義特殊四邊形

例1（2017年浙江·紹興卷）定義：有一組鄰邊相等，并且它們的夾角是直角的凸四邊形叫作等腰直角四邊形.

（1）如圖1，等腰直角四邊形ABCD，AB=BC，∠ABC=90°.

①若AB=CD=1，AB∥CD，求對角線BD的長；

②若AC⊥BD，求證：AD=CD.

（2）如圖2，在矩形ABCD中，AB=5，BC=9，點P是對角線BD上一點，且BP=2PD，過點P作直線分別交邊AD、BC于點E、F，使四邊形ABFE是等腰直角四邊形，求AE的長.

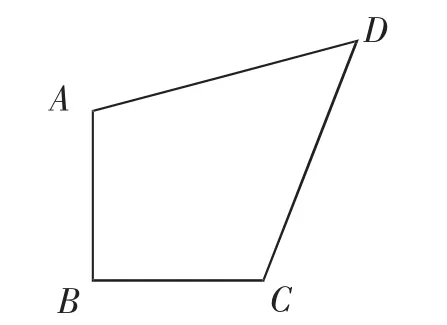
圖1

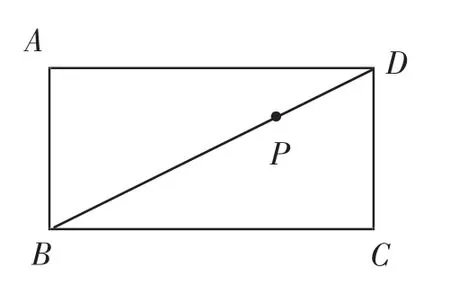
圖2

思路剖析：（1）①根據題意，只要證明四邊形ABCD是正方形，即可求得BD=.

②連接AC、BD，只要證明△ABD≌△CBD，那么AD=CD成立.

（2）若EF⊥BC，則AE≠EF，BF≠EF，四邊形ABFE不是等腰直角四邊形，不符合條件.

若EF與BC不垂直，

①當AE=AB時，如圖3，此時四邊形ABFE是等腰直角四邊形，則AE=AB=5.

②當BF=AB時，如圖4，此時四邊形ABFE是等腰直角四邊形，則BF=AB=5.因為DE∥BF，可得DE∶BF=PD∶PB=1∶2，解得DE=2.5，所以AE=6.5.

綜上所述，滿足條件的AE的長為5或6.5.

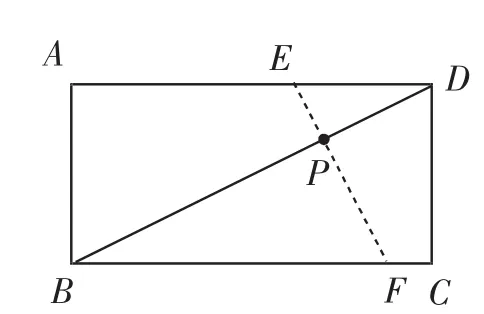
圖3

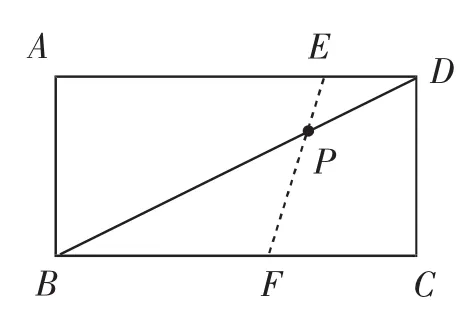
圖4

評注：此題從鄰邊及夾角的視角定義了“等腰直角四邊形”，并引導學生經歷“認識概念—研究性質—分類探析”數學探究性學習過程.此題考查學生將相似三角形的判定和性質與其他知識綜合在一起解決問題的能力.第（1）問簡單易入手.第（2）問梯度明顯增大，需要學生真正理解、內化“等腰直角四邊形”的定義，由于EF是經過點P的動直線，因此需要分類討論、縝密思考，這正是命題者布設的“陷阱”，也是拉分之處.因此，本題具有較好的效度和區分度.

二、從對角線的視角定義特殊四邊形

例2（2016年浙江·衢州卷）如圖5，我們把對角線互相垂直的四邊形叫作垂美四邊形.

（1）概念理解：如圖6，在四邊形ABCD中，AB=AD，CB=CD，問：四邊形ABCD是垂美四邊形嗎？請說明理由.

（2）性質探究：試探索垂美四邊形ABCD兩組對邊AB、CD與BC、AD之間的數量關系.

猜想結論（要求用文字語言敘述）.

寫出證明過程（畫出圖形，寫出已知、求證）.

（3）問題解決：如圖7，分別以Rt△ABC的直角邊AC和斜邊AB為邊向外作正方形ACFG和正方形ABDE，連接CE、BG、GE，已知AC=4，AB=5，求GE的長.

思路剖析：（1）連接AC、BD，利用垂直平分線判定即可證明AC⊥BD.

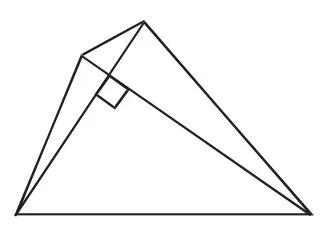
圖5

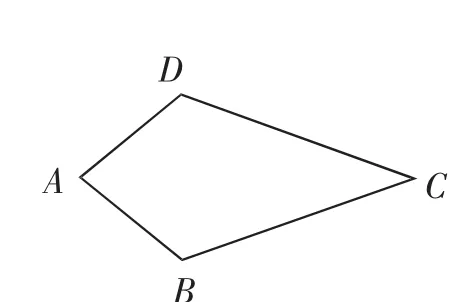
圖6

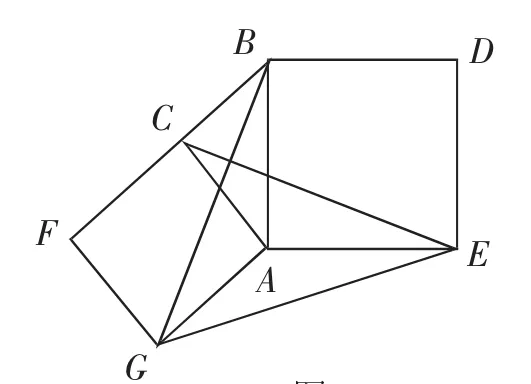
圖7

（2）猜想結論：垂美四邊形的兩組對邊的平方和相等.

如圖8，已知四邊形ABCD中，AC⊥BD，垂足為E.求證：AD2+BC2=AB2+CD2.

證明：利用勾股定理即可證明AD2+BC2=AB2+CD2成立.

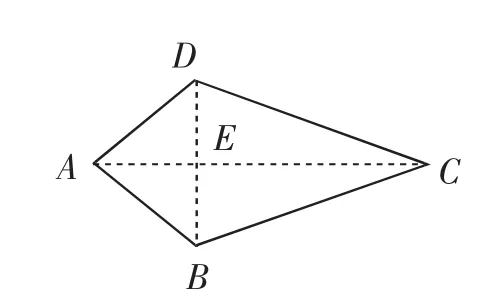
圖8

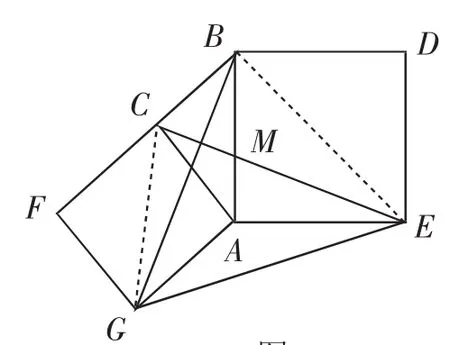
圖9

（3）如果考生不領會命題者的意圖，撇開垂美四邊形這條主線，忽視第（2）問的鋪墊，那么就會偏離解題方向而進入歧途.如果考生能順勢而為，在圖9中尋找哪四個點能構成垂美四邊形，通過觀察并猜想CE⊥BG，若能證明，就得到四邊形CGEB是垂美四邊形，再利用第（2）問的鋪墊，就能求出GE的長.在圖9中，連接CG、BE，可證△GAB≌△CAE（SAS），進而得∠ABG+∠AME=90°，所以CE⊥BG，即四邊形CGEB是垂美四邊形.由（2）得CG2+BE2=CB2+GE2.由題意可得BC=3，CG=4，BE=5，進而求得GE2=CG2+BE2-CB2=73，所以GE=.

評注：此題從對角線的視角定義了一個新概念“垂美四邊形”，以這個新概念為背景層層深入，梯度合理.第（1）問，謂之“起”.問題的起源，通過簡單的證明，加深對概念特征的理解.第（2）問，謂之“承”.承上啟下，通過畫圖、求證，既加深對概念的認識，又為第（3）問的探究做了很好的鋪墊.第（3）問，謂之“轉”.峰回路轉，問題考查的能力、基本思想和呈現方式都發生了很大變化.解決第（3）問的難點在于會識別“垂美四邊形”，再結合第（2）問的鋪墊逆向思考，進而計算解答.可見，第（3）問的設置是讓學生自主探究，不斷深入思考，從而提高學生分析問題、解決問題的能力，對學生思維能力的考查又上了一個臺階.

三、從一組對角的視角定義特殊四邊形

例3（2014年浙江·嘉興卷）類比梯形的定義，我們定義：有一組對角相等而另一組對角不相等的凸四邊形叫作“等對角四邊形”.

（1）已知：如圖10，四邊形ABCD是“等對角四邊形”，∠A≠∠C，∠A=70°，∠B=80°.求∠C、∠D的度數.

（2）在探究“等對角四邊形”性質時：

①小紅畫了一個“等對角四邊形”ABCD（如圖11），其中∠ABC=∠ADC，AB=AD，此時她發現CB=CD成立.請你證明此結論.

②由此小紅猜想：“對于任意‘等對角四邊形’，當一組鄰邊相等時，另一組鄰邊也相等”.你認為她的猜想正確嗎？若正確，請證明；若不正確，請舉出反例.

（3）已知：在“等對角四邊形”ABCD中，∠DAB=60°，

∠ABC=90°，AB=5，AD=4.求對角線AC的長.

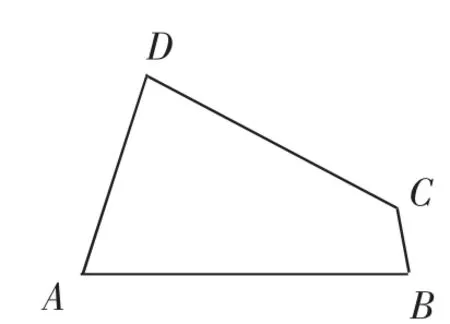
圖10

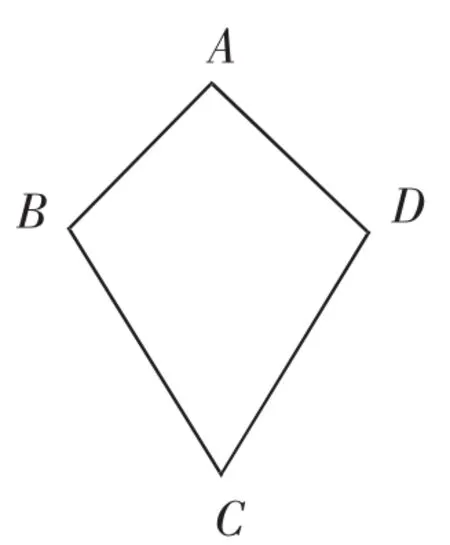
圖11

思路剖析：（1）利用“等對角四邊形”這個概念進行直接計算.因為∠A≠∠C，所以∠D=∠B=80°，∠C=130°.

（2）①如圖12，連接BD，容易證明CB=CD成立.

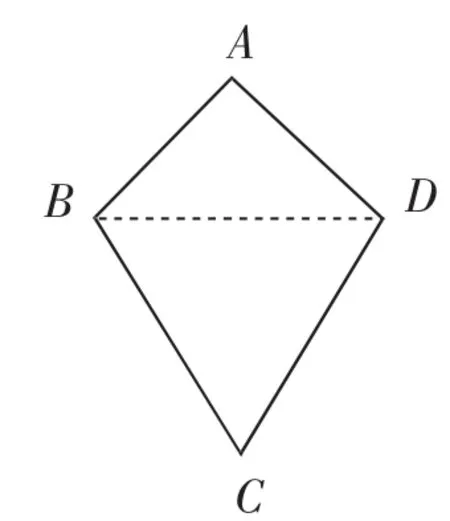
圖12

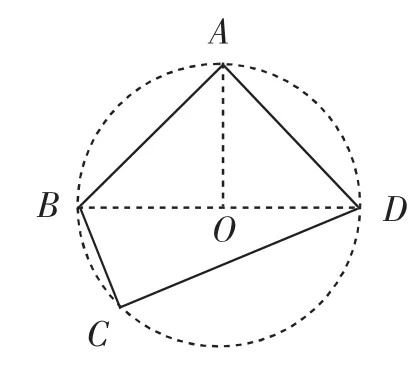
圖13

②不正確.舉一個反例即可，如圖13，∠A=∠C=90°，AB=AD，但CB≠CD.其實，只要借助輔助圓，構造有公共斜邊的兩個直角三角形，這些圖形在平時很常見，關鍵是考試時能否迅速檢索出積累的基本圖形.

（3）解答此題，要深刻領悟“等對角四邊形”的概念.

①如圖14，當∠ADC=∠ABC=90°時，延長AD、BC相交于點E，易得AE=10，進而求得DE=6，CD=2，所以AC==2.

②如圖15，當∠BCD=∠DAB=60°時，過點D作DE⊥AB于點E，DF⊥BC于點F.

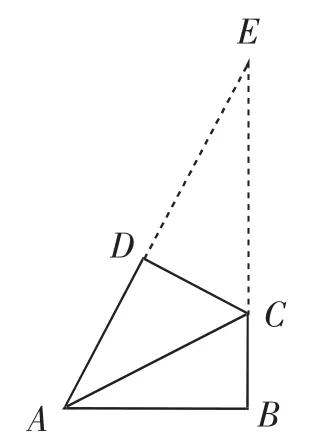
圖14

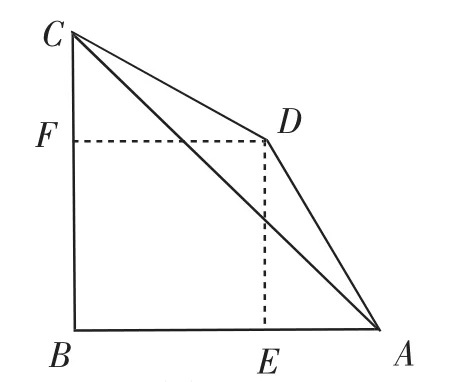
圖15

評注：此題是從一組對角的視角給定一個新定義“等對角四邊形”的探究型試題，通過一題多探，拾級而上，層層深入，為不同程度的學生展示自己的數學才華創設了探究平臺.第（1）問通過計算等對角四邊形的內角，使學生對等對角的概念加深了認識；第（2）問與第（1）問相比，雖然表象發生了變化，但本質不變，只要求學生對新概念有精準理解；第（3）問是本題的精華，命題者巧妙地把等對角四邊形的概念隱藏在無圖的敘述中，考查學生理解新知、運用新知的能力.此題匯集了三角形、勾股定理、四邊形等知識，滲透了轉化、分類討論等數學思想，立意新穎.該題考查的角度多樣，三個問題在難度上逐步加大，對學生知識遷移、信息閱讀、自主探索和解決問題的能力都是一種挑戰.這一系列探究在本質上就是“數學化”的過程，經歷這些過程是學生獲取“四能”的根本途徑.

由以上幾例可以看出，以四邊形為背景的新定義型中考試題能較好地體現新課程標準的基本理念，注重培養學生的數學思考、數學能力和數學素養.同時，此類試題并不神秘，表面上是我們沒有見過的問題，但只要理解了新定義并緊扣新定義，就將其轉化為我們熟悉的幾何問題.這類問題具有探究價值，對運用新知識解決問題的能力提出了較高的要求，具有良好的效度和區分度.這要求我們在平時學習中夯實“四基”，注重能力和數學思想方法的學習及應用意識的培養，以不變應萬變.