挖掘課本習(xí)題價值 促進學(xué)生深度思考

☉湖北省武漢市漢陽區(qū)教育局教科中心 桂文通

人教版九年級數(shù)學(xué)教材（下冊）第58頁有如下一道習(xí)題，為方便我們稱為引例.

引例 如圖1，一塊材料的形狀是銳角三角形ABC，邊BC=120mm，高AD=80mm，把它加工成正方形零件，使正方形的一邊在BC上，其余兩個頂點分別在AB，AC上，這個正方形零件的邊長是多少？

本文想結(jié)合引例，就如何挖掘課題習(xí)題的價值，構(gòu)建一類問題解決的基本模式，引導(dǎo)學(xué)生進行深度思考作一點探討.

一、“出入相補”創(chuàng)新解法

我們可以運用下面兩種方法解決引例：

方法1（常規(guī)解法）：設(shè)加工成的正方形為EFHG，邊長為xmm，邊GH在BC上，頂點E，F(xiàn)分別在AB，AC上，高線AD與EF相交于點K.

答：加工成的正方形零件的邊長為48mm.

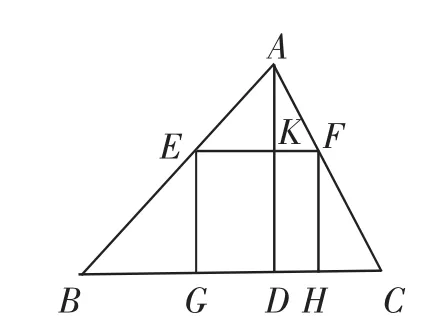
圖1

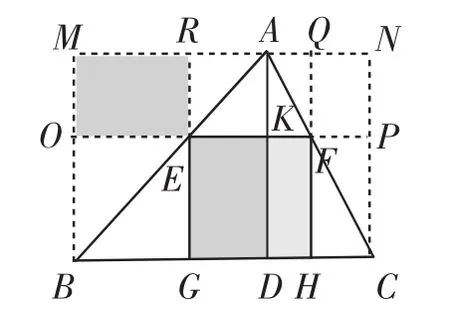
圖2

方法2（出入相補法）：將圖1補成矩形BCNM，如圖2，圖中的面積關(guān)系有：S△ARE=S△AKE，S△ABD=S△ABM，S△OBE=S△GBE，

所以S矩形OMRE=S矩形EGDK.

同理：S矩形QNPF=S矩形KFHD.

于是S矩形OMRE+S矩形QNPF=S正方形EFHG.

設(shè)GE=EF=x，則MR+QN=120-x，OM=80-x，列方程得x2=（80-x）（120-x），解得x=48.

比較兩種解法：方法1看似比方法2簡捷，但兩種方法的知識儲備是不一樣的，方法1需要運用相似三角形的判定與性質(zhì)等知識；解法2的門檻要低得多，只需運用面積的計算即可.方法2給人一種意外的驚喜，讓人感受到數(shù)學(xué)方法的樸實之美，能夠激發(fā)學(xué)生學(xué)習(xí)的興趣，感受學(xué)習(xí)數(shù)學(xué)的樂趣.其實方法2運用了中國古代數(shù)學(xué)中“出入相補原理”，吳文俊院士在《出入相補原理》一文中指出：“一個平面圖形從一處移置他處，面積不變.又若把圖形分割成若干塊，那么各部分面積的和等于原來圖形的面積，因而圖形移置前后諸面積間的和、差有簡單的相等關(guān)系.”

借鑒古人的思想方法來解決數(shù)學(xué)問題，能夠拓寬學(xué)生的視野，培養(yǎng)發(fā)散思維，讓學(xué)生感受數(shù)學(xué)思想方法的力量，從而啟迪智慧增強信心，也能體現(xiàn)數(shù)學(xué)的文化意義.

二、“以退為進”探求作法

如果此題中的正方形沒有畫出，我們是否可以借用尺規(guī)畫出呢？

要求作一個正方形，使它的四個頂點在△ABC的三條邊上.可以如下思考：“只保留條件的一部分，而丟掉其他部分.”（波利亞語）很顯然畫出一個有兩個頂點在△ABC邊上的正方形很容易，畫三個頂點在△ABC邊上的正方形也可以.

于是我們可以嘗試畫出有三個頂點在△ABC邊上的正方形，如圖3，4，5.

圖3

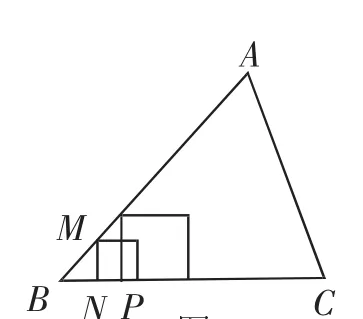
圖4

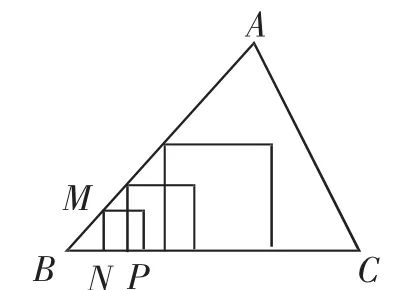
圖5

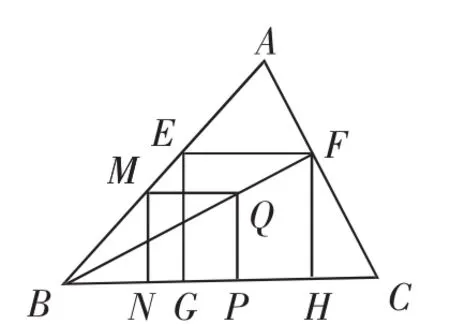
圖6

從圖3，4，5中，我們可以觀察并猜想到這些正方形的第四個頂點排列規(guī)律：在同一條直線上.為了使第四個頂點在△ABC的邊上，我們用圖6，作法如下：

（1）作正方形MNPQ，使它的頂點M，N，P在邊AB和BC上.

（2）作射線BQ交邊AC于點F.

（3）過點F分別作EF∥BC交AB于點E，作FH⊥BC，垂足為點H，過點E作EG⊥BC，垂足為點G.

由作法知四邊EFHG是矩形，而在圖6中，由EF∥MQ，F(xiàn)H∥PQ，得.又因為MQ=PQ，得EF=FH.所以矩形EFHG是正方形.

其實，上面的作法采取了位似變換作圖法.通過作圖嘗試，讓學(xué)生觀察出第四個頂點的軌跡，體現(xiàn)了“探索是數(shù)學(xué)的生命線”教學(xué)策略；通過弱化條件，可以向?qū)W生滲透“以退為進”的數(shù)學(xué)思想.數(shù)學(xué)家華羅庚對“以退為進”的數(shù)學(xué)思想解釋為：“善于‘退’，足夠地‘退’，‘退’到最原始而不失重要的地方，是學(xué)好數(shù)學(xué)的一個訣竅.”

三、橫向變式構(gòu)建模式

例1 如果原題中所要加工的零件只是一個矩形EFHG，如圖7，此矩形零件的兩條邊長不能確定，但這個矩形面積有最大值，求達(dá)到這個最大值時矩形零件的兩條邊長．

分析與解：設(shè)EF=xmm，根據(jù)相似三角形對應(yīng)高的比等于相似比列出比例式，并用x表示出EG，然后根據(jù)矩形的面積公式列式計算，再根據(jù)二次函數(shù)的最值問題解答．

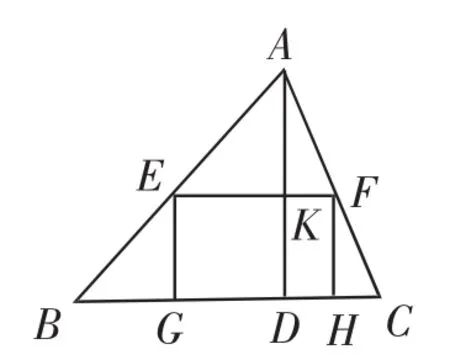
圖7

所以S的最大值為2400mm2，此時EF=60mm，EG=40mm．

價值分析：本題突出了相似三角形性質(zhì)的應(yīng)用，通過面積與有關(guān)線段的關(guān)系，建立二次函數(shù)模型，再利用配方法求出二次函數(shù)的最值．從問題的解決中，我們可以提煉一個重要結(jié)論：當(dāng)EF是△ABC的中位線時，矩形EFHG的面積最大.

應(yīng)用1 （鹽城中考題）（1）如圖8，是一張直角三角形紙片，∠B=90°，小明想從中剪出一個以∠B為內(nèi)角且面積最大的矩形，經(jīng)過多次操作發(fā)現(xiàn)，當(dāng)沿著中位線DE，EF剪下時，所得的矩形的面積最大，隨后，他通過證明驗證了其正確性，并得出：矩形的最大面積與原三角形面積的比值為______ .

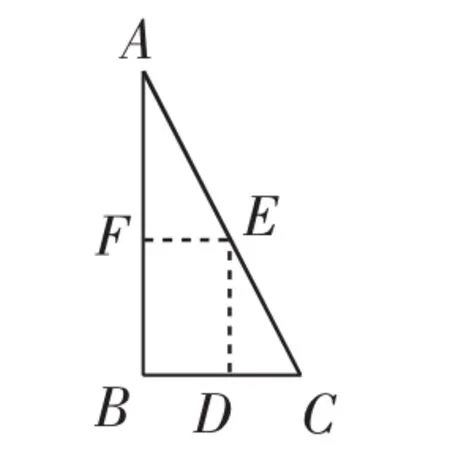
圖8

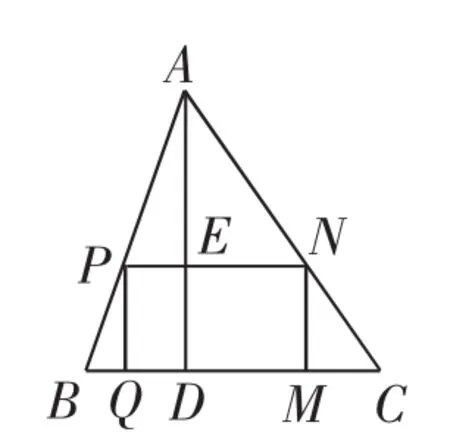
圖9

（2）如圖9，在△ABC中，BC=a，BC邊上的高AD=h，矩形PQMN的頂點P，N分別在邊AB，AC上，頂點Q，M在邊BC上，求矩形PQMN面積的最大值為______（用含a，h的代數(shù)式表示）.

（3）如圖10，有一塊“缺角矩形”ABCDE，AB=32，BC=40，AE=20，CD=16，小明從中剪出了一個面積最大的矩形（∠B為所剪出矩形的內(nèi)角），求該矩形的面積．

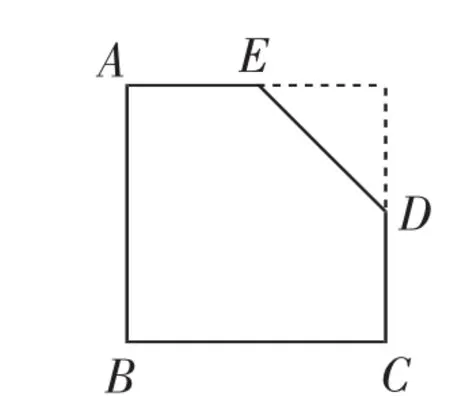
圖10

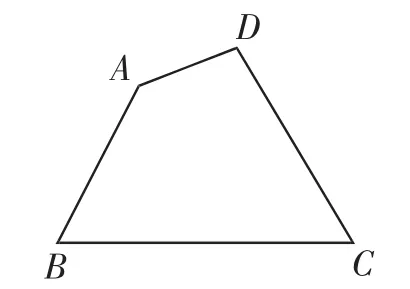
圖11

（4）如圖11，現(xiàn)有一塊四邊形的木板余料ABCD，經(jīng)測量AB=50cm，BC=108cm，CD=60cm，且tanB=tanC=，木匠徐師傅從這塊余料中裁出了頂點M，N在邊BC上且面積最大的矩形PQMN，求該矩形的面積．

分析與解：（1）、（2）就是例2結(jié)論的一般化，答案分別為：-.

（3）將圖10補成圖8的形式，如圖12，延長BA，DE交于點F，延長BC，ED交于點G，延長AE，CD交于點H，取BF中點I，F(xiàn)G的中點K.注意要說明中位線IK的兩端點在線段AB和DE上，可求該矩形的面積為720.

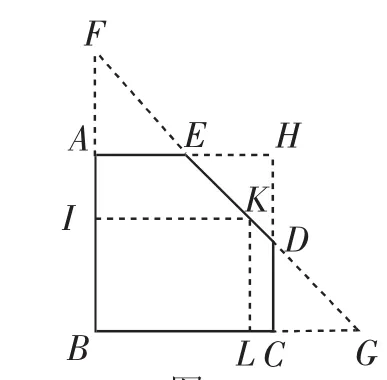
圖12

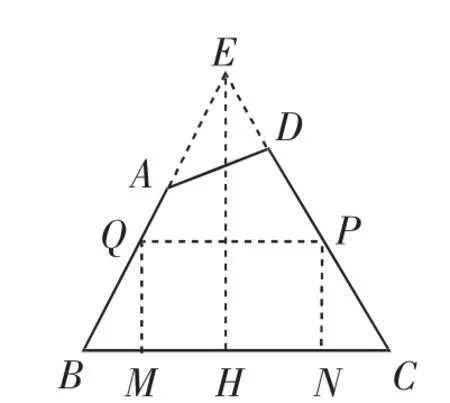
圖13

（4）同（3），將圖11補成圖9的形式，如圖13，延長BA，CD交于點E，過點E作EH⊥BC于點H，再作中位線PQ，作矩形PQMN，可求該矩形的面積為1944cm2.

例1給我們分別提供了解決不同問題的基本模式.數(shù)學(xué)家笛卡爾也說過“我所解決的每一個問題都將成為一個模式，以用于解決其他相關(guān)問題”，我們的解題教學(xué)應(yīng)該多提煉模式、多積累模式，讓學(xué)生自覺地運用模式去解決新的問題，從而提高解題效率.

四、縱向引申深度拓展

例2 如圖14，一塊材料的形狀是銳角三角形ABC，三邊分別為a，b，c，且a＞b＞c，把它加工成正方形零件，使正方形的四個頂點都在三角形邊上，問正方形的兩個頂點放在哪條邊上可使加工出來正方形零件的面積最大？

分 析與 解 ： 設(shè)a，b，c三邊上的高分別為ha，hb，hc，△ABC的面積為S，落在a，b，c三邊上的正方形邊長分別為xa，xb，xc.

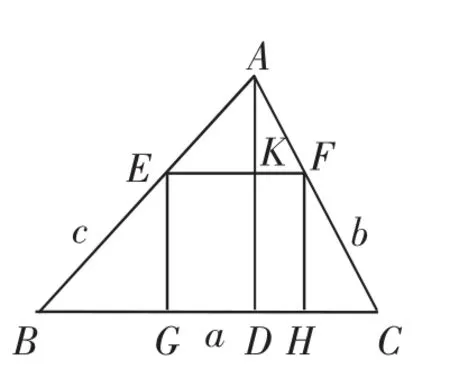
圖14

又因為a＞b，于是xa＜xb.

同理xb＜xc，從而xa＜xb＜xc.

所以當(dāng)正方形的兩個頂點放在最短邊上可使正方形零件面積最大.

從例2我們可以得到一個這樣的命題，等邊三角形的三個內(nèi)接正方形的面積相等.反之，它的逆命題呢？即一個三角形的三個內(nèi)接正方形的面積相等，則這個三角形是等邊三角形.這個命題直觀上感覺是正確的，但需要我們進行嚴(yán)格證明.

例3 如圖14，設(shè)△ABC三邊上的三個內(nèi)接正方形的面積相等，求證：△ABC為等邊三角形.（江蘇省初中數(shù)學(xué)競賽題）

由已知xa=xb=xc，所以

又因為aha=bhb=chc，所以a+ha=b+hb=c+hc

因為t≠0，所以t2-kt+2S=0，（2）

故a，b，c是二次方程（2）的根，但二次方程至多只有兩個相異的根，所以a，b，c中某兩數(shù)必相同，不妨設(shè)a=b.

因為a-c≠0，所以ac=2S=aha，故c=ha.這樣△ABC是∠B為直角的直角三角形，b為斜邊，于是b＞a，這與a=b矛盾，故a=c.

所以a=b=c，即△ABC為等邊三角形.

例2通過縱向引申，開放思維形式，分類討論來探求結(jié)論的一般性；例3是對例2的一個引申結(jié)論的逆命題的探索.兩個例題的探究過程都能引發(fā)學(xué)生積極主動地深度思考，需要很強的綜合問題解決能力，除了運用引例所蘊含的基本知識和方法外，還綜合運用了許多代數(shù)的方法，比如例2的作差比較法、因式分解法；例3中一元二次方程的基本理論和反證法思想的運用.這些思維訓(xùn)練，很好地提升了學(xué)生的數(shù)學(xué)素養(yǎng).

教材是教學(xué)的根本，是最經(jīng)濟、實惠的題庫，蘊含著取之不盡，用之不竭的題源，教師用好教材可以引發(fā)學(xué)生深度思考，為學(xué)生打開一扇天窗，促進他們的核心素養(yǎng)的提高.習(xí)題教學(xué)經(jīng)常做到幾問：該題涉及哪些知識點、以什么為主？教學(xué)難點在何處？有哪些基本模型和基本方法？有哪些變式或拓展？如何挖掘出其中蘊涵的數(shù)學(xué)思想方法等？如何將它的知識價值、教育價值的最大化.唯有如此，才能理深刻理解教材，才能讓學(xué)生脫離題海，回歸數(shù)學(xué)教學(xué)本質(zhì).