注重教學過程設計,提高學生課堂參與
唐露溢
(四川省犍為縣羅城初級中學,四川 犍為)
2004年12月25日,教育部正式頒布了《中小學教師教育技術能力標準》,它的實施使中小學教師的專業能力有了第一個標準。在《中小學教師教育技術能力標準》中對教學設計的定義為:教學設計又稱為教學系統設計,是指主要依據教學理論、學習理論和傳播理論,運用系統科學的方法,對教學目標、教學內容、教學評價等教學要素和教學環節進行分析、計劃并作出具體安排的過程。對教師的能力有很多要求,而且每個要求之間有著千絲萬縷的聯系,不可分割,但我想著重談談教學過程設計能力。
一、具有層次,節奏流暢
教師在教學過程中根據每個班同學的理解程度、知識基礎,由淺入深、循序漸進,控制好層次,把握好節奏,可以讓沉悶的教學更有活力,讓學生更想參與,更容易參與。
案例一:華東師大版七年級數學上冊已經讓學生開始接觸整體代入法,但是如何讓學生容易理解整體的思想,并轉化成運用,每個教師根據自己的經驗和自己學生的情況都有一套自己的套路。以下是我給七年級學生講整體代入法的步驟。
步驟一:練習:若 A=4,B=3,則 A2-2B=_________。
步驟二:探索:例 1:若 m+n=4,mn=3,求(m+n)2-2mn的值。模仿例1自己編寫一道相似的題。
步驟三:練習 2:已知 a、b 互為相反數,c、d 互為倒數,求 2(a+b+cd)的值。
步驟四:例2:若a-3b=-3,則代數式5-a+3b的值為___。
步驟五:例3:若x+5y=4,求代數式2x+10y+7的值。
步驟七:我想和___做對手。我為他出的題是___。
學生通過層層抽絲剝繭的學習,體驗到成功的喜悅,積極地參與到活動中,體現自己的價值。
二、符合學生學習規律
學生的認知都是由淺入深、由具體到抽象、由感性到理性,但是不同的學生認知也有不同,所以對同一事物的看法也會不同。在教學過程中,根據自己對學生的了解,制定符合自己學生的教學過程,讓學生在課堂上喜歡參與。
案例二:華東師大版八年級數學上冊第14章勾股定理中,為了引入勾股定理先研究直角三角形三邊的關系。
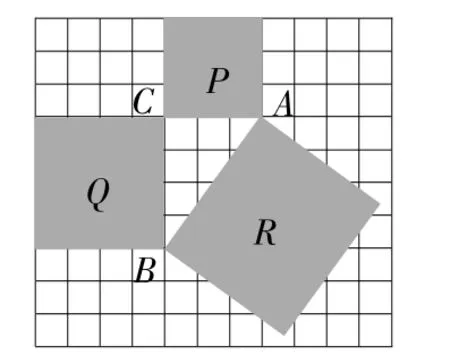
試一試:觀察圖,如果每一小方格表示1平方厘米,那么可以得到:正方形P的面積=___平方厘米,正方形Q的面積=___平方厘米,正方形R的面積=___平方厘米,我們發現,正方形P、Q、R的面積之間的關系是___。由此,我們得出Rt△ABC的三邊長度之間的關系是____。概括出勾股定理以后再根據弦圖用面積進行證明。
三、活動目標適度且有吸引力
學生千差萬別,層次不一,深入地了解自己的學生,在教學中建立適合他們的教學要求和目標,讓他們跳一跳就能完成學習任務,學生內心充滿成就感,讓刻板的數學吸引他們參與其中。有一部分學生由于小學時期對于算數思想根深蒂固,在學習代數時不容易轉變,針對這部分學生,如果先用數字再用字母,會讓他們在學習中更容易接受,更有興趣,能主動參與,完成教學目標。
案例三:探索百分率問題:
探索:1.某產品去年的產值為100件,今年的增長率為20%,則今年的產值為100(1+20%),如果明年的增長率也為20%,明年的產值為 100(1+20%)(1+20%)=100(1+20%)2
2.某產品去年的產值為a件,今年的增長率為x,則今年的產值為 a(1+x),如果明年的增長率也為 x,明年的產值為 a(1+x)(1+x)=a(1+x)2
歸納:如果某個量原來的值為a,每次增長率為x,則增長(降低)1 次后的值為 b1,a(1±x)=b1,增長(降低)2 次后的值為 b2,a(1±x)2=b2,增長(降低)3 次后的值為 b3,a(1±x)3=b3,增長(降低)n次后的值為 b,a(1±x)n=b,如果某個量原來的值為 a,每次增長率為 x,增長 n 次后的值為 b,則 a(1±x)n=b,其中 a代表基數,x代表百分率,n代表變化次數,b代表連續變化結果。
四、恰當運用現代教育技術
快速發展的現代信息化技術,為我們的數學教學提供了很多方便,也有很多應用軟件為我們的數學教學提供了方便的平臺。但是每一種技術都有它的優缺點,如何更好地利用它的優點,揚長避短,我們必須對它有很深入的了解,能在PPT、白板、微課等軟件之間運用自如來回切換,選擇適合學生的、適合教學內容的,讓它們為我所用,更大地發揮時間、空間的作用,提高學生對整堂課的關注度,并能把這種關注持續到課堂之后。

