關于四色猜想的幾何證明和其在多維空間推論的構造及可能性探討
中國人民大學附屬中學 滕笑非
四色猜想,又稱四色問題,是世界三大數學猜想之一,最先是由一位叫弗朗西斯·古德里的英國大學生提出的。四色猜想的具體內容是:“任何一張地圖使用四種顏色就能使具有共同邊界的國家著上不同的顏色。”也就是說在不引起混淆的情況下,一張地圖只需要四種顏色來標記。
用數學語言表示即:“將平面任意地細分為不重疊的區域,每一個區域總可以用1、2、3、4這四個數字之一來標記而不會使相鄰的兩個區域得到相同的數字。”這里所指的相鄰區域是指有一整段邊界是公共的。如果兩個區域只相交于一點或有限多點就不叫相鄰,因為用同種顏色給它們著色不會引起混淆。
作為世界三大數學猜想之一,四色猜想的證明一直是一個引人入勝的題目。自從它在1852年被提出,無數數學家都嘗試證明四色猜想,但都無功而返。直到1976年6月,通過電子計算機1200小時中做的100億個判斷,證明了確實沒有任何一張地圖需要用5種顏色,四色猜想終于被證明。但是計算機證明終究不是理論證明,雖然遍歷了100億個判例全部通過,但這并不能說明不存在極端反例。在此,本文給出四色猜想的平面幾何證明方法。
一、四色猜想的幾何證明
首先,建立數學模型。之所以需要四種顏色才能區分,是因為存在四個兩兩相交的區域,這樣我們必須讓任何一個區域的顏色都與另三個不同。如果對于任意四個兩兩相交的區域A、B、C、D,存在第五個區域E,使E與A、B、C、D均相交,則E需要用第五種顏色染色。換言之,若要證明四色猜想,只需證明不存在五個兩兩相交的平面圖形即可。
因為在四色猜想中,區域的形狀并不重要,重要的是區域之間的相交關系,所以我們采用了理想模型簡化問題。將任何平面幾何圖形理想化為圓,將區域之間的相交表示為兩圓相切,則任意兩個有公共邊的凸多邊形可以表示為圓A外切圓B;任意兩個有公共邊的凹多邊形A、B也可以表示成圓A外切圓B(如圖1);任意凸多邊形A和凹多邊形B有公共邊可以表示為圓A內切圓B(如圖2)。另外,不存在圓C同時內切圓A、B且切點均為O的情況,因為雖然這樣圓A、B、C滿足兩兩相切,但在非理想情況下,A、C區域并不存在公共邊(如圖3)。我將這樣的圓C定義為二次內切圓,易得這樣的理想模型中不應存在二次內切圓。這樣我們就通過理想化模型表示了平面圖形之間的位置關系,我們需要證明的命題也轉化為“在沒有二次內切圓的情況下,不存在五個兩兩相切的圓”。
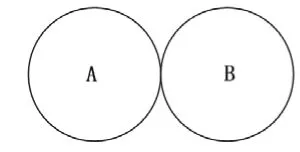
圖1

圖2

圖3
由于對于任意給定閉合區域和給定個數的給定圓,若在該區域內存在一圓使其與所有已知圓相切,則該圓一定是固定唯一的;對于任意給定開放區域和給定個數的給定圓,若在該區域內存在一圓使其與所有已知圓相切,則該切點一定是固定唯一的。所以我們可以用BFS(廣度優先搜索)算法,遍歷所有區域,判斷該區域內能否存在一個滿足與所有已知圓相切,直到所有可能性都不能再添加進去的新的圓后結束遍歷,即可判斷最多能存在幾個兩兩相切的圓。
BFS遍歷過程如圖4所示:

圖4
綜上,在不存在二次內切圓的情況下,不存在五個兩兩相切的圓,即平面內不存在五個兩兩之間存在公共邊的圖形,四色猜想得證。
二、四色猜想在其他已知維度內的推廣
若要進行這個推廣,首先要嚴格定義n維圖形(n∈N+)相交。不難發現,在一維空間中,相交的定義為共端點(點認為是零維面);在二維空間中,相交的定義不再使用存在公共點而是改為公共邊(邊認為是一維面);三維空間中,相交的定義則變成至少有一部分面積接觸,換言之即是存在公共面。也就是說,對于n為空間(n∈N+)中的n維圖形,相交的判定應為存在公共的(n-1)維面。
在這個定義下,我們發現:
一維空間中兩兩相交的一維圖形最多只存在兩個,即只需要2種顏色即可染色。
二維空間中兩兩相交的二維圖形最多只存在四個,即只需要4種顏色即可染色。
三維空間中兩兩相交的三維圖形最多只存在八個,即只需要8種顏色即可染色。
以上均通過與四色猜想幾何證明相似的理想模型假設法證明。
三、關于四色猜想在多維空間推論的猜想
根據四色猜想在已知維度內推廣的結論,我猜想該推廣在n維空間(n∈N+)中均適用,且滿足“n維空間中兩兩共(n-1)維面的n維圖形最多只存在2n個,即只需要2n種顏色即可染色”。
四、關于四色猜想在多維空間內推論猜想的合理性討論
多維空間不同于三維以下空間,有幾何工具并且可以通過人腦直接想象。對于四維及以上空間的研究只能停留在純代數領域,此處引入拓撲學原理進行討論。
拓撲學是研究幾何圖形或空間在連續改變形狀后還能保持不變的一些性質的學科,它只考慮物體間的位置關系而不考慮它們的形狀和大小。
在拓撲學里不討論兩個圖形全等的概念,但是討論拓撲等價的概念。比如,圓和方形、三角形的形狀、大小不同,但在拓撲變換下,它們都是等價圖形;足球和橄欖球,也是等價的——從拓撲學的角度看,它們的拓撲結構是完全一樣的。
在拓撲學原理的前提下,我們可以將任意維度的幾何圖形簡化為一個節點,如果兩節點之間存在一條無向邊則稱他們是相交的,這種無向邊是一種邏輯關系,即兩兩相交的n個圖形滿足:這n個節點兩兩之間存在一條無向邊,且這些無向邊沒有交叉的,否則說明其中一種連通關系是建立在另一種連通關系之上而非直接相交的。
如此一來,我們將高維度難以想象和計算的問題轉化為求給定維度下最多能存在多少個點,使得這些點兩兩連線互不相交?
為了方便表示,我們定義數列{an},其中第i項ai表示在i維空間中,滿足任意兩點連線互不相交的最大點的個數。這表示i維空間中最多存在ai個兩兩相交的i維圖形,也就是需要最多ai種顏色即可完全染色i維空間的任意連續圖形。
根據我們的猜想,{ai}的通項公式為ai=2i(i∈N+)。
下面不加證明地給出在i維空間中,構造2i個點,使任意兩點連線互不相交的方法:
定義:n維空間中,滿足命題題意的最大數量的點組成的n維點陣成為n維時的最大點陣。
i=1時,顯然a1=2。若放入第三個點,在一維空間中勢必構成三點共線,使得點之間連線相互重疊。i=1時的最大點陣如圖5所示。
對于任意i≥2,該i維點陣中一定存在若干個(i-1)維面,若任意(i-1)維面的點數量小于ai-1,則該(i-1)維面一定能再放入一個點,若數量大于ai-1,則該(i-1)維平面一定與命題矛盾。即當且僅當該點陣的每個(i-1)維平面都是(i-1)維時的最大點陣時,該點陣為i維的最大點陣。
i=2時的最大點陣如圖6所示,a2=4。

圖5

圖6
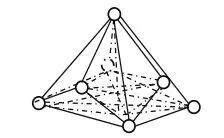
圖7
i>2時,任取(i-1)維最大點陣一點,將其以第i維度的方向平移。不難想象,該操作會構造出新的(ai-1-1)個異于原最大點陣的(i-1)維面,此時的ai-1個點構成一個有ai-1個(i-1)維面的i維圖形。在所得的i維圖形的每個(i-1)維面上各任意選取一個面內點,則會構造出ai-1個新點,這2ai-1個點即為i維的最大點陣。由構造過程可得,對任意 i>2,ai=2ai-1。
i=3時的最大點陣如圖7所示,與猜想相符。
由于知識水平和技術手段的限制,本文只能給出上述構造方法,但無法嚴格證明。目前的想法是采用計算機的高維數組儲存多參數變量進行高位計算來驗算其可行性,但是遍歷算法,驗算n維構造的估算時間復雜度約O(n2·22n),以目前的技術,該時間復雜度仍然過高。希望將來可以開發更先進的針對多維空間的算法來證明本文對于四色猜想在多維空間推論的猜想。

