拋物線中一個定點問題的探究之旅

福建省龍巖市第一中學 (364000)

劉文娟

圓錐曲線綜合問題是解析幾何的核心內容，是歷年高考數學的重要考點之一，也是復習備考中較難突破的難點之一.對于圓錐曲線的綜合問題，由于含字母且運算量大，加之學生能熟練使用的方法比較單一，所以在求解過程中讓許多學生倍感困惑.在高考復習中，針對圓錐曲線的某些綜合問題，不能僅僅停留在對問題的求解上，教師要善于適時引導學生對問題解決后的再研究、再發現.這樣，既能培養學生的靈活解決數學問題的能力，又可以避免由于孤立靜止地思考問題所帶來思維的局限性和片面性，還能較好地激發學生自身對數學問題的探究能力，提升研究水平.這對于訓練學生數學思維的敏捷性與靈活性是有益的.

筆者以下面的這道圓錐曲線綜合問題為例，開啟了拋物線中一個定點問題的探究之旅.

1.探究背景

筆者對學生的解答情況進行了分析，發現學生解題思路很好，只是未能到最終的結果.

思路2：先設M(-m,yM)、N(-m,yN)，寫出以MN為直徑的圓方程，同樣聯立直線方程x=ty+m與拋物線方程，得到一個一元二次方程，利用韋達定理得到y1+y2,y1·y2但由于忽略題目當中各變量間的關系，無法將圓方程繼續整理化簡，也放棄了.

筆者根據前面的解題思路繼續講評，正確解答：

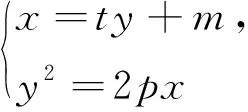
設M(-m,yM)、N(-m,yN)，則以MN為直徑的圓方程(-m-x)2+(yM-y)(yN-y)=0，整理得x2+2mx+m2+y2-(yM+yN)y+yMyN=0，

令y=0，x2+2mx+m2+yMyN=0.

此題講評完，學生感慨：看來“成功就是再堅持一下的努力中”真是沒錯.

課上，筆者又提問學生：反過來，我們是否能根據“以MN為直徑的圓被x軸截得的弦長為定值

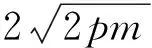
思考一段時間后，就有學生給出肯定答案，并根據剛才的推導過程，說明緣由.從而我們得到

講完這道例題,筆者在想:是否還有其它的關于這個定點的等價條件?為完成教學進度,筆者課題上沒有過多地思考,只給學生留下一句話:同學們把這道題作為一個特殊的題目記錄在筆記中,課后有興趣的同學可以交流探討.但此時筆者的心中卻已燃起了探究的火花.

2．探究發現

課后筆者再次探究這道題目時,突然想起在課本上有一道類似的題目,湖南教育出版社《數學》(選修1-1文科)第79頁復習二第19題,也是探究拋物線中的定點問題.

設直線l與拋物線y2=2px(p>0)交于A(x1,y1),B(x2,y2)兩點，其中y1>y2.

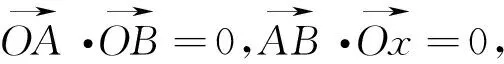
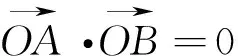
由這道例題，筆者再深入分析，發現這樣一個更一般性的結論：

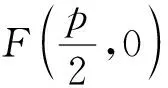
對于上面兩道題的分析，給了筆者啟發，在平時的教學過程中，做有心人，筆者又得到了其他幾個結論.

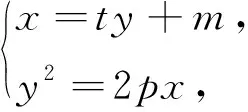
(充分性略)

結論4 設不垂直于x軸的直線l與拋物線y2=2px(p>0)交于A(x1,y1),B(x2,y2)兩點，點M′(-m,0)，則直線l過點(m,0)(m>0)的充要條件是x軸為∠AM′B的角平分線.

結論5 設直線l與拋物線y2=2px(p>0)交于A(x1,y1),B(x2,y2)兩點，則直線l過點(m,0)的充要條件是y1y2=-2pm.

還有下面兩種特殊情況：

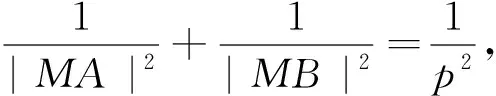
除了從結論1-結論5中得到直線過焦點的等價條件外，還有如下的結論：

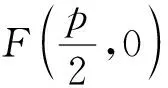
3.反思總結

教師在平時做題時，可以多做一些問題的拓展探究，并在講題時適當引導學生思考探索，教師在教學中的多引導，促進學生多思考，培養學生的發散思維，讓學生看到解題的“有趣”，體會數學的魅力.

在對拋物線中一個定點問題的探究過程中，給筆者的啟發就是，我們要在平時的教與學的過程中做“有心人”，我們做的每一道題，都是專家經驗的積累、智慧的結晶，所以不是做完一道題就結束了解題，我們要深入研究，也要引導學生利用好做過的題，善于積累將會起到事半功倍的作用，同時也可以挖掘學生的潛能，提高學習的興趣.