初探“五步解題法”在幾何解題教學中的運用
林日榮
幾何難學,幾何難教,是農村普通初中學生和老師都有共識的地方,究其原因在于幾何的抽象,需要學生運用清晰的邏輯思維梳理紛繁的條件來進行演繹證明。當前,《義務教育數學課程標準(2011年版)》(以下簡稱《標準》)指出:“數學教學應從學生實際出發,創設有助于學生自主學習的問題情境,引導學生通過實踐、思考、探索、交流等,獲得數學的基礎知識、基本技能、基本思想、基本活動經驗,促使學生主動地、富有個性地學習,不斷地提高發現問題和提出問題的能力、分析問題和解決問題的能力。”從中我們可以了解到,《標準》強調了數學教學要針對學生學習水平的實際情況,引導學生在學習過程中獲得解決問題的技能,提高分析、解決問題的能力。
幾何解題教學,學生聽不懂,或者就算聽懂了也不會舉一反三,但若學生能掌握一套可操作性強的方法,便可以幫他們理清條件,理順思路,順利解題。五步解題法便是這樣的一種方法,其可操作性強,能把抽象邏輯的幾何解題變為直觀形象,能讓學生看得到、摸得著地解決。
一、五步解題法教學過程展示
針對人教版八年級數學上冊第十一章《三角形》中三角形的高、角平分線、內角和、內外角關系等知識的綜合運用,現以下面的題目為例運用五步解題法進行教學,以點帶面,舉一反三,讓學生在學習中生成解題技巧,獲得成功體驗,體會解題樂趣。
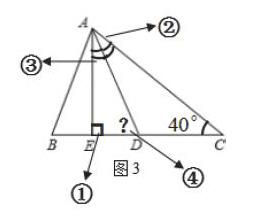
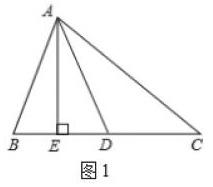
例:如圖1,若AE是△ABC中BC邊上的高,∠EAC的角平分線AD交BC于點D,∠C=40°,求∠ADE的度數.
1.審題
開口讀題,高度集中學生的注意力,促使學生深刻感知題目的已知條件和所求,從中提取有效的條件,保證不遺漏,達到分析和理解題意的目的。讀題過程中,進一步要求學生進行標注,即在有效的條件下劃線,并將文字語言轉換為符號語言。
2.標記
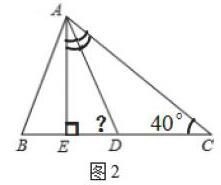
如圖2,審題過后,學生的邏輯推理意識已經喚醒,指導學生利用精準的符號在圖形里進行標記,適時引導學生將抽象的符號語言在圖形里直觀形象展示,讓學生看得到、摸得著,體驗數形結合的重要性。
3.判斷
對應審題時所做的標注,判斷考查的知識點,結合圖中標記的位置,利用幾何符號語言表達出邏輯推理中的因果關系。
師:∵AE⊥BC;生:∴∠AEC=90°.
師:∵AD平分∠EAC;生:∴∠CAD=∠EAD=1/2∠EAC.
師:要求出∠ADE=?,一個三角形已知一角度數,求另一角度數,還差什么條件?帶出求∠DAE=?
……
師:想要求得∠DAE的度數,要先求誰?條件夠嗎?引導學生把∠EAC所在的三角形找出來,發現已有∠C=40°,∠AEC=90°,利用三角形內角和定理即可以求得∠EAC的度數。
如圖3,引導學生進行知識點判斷,既提升了他們逆向推理的水平,也促使他們頭腦中的解題邏輯順序清晰起來,進一步在圖中標注上數字序號,為寫解題過程理順了次序。
4.寫過程
對應判斷時標注的次序序號,用符號語言把已經初步分解的解題過程寫出來。
① 解:∵AE⊥BC
∴∠AEC=90°
② ∵∠C=40°
∴∠EAC=50°
③ ∵AD平分∠EAC
∴∠CAD=∠EAD= ∠EAC=25°
④ ∵∠AED+∠EAD+∠ADE=180°
∴∠ADE=180°-∠AED-∠EAD=180°-90°-25°=65°
5.檢查
教師指導學生細心檢查解題全過程,回顧解題步驟,重新審查推導過程,引導學生吸取有用的經驗,鞏固解題技巧,促使學生將解題結構體系搭建出來,內化解題思想和方法。
二、運用五步解題法教學要嚴把三道關
1.開口讀題是審題的關鍵
審題是解題的初始階段,要求學生能從題目中找到已知條件和所求問題,在腦海中生成初步的感知。但眾多的字母,紛繁的條件,導致學生覺得題目枯燥無味,喚不起學習興趣。那么開口讀題就顯得十分關鍵了。讀題能讓學生的注意力集中到題目上,通過眼、口、耳、手、腦的共同參與,掌握題中講的是一件什么事?弄清了題中要求的問題是什么?給了哪些條件?一旦了解了題意,解題就能逐步解決。
2.使用標記符號要精準
幾何標記符號表達的意義要清晰準確,不能再同一題目里,一種符號代表兩種或兩種以上的意思,這容易造成學生標記混亂,無所適從。特別要注意,標記符號知識輔助課堂教學的一種手段,教師在教學時切勿只標出幾個符號,卻沒有交代清楚為什么這樣標記,否則,一堂課下來,學生不會的仍然不會。
3.判斷時的引導要適時
解題教學的成功與否,很大程度上取決于啟發式提示語的運用,即一個個適時的提醒與引導。故而,教師在學生進行判斷的過程中要把握好時機,設置好引導的關鍵詞,喚醒學生已有的知識體系,讓他們在不斷的引導中順利完成思考,從中感悟解題思路和方法的生成,獲得解題經驗的積累,促使學生達到自我啟發,自我思考。
教無定法,一切教法都是為了激發學生學習數學的興趣,為了學生構建數學知識體系,為了學生提高解決數學問題的能力,為了學生累積解題的成功經驗而做準備,讓學生在潛移默化中學好數學,用好數學。

