關注倍角模型，破解中考壓軸題*
——等腰三角形中的兩個倍角關系模型在解題中的應用

☉寧夏中衛市沙坡頭區宣和鎮張洪學校 張 寧

一、模型呈現

如圖1，在△ABC中，AB=AC，BD⊥AC，垂足為D，∠BAE是頂角∠BAC的外角，則：

（1）∠BAC=2∠DBC，即等腰三角形一腰上的高與底邊的夾角等于頂角的一半；

（2）∠BAE=2∠ABC=2∠ACB，即等腰三角形頂角的外角等于一個底角的兩倍.

證明：（1）如圖2，過點A作AF⊥BC，垂足為F，則∠FAC+∠ACB=90°.

由等腰三角形“三線合一”的性質，可知AF平分∠BAC，即∠FAC=∠BAC.

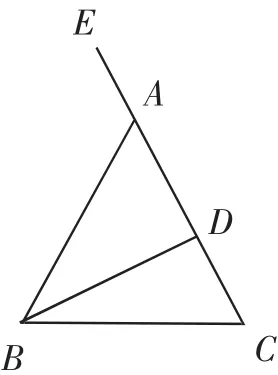
圖1

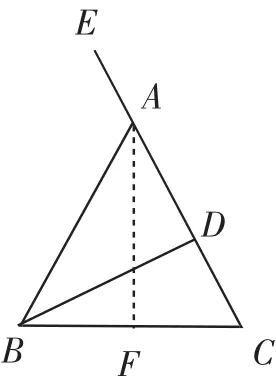
圖2

由BD⊥AC，可知∠BDC=90°，所以∠DBC+∠ACB=90°.

由“同角的余角相等”，可知∠FAC=∠DBC，所以∠DBC=∠BAC，即∠BAC=2∠DBC.

說明：圖1給出的等腰△ABC是銳角三角形，當等腰△ABC是鈍角三角形時，結論依然成立；當等腰△ABC是直角三角形時，結論顯然成立.

（2）利用等腰三角形及三角形外角的性質容易證明，此處從略.

這是等腰三角形中兩個重要的倍角關系，利用這兩個倍角關系可破解中考壓軸題.

二、模型應用

例1（2018年江蘇省揚州市）如圖3，四邊形OABC是矩形，點A的坐標為（3，0），點C的坐標為（0，6），點P從點O出發，沿OA以每秒1個單位長度的速度向點A運動，同時點Q從點A出發，沿AB以每秒2個單位長度的速度向點B運動，當點P與點A重合時運動停止.設運動的時間為t秒.

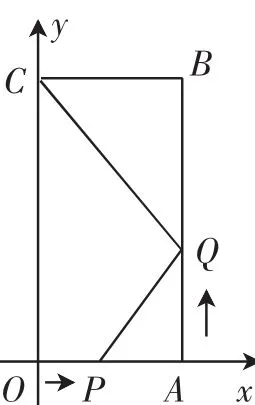
圖3

（1）當t=2時，線段PQ的中點坐標為_______.

（2）當△CBQ與△PAQ相似時，求t的值.

（3）當t=1時，拋物線y=x2+bx+c經過P、Q兩點，與y軸交于點M，拋物線的頂點為K，如圖4所示.問：該拋物線上是否存在點D，使∠MQD=∠MKQ？若存在，求出所有滿足條件的D點的坐標；若不存在，請說明理由.

解析：（1）當t=2時，OP=2，AP=1，AQ=4，所以P（2，0）、Q（3，4）.

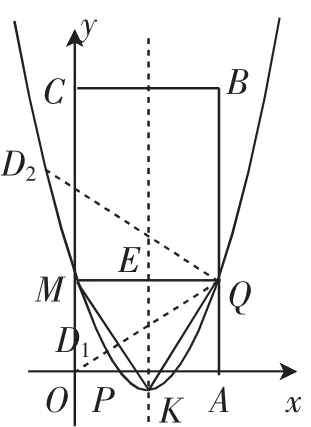
圖4

（2）由已知條件易知PA=3-t，AQ=2t，BQ=6-2t.

△CBQ與△PAQ相似有兩種情況，利用相似三角形的性質列方程易求得答案.請有興趣的讀者自行探究，限于篇幅，此處從略.

（3）當t=1時，易求得P（1，0）、Q（3，2）.將其代入y=x2+bx+c，得所以拋物線的解析式為y=x2-3x+2，從而可得點M的坐標為（0，2）.又因為Q（3，2），即點M與點Q的縱坐標相等，所以MQ∥OA.因為）是拋物線y=x2-3x+2的頂點，由二次函數的對稱性易知△KMQ是等腰三角形，KM=KQ，∠MKQ是等腰△KMQ的頂角.根據等腰三角形中的倍角關系“等腰三角形一腰上的高與底邊的夾角等于頂角的一半”，可知過點Q作KM的垂線，交拋物線于點D1，則∠MQD1=∠MKQ，如圖4所示.

如圖4，作拋物線y=x2-3x+2的對稱軸，交MQ于點E.

由等腰三角形的性質，易知∠EKQ=∠MQD1，故tan∠MQD=tan∠EKQ=.又因為MQ=3，OM=2，所以易1知直線QD1經過原點O.利用待定系數法易求得直線QD1的表達式為y=x.

如圖4，作直線QD1關于直線MQ的對稱直線，得到直線QD，點D在拋物線上.易求得直線QD的解析式為y=-x+4.222

點評：本題是函數、方程、三角形的綜合性問題，主要考查一次函數的性質、二次函數的性質、相似三角形的判定和性質、一元二次方程的解法、待定系數法等知識點，這些知識點是《義務教育數學課程標準（2011年版）》規定的最基礎、最核心的內容.本題涉及的知識點比較多，承載著較強的中考選拔性功能.本題綜合性較強，求解過程比較復雜，對學生而言具有很強的挑戰性.解決問題（2）的關鍵是用t表示出有關線段的長度，再利用相似三角形的性質即可找到相關線段之間的關系，通過列方程即可解決問題.對于問題（3），這是一個倍角或半角關系的存在性問題，解決本題的難點是將倍角關系轉化為等角關系，確定點D所在的直線，然后利用相似三角形或三角函數、一次函數、一元二次方程等知識求解.等腰三角形中的倍角關系模型在本題求解過程中發揮了重要作用，為本題的解決指引了具體的操作方向，這也是幾何模型在解決問題過程中發揮作用的基本方式.確定點D1的坐標后，根據對稱性在圖4中易作出點D2，利用相同的方法可求出點D2的坐標.從求解過程可以看出，立足基本圖形，深刻理解基本圖形的性質，對分析問題和解決問題具有非常重要的引領作用.

例2（2018年河南省）如圖5，拋物線y=ax2+6x+c交x軸于A、B兩點，交y軸于點C.直線y=x-5經過點B、C.

（1）求拋物線的解析式.

（2）過點A的直線交直線BC于點M.

①當AM⊥BC時，過拋物線上一動點P（不與點B、C重合），作直線AM的平行線交直線BC于點Q，若以點A、M、P、Q為頂點的四邊形是平行四邊形，求點P的橫坐標；

②連接AC，當直線AM與直線BC的夾角等于∠ACB的2倍時，請直接寫出點M的坐標.

解析：（1）由一次函數的性質易知點B的坐標為（5，0），點C的坐標為（0，-5）.將其代入y=ax2+6x+c，得解得所以拋物線的解析式為y=-x2+6x-5.

②如圖6，∠ACB是定角，點M在直線BC上.由已知，直線AM與直線BC的夾角等于∠ACB的2倍，則∠AMB=2∠ACB或∠AMC=2∠ACB.由等腰三角形頂角的外角與底角的關系，易知構造等腰三角形，使∠ACB是等腰三角形的底角，∠AMB或∠AMC是這個等腰三角形頂角的外角.根據圖形特征，顯然△AMC是等腰三角形，∠AMB是這個等腰三角形頂角的外角.

如圖6，作線段AC的垂直平分線，交AC于點D，交直線y=x-5于點M1，連接AM1，則△ACM1是等腰三角形.由此可知，∠AM1B=2∠ACB.以點A為等腰三角形的頂角的頂點，以AM1為等腰三角形的腰構造另一等腰三角形，落在直線BC上的頂點為M2，∠AM2C=2∠ACB.從而可知，滿足條件的點M有兩個.

如圖6，過點M1作x軸的垂線，垂足為F，過點C作直線FM1的垂線，垂足為E，過點M2作x軸的垂線，垂足為G.

易知A（1，0）、C（0，-5）.令M1（m1，m1-5）、M2（m2，m2-5），則AF=m1-1，FM1=5-m1，CE=m1，EM1=m1，GM2=5-m2，AG=m2-1.

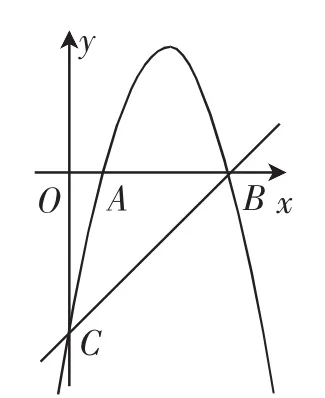
圖5

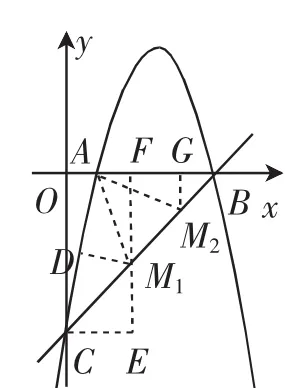
圖6

由AM1=CM1及勾股定理，可知AF2+FM12=CE2+EM12.

所以（m1-1）2+（5-m1）2=m12+m12，解得m1=，故

由AM1=AM2及勾股定理，可知AF2+FM12=AG2+GM22，

綜上所述，當直線AM與直線BC的夾角等于∠ACB的2倍時，點M的坐標為

點評：本題主要考查一次函數的性質、二次函數的性質、平行四邊形的判定和性質、一元一次方程、一元二次方程、勾股定理、等腰三角形的性質與判定等知識點.本題涉及的內容比較多，綜合性較強，求解過程比較復雜，對學生而言具有很強的挑戰性.在問題（2）中，問題①是平行四邊形的存在性問題，這是中考數學壓軸題中最常見的一類問題，解決這類問題通常需要借助平行四邊形的判定與性質，列方程求解；或借助中點坐標公式，直接利用“平行四邊形對角頂點的橫（縱）坐標之和相等”這一結論求解；問題②是倍角關系的存在性問題，根據圖形的基本特征，解決本題的難點是將問題中的倍角關系轉化為等腰三角形頂角的外角與底角之間的關系，然后借助勾股定理列方程求解.等腰三角形頂角的外角與底角之間的倍角關系模型在本題求解過程中發揮了引領作用.確定點M1的坐標后，借助對稱性或輔助圓在圖6中易作出點M2，利用相同的方法可求出點M2的坐標.

說明：由于初中學生未曾接觸平面直角坐標系內兩點之間的距離公式，所以問題②借助勾股定理列方程求解.當然，對于教師而言，本題還可以先求出直線DM1的解析式，然后聯立方程求解.

三、解題反思

1.關注基本圖形和幾何模型

圖形與幾何是初中數學中非常重要的內容，在近幾年各地中考試題中，將幾何圖形與函數圖像融合的壓軸題屢見不鮮，這類試題所涉及的知識點較多，綜合性強，對學生而言極具挑戰性.筆者認為，所有與幾何圖形有關問題的解決，幾乎都要回歸到基本圖形的性質，只有熟練掌握基本圖形的性質，深刻理解基本圖形的性質在解題中發揮作用的方式，才能得心應手地運用基本圖形解決相關數學問題，才能不斷提高學生的幾何推理能力.因此，在圖形與幾何教學中，教師要不斷引導學生建立數學模型思想.其一，不僅要讓學生熟練掌握平行線、角平分線、中線、高線、垂直平分線、等腰三角形、直角三角形、平行四邊形、矩形、菱形、正方形、等腰梯形、圓等基本幾何圖形的性質，而且要理解這些基本幾何圖形的性質在解決問題中的作用與應用方式；其二，全等三角形與相似三角形也是非常重要的幾何模型，不僅要理解它們的性質與判定，而且要學會運用它們解決實際問題；其三，要讓學生熟練掌握平移、軸對稱、中心對稱、旋轉等基本圖形變換的性質及其在解題中的作用.

2.發揮幾何模型的解題引領作用

如果學生熟練掌握基本幾何圖形的性質，內化為自身的幾何素養，在解決相關數學問題時，就能準確找到與之對應的幾何模型，然后采取行之有效的解題方法與策略，從而為考試節省不少時間.筆者認為，解決問題的過程中，雖然不宜直接利用幾何模型的相關結論，但幾何模型能夠為解題指引正確的方向，合理地使用幾何模型能使原本復雜的問題變得簡單易解，使學生少走彎路，從而提高學生分析問題和解決問題的能力.

四、結束語

《義務教育數學課程標準（2011年版）》指出，在數學課程中，應當注重發展學生的數感、符號意識、空間觀念、幾何直觀、數據分析觀念、運算能力、推理能力和模型思想.王尚志教授曾指出，學生在數學學習中應培養“數學抽象、邏輯推理、數學建模、數學運算、直觀想象、數據分析”這六大核心素養.推理能力是數學思維能力的重要組成部分，幾何推理是培養學生推理能力的重要載體.因此，幾何推理能力對學生而言至關重要.波利亞曾說過：“掌握數學就意味著善于解題.”解題是數學學習活動的基本形式，也是學生參與數學學習活動的主要內容.因此，數學學習離不開解題.波利亞在其著作《數學的發現——對解題的理解、研究和講授》中認為：“解題是一種本領，就像游泳、滑雪、彈鋼琴一樣，你只能夠靠模仿和實踐才能學到它”“中學數學教學的首要任務就在于加強解題訓練”.筆者認為，在數學學習中，教師要引導學生善于歸納總結基本幾何模型，形成模型思想，這是培養初中生幾何推理能力的有效途徑之一.