例談“實驗型”初中數學教學的實踐與反思

龔杰

[摘 要] 提升初中數學教學的實效，不能僅僅憑教師的教學經驗和滿堂灌式的教學方式，應該引導學生在活動中思考，而最佳的活動就是實驗，實驗不僅僅是理化學科教學的專項，對于數學學科同樣可以借助實驗來鍛煉學生思維的嚴謹性，同時培養學生的創造能力.

[關鍵詞] 初中數學；實驗教學

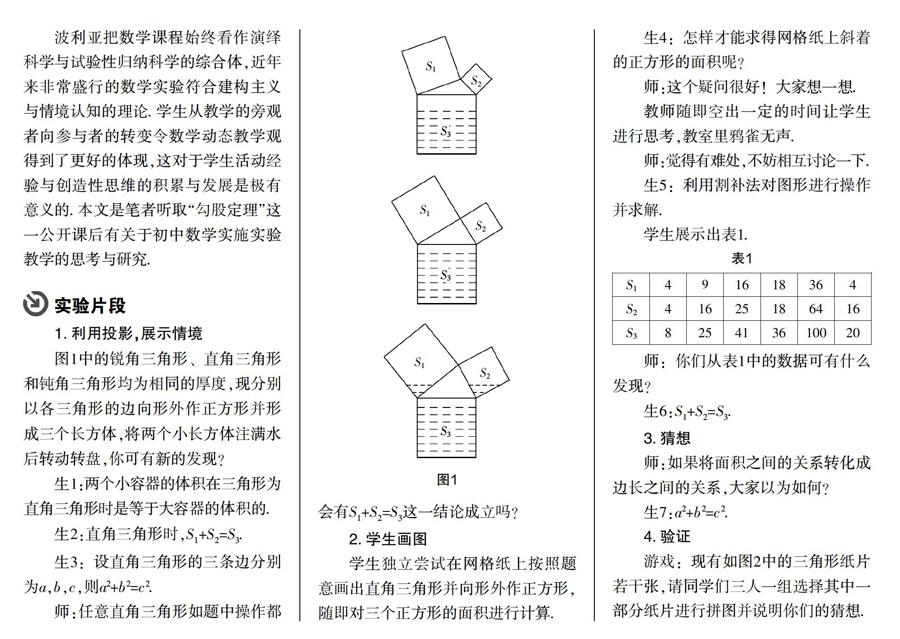
波利亞把數學課程始終看作演繹科學與試驗性歸納科學的綜合體，近年來非常盛行的數學實驗符合建構主義與情境認知的理論. 學生從教學的旁觀者向參與者的轉變令數學動態教學觀得到了更好的體現，這對于學生活動經驗與創造性思維的積累與發展是極有意義的. 本文是筆者聽取“勾股定理”這一公開課后有關于初中數學實施實驗教學的思考與研究.

實驗型初中數學教學的幾點反思

上述實驗教學的片段是針對學生的年齡特征而設計的實驗活動，“轉”“畫”“拼”三個操作性的實驗活動不僅使學生的課堂參與度大大提高，學生原有的生活經驗與數學經驗也在充分的活動、想象與嘗試中得到了最為有力的激發. 學生思維的起點因為這些操作、思考、交流而變得更有意義，學生的理性思維在其親身經歷的觀察、猜想、驗證與證明過程中得到了有效的培養. 學生合作學習的意識、習慣與精神也在小組合作學習中得到了激發與鍛煉. 最終的成果分享與成功體驗又使學生對數學學習的興趣與樂趣倍增.

筆者在這一實驗教學的課堂中仔細觀察并記錄了課堂的整個流程，筆者以為，數學實驗教學必須處理好以下五個關系才能保障其實施的有效性.

1. 處理好實驗和論證之間的關系

數學實驗雖能給學生帶來樂趣，但其最終目的并不是為了讓學生玩，而是通過一定的情境創設使學生能夠在動手操作中尋得問題解決的途徑以及問題的深入與發展. 學生能夠在探尋中獲得趣味與思索便能令其在實踐的過程中獲得數學的收獲. 那些沒有實踐的抽象論證帶給學生的往往只有空洞的理論，學生永遠無法在其中感受到數學學習的生命力.

本課勾股定理的實驗教學從空間形式與數量關系兩個方面進行了科學的情境創設，學生在“體積——面積——三角形邊長——直角——三邊關系”的猜想、實驗與論證中進行了充分的思考也收獲了成功的喜悅. 拼成圖形的過程以及論證也使學生在經歷、體驗、感悟數學活動的過程中牢固地掌握了勾股定理的相關推理與知識，這是一個實驗教學運用于數學課堂教學的示范案例.

2. 處理好證實和證明的關系

通過情境與實驗的設計引導學生在觀察、實驗、探索、驗證中獲得數學知識并探求猜想的正確性，學生的合情推理能力在親身經歷中得到了很好的鍛煉與發展. 不過，止步于此仍是不夠的，教師又根據學生年齡特征設計了不同程度的問題，令學生在演繹推理中不斷交流、合作并最終提煉出一般規律，學生運用準確的語言對實驗過程進行表述又令其表達能力得到了提升. 學生在教師所設計的勾股定理的實驗教學中通過畫圖證實了所有直角三角形都滿足a2+b2=c2的結論，并在后續的拼圖與驗證中鍛煉了合作學習與嚴密思維的能力，可以說，實驗教學在本課教學的運用是相當成功的.

3. 處理好預設和生成之間的關系

好的數學實驗的設計與開展不僅能夠貼合學生的最近發展區，而且能夠在充分調動學生參與度的同時在課堂上產生新的生成. 那些完全按照教師預設的風平浪靜的課堂要么學生的積極性沒有得到很好的調動，要么這只是一場虛假的表演罷了.

學生在本課實驗教學的設計中拼出了很多教師都沒有意料到的圖形，這雖然與教師的預設不盡相同，但卻表現出了學生思維的積極狀態. 教師如果對新的生成不能很好地處理，那么，學生的思維就會受到極大的限制.

比如，教師在學生提出直角三角形中a2+b2=c2的結論時不予理睬，還是按照自己原先設計的探求S之間的關系來進行自己的教學，學生的思維就會被中途打斷而影響其學習的效果. 因此，教師面對課堂教學中新的生成應及時把握并因勢利導，使學生的思考與創新得到及時的保護與肯定，教學活動因為教師的適時調整一定會取得更好的效果.

4. 處理好活動經驗積累與數學思維拓展之間的關系

數學活動的經驗只有在不斷的“思考”和“做”的過程中才能得到逐步的積累與沉淀. 蘊含在數學知識形成、發展以及應用過程中的數學思想是數學知識的抽象與概括，因此，數學實驗教學的設計與開展應在考慮學生年齡特征的基礎上注重活動經驗的積累以及數學思想的拓展，顯性知識的學習與隱性知識的滲透在實驗活動中缺一不可.

一般來說，具備具體知識點的顯性知識應該在實踐、探索以及交流講解中完成，而沒有明確知識點的隱性知識則應該在經歷和體驗中接受. 學生在本課勾股定理的學習中經歷了“轉”“畫”“拼”等實踐過程并因此體驗到了勾股定理證明的必要性以及方法的多樣性，深化、發展問題的同時也使學生思維的嚴密性與靈活性得到了有效的培養.

5. 處理好實驗和非實驗之間的關系

數學實驗的設計與開展使學生在玩中充分體驗數學的趣味性與價值，學生學習數學的方式也會因此得到更大的轉變，師生之間的距離以及學生與數學之間的距離因為實驗活動的設計與開展也被大大縮短，這對于數學活動經驗的積累以及創新思維的培養大有裨益. 不過，教師也應該清楚認識到并非一切數學學習都需要通過實驗的開展來進行，教師應該根據具體的教學內容選擇實驗、演繹推理、講解等各種方式進行針對性的教學. 比如，本課勾股定理的實驗教學中就包含了實驗、討論、交流等多種學習方式，拼圖、推理等動手動腦的活動使得勾股定理的文化感受與應用得到了很好的展現. 當然，教師的主導作用并不會因為實驗活動的開展而削弱，沒有討論與交流的單純實驗是遠遠不夠的，實驗活動與探索交流相互融合的活動才能使學生真正經歷知識的感知、理解、意會、表達、抽象以及證明等過程，并使所學內容內化為學生自己能夠掌握和應用的知識.