“商的變化規律”教法新探

廣西上林縣大豐鎮中心學校(530500)

羅惠芳

教學“商的變化規律”這一內容時，學生雖然易于理解“除數不變時，商隨被除數同時變化”，但是對“被除數不變時，商與除數反向變化”的理解就有了困難。同時，學生雖能容易背記商的不變規律，但不理解商的不變規律與商的變化規律之間有什么關系。為了突破這一教學難點，課堂教學中，教師先讓學生根據自己已有的知識經驗進行探究，再將商的不變規律和變化規律有機融合，使之貫穿于整個教學始終。

一、引入生活，初步感知規律

投影儀顯示：圣誕節給福利院的小朋友分發一箱熒光棒，每人分到4支熒光棒。

師：“每人分到4支熒光棒”，怎么列出文字表達式？

生1：一箱熒光棒數÷福利院孤兒數=4(支)。

師：文字表達式中的“一箱熒光棒數”，在除法算式中屬于什么數？

生：被除數。

師：那“福利院孤兒數”和“4支”又代表什么數？

生：除數和商。(師板書：被除數÷除數=商)

投影儀顯示：如果每箱的熒光棒數都相同，武昌區每個福利院的孤兒數都相同，你能快速算出下面三題嗎？

①把兩箱熒光棒平分給一個福利院的孤兒，每人分得( )支。

②把一箱熒光棒平分給兩個福利院的孤兒，每人分得( )支。

③把兩箱熒光棒平分給兩個福利院的孤兒，每人分得( )支。

師：請大家先通讀題目，綜合考慮前后條件的變化，再思考分得的結果不同是什么原因造成的。(生分組探究后，師組織反饋匯報)

生2：因為原題只有一箱熒光棒，而第①題變為兩箱熒光棒，總數增加一倍，于是每人分得的熒光棒增加一倍。

師：那第③題也是兩箱熒光棒，為什么每人分得的還是和原來一樣多？

生3：因為要分給兩個福利院的孤兒，熒光棒的數量雖然增加一倍，但是孤兒的數量也增加了一倍。

師：在第①題中，熒光棒的數量增加了幾倍？

生：2倍。

師：也就是說，除法算式里的被除數增大了2倍。

師：第①題中的孤兒數沒變，對應除法算式中就是除數沒變。

師：我們根據實際情況進行合情推理，得出每個孤兒分到熒光棒的數量比原來多了一倍，也就是說除法算式中的商擴大了2倍。[板書：(被除數×2)÷除數=(商×2)]

[然后師用同樣的方法引導學生總結得出：(被除數×2)÷(除數×2)=商(不變)，被除數÷(除數×2)=(商÷2)]

師：請大家觀察商的變化規律的公式，思考一下，商的不變規律與變化規律有關系嗎？

生4：有關系。被除數增大2倍，引起商增大2倍；除數增大2倍，引起商縮小2倍。當被除數和除數同時增大2倍時，它們對商的牽連作用相抵消。

……

然后教師讓學生結合前面的結論，繼續觀察算式并思考探究。

二、明晰結構，學會借助生活經驗

一般來說，學習者的學習起點分為兩部分：一是認知結構的根基起點和客觀的生活起點。從上述教學中不難看出，教師對學生學習起點的把握比較到位，不僅注重學生認知結構的根基起點，而且對學生客觀的生活起點更加重視。從教學效果來看，學生能根據生活情境進行合情推理與想象，憑借敏銳的直覺準確地推知每一題的結果，分析出熒光棒數量與福利院孤兒數之間的關系。另外，在引導學生質疑時，教師及時引導他們把生活中的分配經驗用除法算式表示出來，使學生清晰地感知被除數、除數和商之間的變化關系。然后教師又特意讓學生對這些關系進行整體觀察、思考，使學生從邏輯上認可和理解商不變的根本原因——被除數的牽連變化與除數的牽連變化相互抵消。這樣教學，使學生初步理解了不變與變化的辯證關系，為接下來的學習打好基礎。

三、倡導自學，學會統領全局

1.引導自學

師：剛才大家理解了被除數和除數單獨或同時增大2倍時商的變化規律，那么當擴大的倍數變為任意數時，這個規律是不是還存在？請大家帶著問題自學。

投影出示：

①計算課本P87中例8的各組算式。

②想辦法結合算式解釋變化規律。

③舉出不同的例子來驗證你所發現的規律。

④小組交流自己的發現。

2.小組交流

學生匯報計算結果，師抽查學生對規律的解釋情況并舉例。講解第一條規律時，師出示下圖，讓學生結合具體算式進行解釋并舉例。

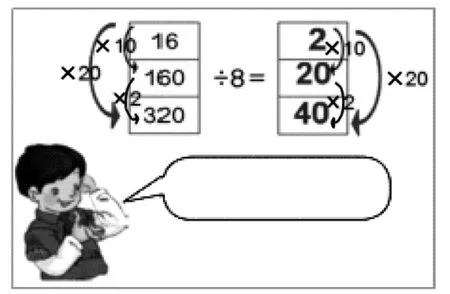
生5：與原題相比，第二道算式中的被除數乘10，除數仍為原數，商也乘10。

生6：與原題相比，第三道算式中的被除數乘20，除數仍為原數，商也乘20。

……

師隨機抽取學生列舉的兩組題：

24÷6=4 12÷4=3

240÷6=40 48÷4=12

48÷6=8 120÷4=30

師讓學生根據自己的舉例，再次驗證第一條規律。隨著學生解析題意，師及時地將表述語句中的“×2”更換成“×幾”。在學生闡釋第二條規律時，師出示下圖，讓學生說算理。

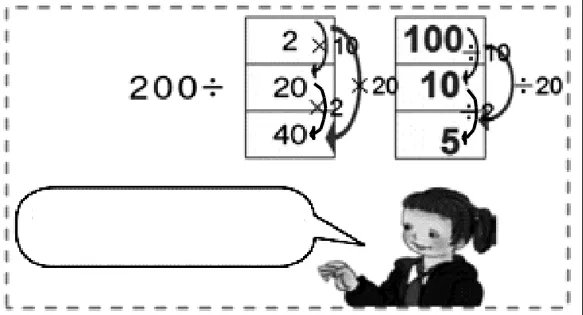
對于第(3)組的算式和規律，教師繼續讓學生解讀，學生在獨立思考和小組研究后進行匯報展示。集體交流中，教師引導學生重點對商的不變規律進行研討。有學生提出“商不變是因為被除數和除數引起反向的變化作用相互抵消造成的”，教師順勢強調“這三條規律是互通的，只要記住第三條規律就可以推導出前兩條規律”……

上述教學，在學生初步掌握規律的前提下，教師引導學生帶著探究的目的和欲望進行自學。課本在每組算式后都指明了規律，所以學生只要計算出結果，再進行特征觀察和概括后就能總結出規律。為了讓學生深入理解規律，教師要求學生根據規律寫算式，再由結論擴展至創編算式，培養學生的逆向思維。

總之，數學課堂中，教師只有引導學生學會概括總結、舉例驗證、反思交流，不斷深入探究和分析，才能有效規避分步教學的弊端，使學生真正理解和掌握所學知識。