關注學生起點，優化教學設計

☉江蘇省宜興市和橋高級中學 張 菁

☉江蘇省宜興市和橋高級中學 杜 健

建構主義將學習視為新舊知識與經驗互相作用而造成的認知結構重組，任何一種知識與技能的學習都應該建立在已有知識與技能的基礎之上才能獲得發展.因此，教師在實際教學中應著眼于學生的知識起點與能力水平為學生設計出適合學生發展的教學活動，只有準確定位學生的起點狀態所設計的針對性教學才能使學生體驗到“跳一跳，夠得到”的成功體驗.

一、基于學生已有經驗創造情境

案例1 直線的斜率（教學片斷）.

教師首先在直角坐標系中作出一條直線并提問：大家能在老師所畫圖形中知道哪些呢？學生在一定的思考、聯想與討論以及教師的啟發后獲得“一次函數的圖像”這一答案.

師：大家知道這是哪種一次函數嗎？這說明了什么呢？

生：兩點確定一條直線.

師：大家想想還有其他方法能夠確定直線的嗎？

（投影蹺蹺板）

師：這是大家都玩過的游戲，大家觀察一下蹺蹺板的運動過程可有什么發現？蹺蹺板運動時形成的諸多直線可有什么共同的特點呢？

生：它們是經過同一個點的.

師：很好，不過這些直線當中卻沒有任何一條是確定下來的，如果給它一個方向是不是就可以確定了呢？

生：對.

師：我們一般用坐標來確定點的位置，大家可曾想過方向又可以用什么來表達呢？斜拉橋是大家都有概念的，斜拉橋上的諸多直線對于橋面而言分別存在著不同的傾斜程度，這些傾斜程度又該怎么表達呢？

學生結合預習所得與討論得出了坡度這一概念.

師：坡度是如何確定的？假如給你任意兩條直線，對其傾斜程度應如何判斷呢？

生：將其置于直角坐標系中進行判斷.

師：很好，研究幾何圖形問題時常會運用到代數方法.請大家看一下直線AB并思考問題：假如將直線上的兩點用坐標刻畫，大家能用這兩點的坐標來刻畫出直線AB的傾斜度嗎？

師：這就是我們今天所要學習的內容——直線的斜率.

本案例著眼于學生的已有知識經驗以及生活經驗引出“怎樣確定直線的方向”這一問題，學生的認知沖突形成并在直觀感受中對問題展開探索，建立在學生認知起點所設計的教學過程也更加自然.

二、基于學生知識水平組織教學

案例2 曲線的參數方程（教學片斷）.

師：摩天輪是大家都熟悉的吧？如果某游樂場的摩天輪的半徑是60米，摩天輪逆時針勻速旋轉的速度是弧度/秒，如圖1，小明現在點P0處，則t秒后小明會在何處呢？大家可以討論一下，這一問題應該如何解決呢？

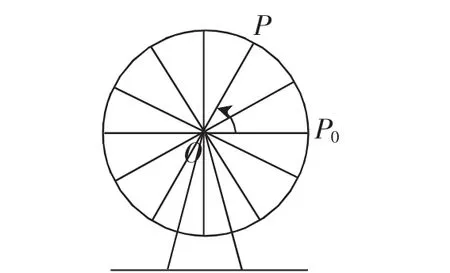
圖1

生：設小明在t秒后會在點P（x，y）處，則

師：很好，建立點P的坐標能夠很好地描述小明在不同時刻所處的位置.大家可曾想過：時間不同，小明所處的位置也是不同的，這所有不同的位置會不會形成一個軌跡呢？

生：會，是一個圓，圓的方程為x2+y2=3600.

師：上述關系式是否可以作為圓的方程呢？理由如何？

生：能，利用曲線方程的定義可以對此進行證明.

師：圓的方程包含標準式與一般式兩種形式，上述方程是何種形式？它應該有一個什么樣的名字呢？

生：參數方程.

師：很好，這就是我們今天的研究課題.圓是我們所熟悉的，假如某圓的圓心在原點，半徑是r，大家能寫出它的方程嗎？它的參數方程又是怎樣的呢？

師：如何說明這一參數方程確實表示的是圓x2+y2=r2呢？

生：消去參數即可.

師：好！那么，假如圓的方程是（x-a）2+（y-b）2=r2，參數方程是什么呢？

教師在這一內容的教學中并沒有機械地按照教材內容的安排組織教學，而是根據學生已經掌握的曲線普通方程、求曲線普通方程的方法、比較常見曲線的幾何性質等知識引導學生進行了對比與類比，教師幫助學生在熟悉的曲線上逐步體會到了建立曲線參數方程的方法，這種以學生發展為本的教學設計往往能取得很好的教學效果.

三、基于學生困惑組織教學

案例3 等差數列的錯解評析（教學片斷）.

投影問題：在等差數列{an}與{bn}中，Sn與Tn分別為其

師：此題從不同角度考慮可得出不同解法，看看大家能得出哪些解法呢？

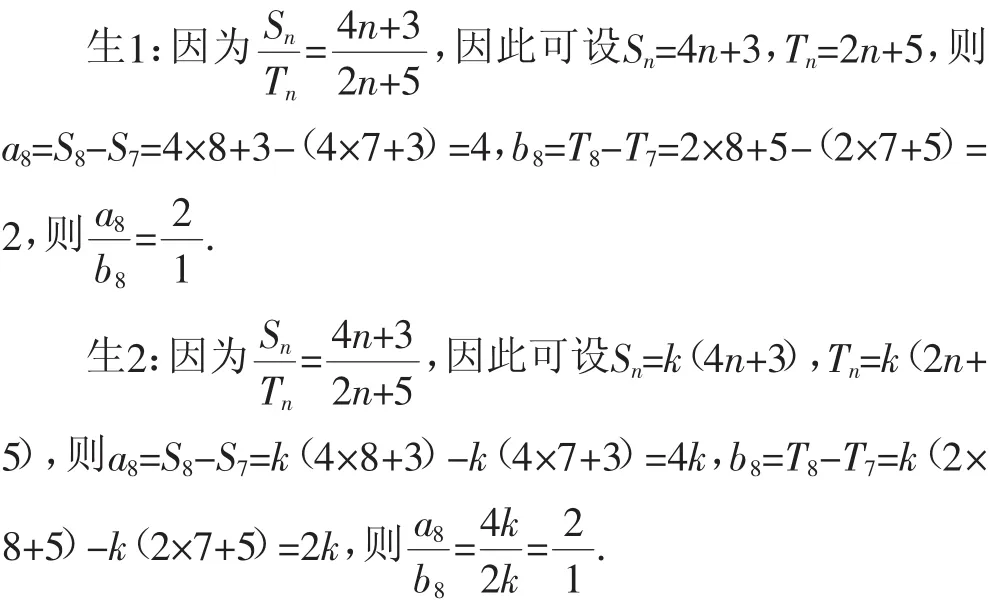
師：兩位同學的解法雖然各異，但最終結果卻是一樣的，大家以為他們的解法如何？生3：生1的解法不對，不過結論是對的：因為由并不能得到Sn=4n+3，Tn=2n+5，生2的解法沒有錯.

師：大家可有其他想法？

生4：生2的解法也是錯的.設Sn=k（4n+3），Tn=k（2n+5），表明數列{an}與{bn}的前n項和都為n的一次式，但假如等差數列不是常數列，它的前n項和Sn為形如an2+bn的二次式，所以，應設Sn=k（4n+3），Tn=k（2n+5），則可得到a8=S8-S7=k·8（4×8+3）-k·7（4×7+3）=63k，b8=T8-T7=

師：很好，指出了他們的錯誤，還給出了正解.由Sn=可知，當等差數列為常數列時才能把其前n項和設成Sn=an+b這一形式，但這一條件在此題中并不存在，兩位同學這是對等差數列的前n項和公式的特征認識不夠而導致了錯誤的產生.大家想想看這一問題還有其他的方法可解嗎？

案例3的教學過程中，教師并沒有讓學生陷入題海中操練，也沒有進行大量重復的講解，而是設計了一個典型的問題將學生引入了探究與思考中，對學生思維的困惑與障礙進行及時的捕捉并引導學生在錯誤解法上展開討論，將課堂生成的鮮活資源進行了很好的利用并引導學生對錯誤根源進行了探索，引導學生在認知沖突上進行質疑、探究、思考并獲得省悟，學生在得到充分尊重的心理滿足中也對學習產生了更加積極的態度，學生認知結構得到提升的同時也令學生的智力與能力得到了發展.

由此可見，從學生的生活經驗與已有知識出發進行有效的數學教學能夠為學生創造出更多實踐活動與交流的機會，學生在親身經歷知識的探索中才能對所學形成更好的理解，因此，教師應摸清學生的知識狀況并基于學生的知識基礎、生活經驗、認知規律與心理特征進行教學的精心設計，準確定位教學的起點并設計出能夠突出教學重點的方案，使學生能夠在成長點上進行思考與探索并獲得教學難點的突破.學生在學習過程中探索、構建、完善認知結構的過程正是學生智力、能力快速成長的過程.學生在數學學習中獲得了多少的理解與感悟往往受其知識背景、生活經驗等因素的影響.教師采取怎樣的方式進行教學取決于教師如何看待學生在學習中的需求.教師只有準確把握學生的學習起點與學習需求并進行有意義的教學設計，才能將學生已有的知識經驗發揮出最大的功效并最終獲得理想的課堂教學效果.W