基于CS-Jounce模型的船搖濾波與預報方法

戴正旭,杜昌平,鄭 耀,陳嘉鴻

(1.浙江大學航空航天學院,浙江 杭州 310027;2.中國衛星海上測控部,江蘇 江陰 214431)

0 引 言

海上動平臺測量需要獲取船舶姿態數據,進行姿態修正后才能得到準確的目標位置信息[1],對實測船搖數據濾波去噪能提高測量數據精度。跟蹤目標時,為了提高跟蹤精度,克服高動態工況下動態滯后誤差較大的問題,需要計算前饋值,輸入天線伺服跟蹤環路[2],此時需要計算船搖數據角度量、角速度量及角加速度量的預報值。故研究船搖數據特性及其濾波和預報方法,對提高海上綜合測量精度有較強的意義。

根據工程應用需求,船搖數據實時濾波及預報需滿足以下要求:①數據積累過程短,達到滿足工作條件的積累點數盡量少;②計算量較小,能滿足實時計算的要求;③能同時適用于橫搖、縱搖、艏搖的數據濾波及預報;④能同時給出船搖角度數據、角速度及角加速度數據的濾波及預測值;⑤預報精度盡可能高;⑥魯棒性較好,不易受野值影響。

國內外針對船舶姿態預報的研究成果很多,長自回歸(autoregressive,AR)模型[3]在確定階數的條件下精度滿足要求,但有積累點數較多、不同海況或船舶工況下需調整參數的問題;卡爾曼濾波在船搖預報中的研究目前大多基于船舶水動力學模型[4-9],缺點是建模復雜,風浪的影響無法準確建模,且一旦動力學參數發生變化時,也會導致濾波精度下降;基于神經網絡的方法[10-13]具有較高的預報精度,但只針對橫搖數據進行研究,對艏搖和縱搖數據適用情況未有涉及。基于信號分解和AR模型綜合預報的方法[14]提高了船搖預報時長,但實時性能不能滿足要求。此外以上所有方法均未涉及船搖數據的濾波問題,以及船搖角速度和角加速度的估計和預報問題。

文中將基于船搖數據特性分析,引入機動目標跟蹤理論,提出基于最大相關熵的自適應“當前”統計Jounce模型(“current” statistical Jounce model,CS-Jounce),改進及創新點包括:①針對目前Jerk模型階數不夠的問題,推導了更高一階的Jounce模型;②結合自適應方法和最大相關熵理論,提高了模型的跟蹤穩定性和魯棒性;③無需對數據進行特殊預處理,同時適用于船舶的橫搖、縱搖及航向數據預報;④可同時解決船搖數據的濾波、預報及角速度、角加速度的估計和預報問題。

1 船搖數據特性分析

文中基于某測量船姿態數據進行分析,3級海況,采樣頻率20 Hz,數據點數8 000點,時長400 s,包括橫搖、縱搖和航向。

1.1 時域分析

對信號的傳統分析方法是波形分析,信號的特性首先表現為它的時間特性。從原始數據圖(見圖1)可以看出,船搖數據具有明顯的非平穩性和周期性,橫搖和縱搖數據均值在零附近,航向數據均值可能較大,且由于船舶航行中可能改變航向,除有局部短周期外還可能有長趨勢非周期項。

圖1 原始船搖數據Fig.1 Raw ship-swaying data

1.2 頻域分析

圖2給出了船搖數據的頻譜特性分析圖,因航向數據均值非零,低頻部分均出現了峰值,掩蓋了其他頻譜特征部分,對此文中采用一次差分的方法消除低頻特征后再研究(見圖2(d))。從圖2中可以看出,船搖數據均存在明顯的頻率峰值,但非單峰分布,橫搖、縱搖、航向數據頻譜分布帶相似,集中在小于0.6 Hz的低頻波段。

圖2 船搖數據頻譜特性圖Fig.2 Spectrum of ship-swaying data

1.3 噪聲特性分析

常用的測量數據噪聲分析方法有時域、頻域及時頻分析方法。

時域分析中常用的有變量差分法和最小二乘擬合殘差法[15]。但兩者都有局限性:變量差分法對于隨機誤差序列非白噪聲的數據統計結果會失真;最小二乘擬合殘差法在未加權情況下統計結果容易受到野值的影響,且擬合使用的數據點數及多項式階數確定比較繁瑣。

基于頻域的濾波分析法,是基于傅里葉變換,將有用信號和噪聲信號在頻域進行分離,從而達到去噪的效果,缺陷在于,實際情況噪聲頻譜幾乎都是分布在整個頻域內,進行噪聲平滑的同時,也必定平滑了非平穩信號的突變點。時頻分析中的小波方法能克服頻域濾波的缺點,但實際應用中需綜合權衡分解階數、閾值及小波核的選取。考慮到船搖數據基于船舶自身的慣性,不存在很多突變點,文中采用低通濾波的方法分離并分析船搖數據噪聲。

設計巴特沃斯低通濾波器,通帶截止頻率0.6 Hz,阻帶截止頻率4 Hz,表1給出了各數據噪聲均方差統計結果,圖3分析了隨機誤差特性,其頻譜圖非均勻分布,具有隱周期成分,故船搖數據環境非高斯白噪聲。

表1 船搖數據噪聲均方差統計結果Table 1 Statistical results of the mean variance of ship-swaying data noise

圖3 噪聲頻譜特性圖Fig.3 Noise spectrum diagram

1.4 船搖數據高階量分析

去除噪聲后船搖數據高階量信息可以通過差分的方法獲得。圖4橫搖為例,繪制了濾波后數據的一階至四階差分曲線圖。

圖4 橫搖高階數據示意圖Fig.4 High order data of rolling data

從圖4中可以看出,船搖數據四階差分前一直具有明顯的周期性,對這樣的數據使用Jerk模型明顯階數不足。四次差分后加加加速度量(jounce)周期性顯著減弱,故船搖過程可以看成是jounce噪聲量驅動過程。同時需注意到個別段落存在jounce量振蕩加劇的現象。

表2給出了船搖數據Jounce量的統計結果。

表2 船搖數據jounce統計結果Table 2 Statistical results of ship-swaying data jounce

2 CS-Jounce模型

第1節分析指出船搖數據具有以下特征:

(1) 數據環境非高斯白噪聲;

(2) 可以看成是jounce噪聲量驅動過程,同時必須考慮個別時間段jounce振蕩加劇的現象。

故做短時間預報時,可將船搖數據看作連續機動的過程,避免復雜的船舶姿態動力學建模。

常用的目標機動模型有[16]:勻速直線運動模型,勻加速直線運動模型,一階時間相關模型,增加階數的時間相關模型(Jerk)[17],“當前”統計模型等。在此基礎上有文獻[18]借鑒“當前”統計思想,提出了CS-Jerk模型。文獻[19]分析了Jerk模型的缺陷,指出其跟蹤高動態目標時穩態誤差不為零,證明CS-Jerk可克服此問題。

從船搖數據特性可以看出使用Jerk算法仍有階數不足的問題,故文中基于CS-Jerk模型思路,增加一階,提出CS-Jounce模型。

2.1 CS-Jounce模型

船搖數據jounce量可認為服從非零均值的時間相關過程,將jounce上一時刻的一步預報值作為當前時刻jounce的均值,運動模型為

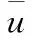
目標的連續系統狀態方程為

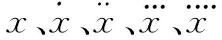
將連續方程離散化后得目標的離散系統狀態方程為

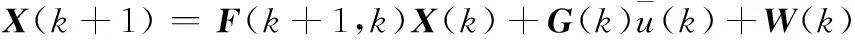
量測方程為

Z(k)=H(k)X(k)+V(k)

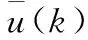
當采樣周期為T時,狀態轉移矩陣為

其中

T=tk+1|-tk

o1=(6e-αT-6+6αT-3α2T2+α3T3)/(6α4)

p1=(2-2αT+α2T2-2e-αT)/(2α3)

q1=(e-αT-1+αT)/α2

r1=(1-e-αT)/α

s1=-e-αT

當αT足夠小時,矩陣退化為

其中

q11=(18+36αT-36α2T2+24α3T3-12α4T4+

21α5T5/5-α6T6+α7T7/7-72αTe-αT-

12α3T3e-αT-18e-2αT)/36α9

q12=q21=(6-12αT+12α2T2-8α3T3+7α4T4/2-

α5T5+α6T6/6-12e-αT+12αTe-αT-

6α2T2e-αT+2α3T3e-αT+6e-2αT)/12a8

q13=q31=(3+6αT-6α2T2+3α3T3-α4T4+

α5T5/5-12αTe-αT-α3T3e-αT-3e-2αT)/6α7

q14=q41=(3-6αT+3α2T2-α3T3+α4T4/4-

6e-αT+6αTe-αT+α3T3e-αT+3e-2αT)/6α6

q15=q51=(3-6αTe-αT-α3T3e-αT-3e-2αT)/6α5

q22=(-3+2αT-2α2T2+4α3T3/3-α4T4/2+

α5T5/10+4e-αT+2α2T2e-αT-e-2αT)/2α7

q23=q32=(1-2αT+2α2T2-α3T3+α4T4/4-

2e-αT+2αTe-αT-α2T2e-αT+e-2αT)/2α6

q24=q42=(-3+2αT-α2T2+α3T3/3+4e-αT+

α2T2e-αT-e-2αT)/2α5

q25=q52=(1-2e-αT-α2T2e-αT+e-2αT)/2α4

q33=(1+2αT-2α2T2+2α3T3/3-4αTe-αT-e-2αT)/2a5

q34=q43=(1-2αT+α2T2-2e-αT+

2αTe-αT+e-2αT)/2α4

q35=q53=(1-2αTe-αT-e-2αT)/(2α3)

q44=(-3+2αT+4e-αT-e-2αT)/2α3

q45=q54=(1-2e-αT+e-2αT)/2α2

q55=(1-e-2αT)/2α

當αT足夠小時,Q(k)退化為

Q(k)=

jounce的預測方差為

假設umax為最大機動jounce量,則jounce方差為

2.2 jounce自適應模型設計

CS模型缺點在于對目標機動頻率、目標機動最大加速度兩個參數依賴性較高。針對目標機動最大加速度自適應問題有很多改進方法,函數模糊隸屬函數[20-23]是自適應調整中采用比較多。但相比于階躍特征的信號,船舶姿態運動jounce量是在最大值范圍內繞零值上下波動的,按CS自適應理論,處于零值附近時目標機動范圍可能性更廣,對應方差應該最大,但若按上述論文思路,將每個時刻的Jounce值都調整到[(4-π)umax/4,umax]或[u-max,(4-π)u-max/4]范圍內顯然是不可行的。

文中需要解決的問題是當船搖jounce量出現短時劇烈震蕩時,其范圍可能超出事前統計最大值umaxt,此時需要動態調整umax。以下借用高斯函數模糊隸屬函數思想設計函數,原則為,設計最大安全機動范圍uth>umaxt,正常情況下計算值umax≈umaxt,當u>umaxt時,動態計算保證umax>u的公式為

M函數借助了以uth為中心,δ為方差的正態分布函數,μ值保證1-μ≤M≤1,從而控制umax計算最小值。

根據表2中橫搖jounce量的統計特性可知:umaxt=0.818,設計參數,δ=1.5,uth=4,μ=0.8。從隸屬函數圖5中可以看出,-1≤u≤1時umax變化平緩,|u|≥1時,umax能迅速調整適應更劇烈的機動狀態。

圖5 隸屬函數示意圖Fig.5 Membership function

3 最大相關熵卡爾曼濾波器

實際的船搖數據在數據的收集、傳輸或處理過程中經常受到一些隨機誤差的影響,產生各種噪音,它們極少服從正態分布,有的幅值較大,還有的是奇異點。

卡爾曼濾波器為基于最小方差理論針對線性系統的狀態估計方法,因其實現簡單且在高斯環境下獲得最優解,在現實中被大量應用。但當系統環境非高斯白噪聲時,濾波效果會變差[24],尤其數據含脈沖性質的噪聲影響時,系統的魯棒性欠佳。

針對非高斯白噪聲系統的狀態估計,常用方法有狀態擴展、量測差分[25]。但對于重尾分布的噪聲,很難基于一步相關模型去描述,同時也需要比較大的計算量,很難在實時應用。多模型方法[26]也是針對非高斯白噪聲系統的手段,但主要缺點是多個模型并行運行,計算量較大。

最大相關熵準則(maximum correntropy criterion,MCC)作為非高斯信號處理的最佳魯棒準則,近年來已成功應用于自適應濾波領域[27-28]。文獻[29]結合最大相關熵準則和不動點迭代算法,提出了最大相關熵卡爾曼濾波器(maximum correntropy Kalman filter,MCKF)。理論和實踐均表明,該濾波器對非高斯噪聲具有良好的魯棒性。

文中結合“當前”概率模型,總結算法流程概況如下:

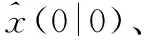
步驟2根據狀態預測和方差預測獲得一步預報值，即

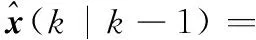
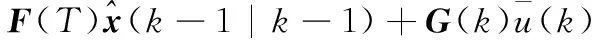
P(k|k-1)=

F(T)P(k-1|k-1)FT(k-1)+Q(k-1)

計算P(k|k-1)的Cholesky分解獲得Bp(k|k-1);計算觀測噪聲陣R的Cholesky分解獲得Br(k)。

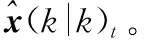
(1)

其中

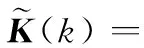
(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

(12)

步驟5比對當前狀態估計量和步驟4迭代狀態量,若滿足(13)式的迭代收斂條件則終止迭代,進行步驟6,否則t+1→t,繼續步驟4迭代計算。

(13)

步驟6更新最終方差陣,k+1→k,回到步驟2 進行下一點計算。

4 結果分析

4.1 參數設置

文中方法使用參數設置及原則如下:

(1) 目標機動常數的倒數α。根據表2中jounce頻率分布范圍,α取值范圍為0.5～10,結果差別不大,根據頻譜特征最集中段,分析時使用α=3。

(2) 觀測噪聲R。根據表1中噪聲統計結果可設對應的觀測噪聲量。

(3) jounce機動最大值自適應參數。詳見第2.2節。

(4) 相關熵參數設置。包括核函數帶寬σ和迭代收斂條件ε。文獻[29]中指出,對于非脈沖噪聲,σ選取決定其性能是否能超過普通卡爾曼濾波器。以下分析時,綜合考慮效果和性能,選擇σ=3,ε=10-6。

4.2 實際效果

衡量濾波結果好壞的指標通常有均方根誤差和平滑度,其中平滑度可以限制過擬合,但對于船搖數據平滑度指標設置比較困難,預測誤差也可以反映模型準確度,限制過擬合,故文中結合濾波均方根誤差和三步預測誤差值的均方根誤差綜合考量。

圖6以橫搖數據為例給出了濾波效果,表3給出了濾波和預報誤差統計結果。

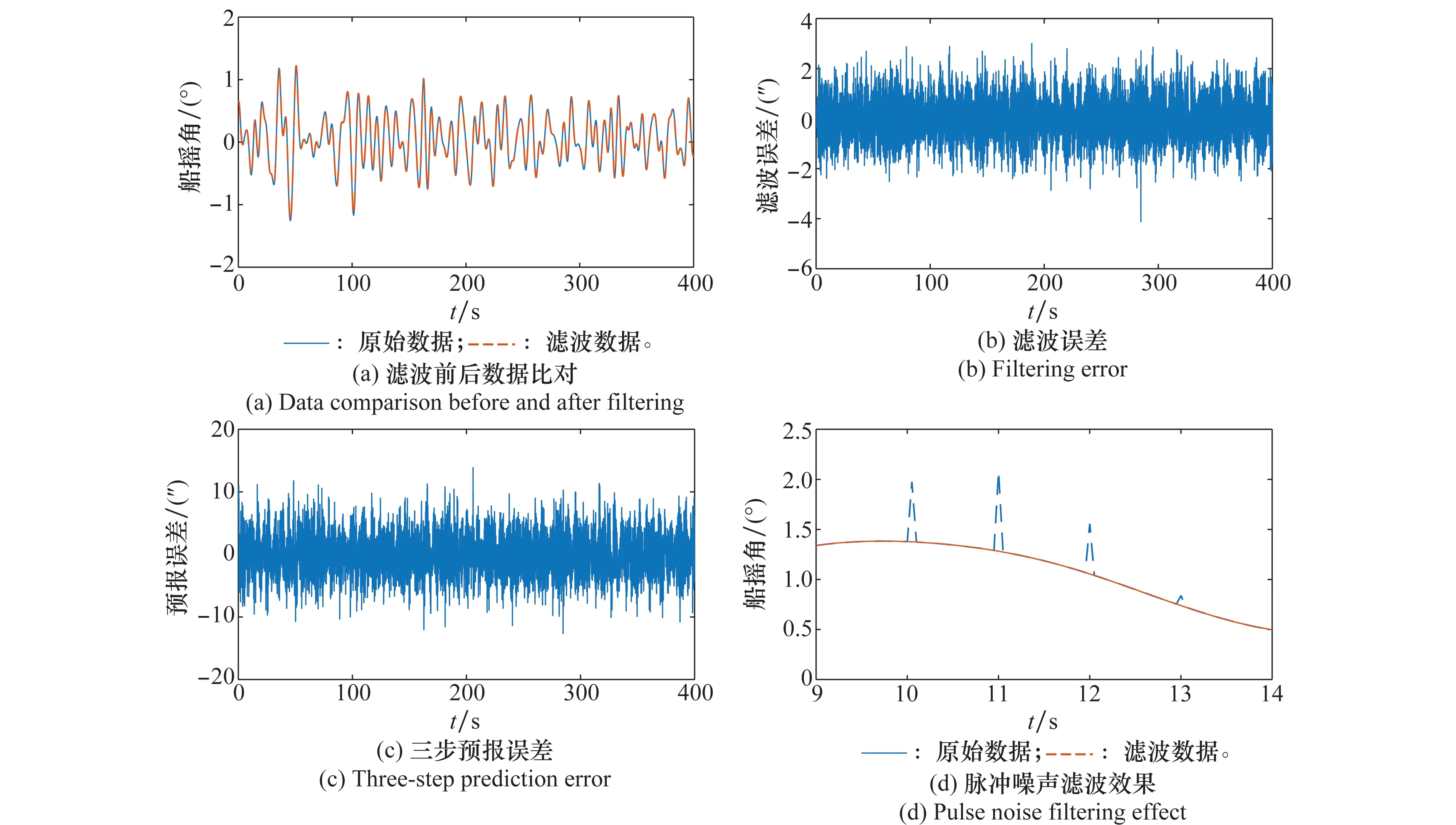
圖6 橫搖數據濾波及預報效果圖Fig.6 Filtering and forecasting effect of rolling data

表3 濾波及三步預報誤差均方根Table 3 Mean square error of filter and three-step prediction

可以得出以下結論:

(1) 該算法能很好地跟蹤船搖數據,濾波誤差中不存在明顯趨勢量;濾波后數據平滑度較高,能有效濾除船搖數據噪聲。

(2) 濾波誤差統計結果與表1分析結果一致性較好。

(3) 表3的三步預報誤差統計結果表明,該算法能實現船搖數據的準確預報,均方根誤差小于5″。

(4) 表3的統計結果表明,該方法能準確預報船搖角速度及角加速度,角速度預報均方根誤差約為0.006(°)/s,角加速度預報均方根誤差小于0.4(°)/s2。

(5) 圖6(d)表明,該方法魯棒性較好,尤其針對脈沖噪聲數據,不會出現普通卡爾曼濾波器的精度變差的現象。

5 結 論

本文通過分析航天測量船的船搖數據特性,引入機動目標跟蹤理論進行船搖濾波及預報,針對現有模型階數不夠高的問題導出了四階的CS-Jounce模型,并給出一種機動參數自適應模型。針對船搖數據環境非高斯白噪聲的問題,引入了最大相關熵卡爾曼濾波器。實測數據分析證明,該方法能很好地跟蹤船搖數據,濾波效果較理想,預報精度較高,且能很好地估計并預報船搖角速度及角加速度。