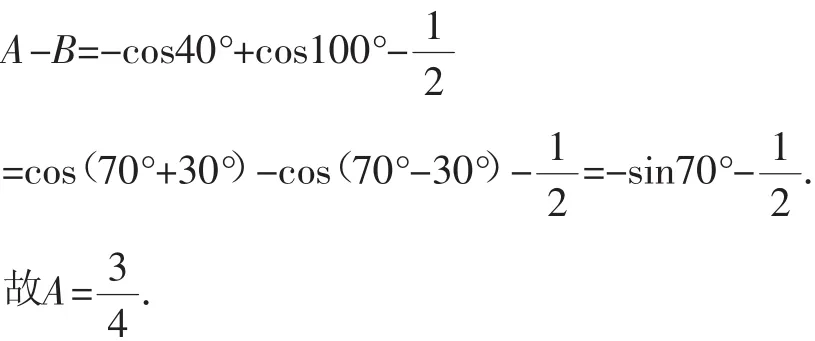例談構造法解題*

☉四川省內江師范學院數學與信息科學學院 彭玉靈

☉四川省內江師范學院數學與信息科學學院 趙思林

構造法是指依據數學中的概念和方法按固定程序經有限步解決問題的方法.強化構造思想的訓練能夠有效提高學生解題的靈活性、準確性、創造性［1］.構造法是一種富有創造性的解題方法，幾乎在數學的每一個分支中都有體現，根據數學知識內容的不同，構造法可以分為很多種，如構造方程、構造函數、構造向量、構造不等式、構造圖形、構造斜率、構造三角式、構造復數、構造二項式、構造反例、構造對偶式、構造隔板等.

一、構造方程

分析：題目中已知方程都有2個立方和33，53，將33和53分別看成方程的解，構造方程.

解：將33，53視為關于t的方程的兩個根

通分得，x（t+63）+y（t+43）=（t+43）（t+63）（t為未知數，x，y為常數），

即t2+（63+43-x-y）t+（43×63-63x-43y）=0.

由韋達定理得到63+43-x-y=-（33+53），

即x+y=33+43+53+63=432.

例2（2010年重慶卷理科）已知函數f（x）滿足：f（1），4f（x）f（y）=f（x+y）+f（x-y）（x，y∈R），則f（2010）=______.

解析：試圖尋找f（2010）與f（1）的關系，可猜想f（x）是周期函數.而按周期函數的定義f（T+x）=f（x），只出現兩次f，但所給函數方程中出現了四次且含有乘積形式4f（x）f（y），這就考慮將變量y消去，對y賦值，比如取y=1，則得f（x）=f（x+1）+f（x-1），即f（x+1）=f（x）-f（x-1）.①

那么f（x+2）=f（x+1）-f（x）.②

由①+②，得f（x+2）=-f（x-1），即f（x+3）=-f（x），則f（x+6）=f（x）.

故該函數的周期為6，則f（2010）=f（6×335+0）=f（0）.

又令x=1，y=0，得4f（1）f（0）=f（1）+f（1），

評注：此題以抽象函數和函數方程為背景，其解題思路的探究是本題的重點和難點.直覺告訴我們，f（2010）與f（1）似有聯系，這自然聯想到周期函數，由此猜想：f（x）是周期函數.而所給函數方程中含有兩個變量x，y，自然的想法是消去一個，比如取y=1，則得f（x）=f（x+1）+f（x-1），這離問題的解決就比較近了.若考生根據以往經驗簡單地猜想f（2010）=f（1）=，則是

錯誤的，這顯然是一個陷阱.本題對解題思路的探究提出了很高要求，思維難度很大，其關鍵是求出函數的周期和f（0）的值.

二、構造函數

構造函數是運用函數思想方法解決數學問題的重要手段.

例3設定義在［1，+∞）上的函數f（x）滿足xf′（x），則f（x）的最小值為______.

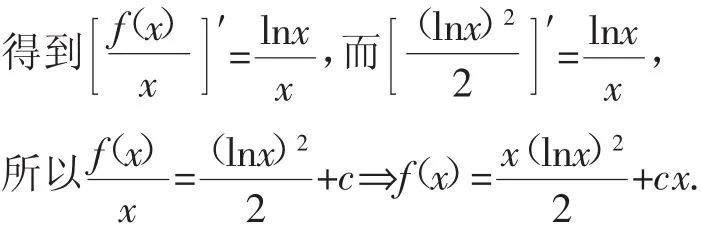
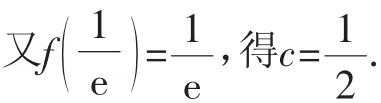
三、構造向量

向量是解決數學問題的重要工具.

證明： 構造向量m=（1，a），n=（1，b），則m-n=（0，ab），由||m|-|n||≤|m-n|，得到-|≤|a-b|，即|（fa）-（fb）|≤|a-b（|當且僅當m與n同向共線時，等號成立）.

四、構造不等式

例5設函數f（x）是定義在區間（0，1）上的正值函數，即f（x）＞0對任意x∈（0，1）都成立；不等式≤2對任意x，y∈（0，1）都成立.求證：f（x）必是常數函數.

分析：欲證明（fx）必是常數函數，只需證明（fx）=（fx0）恒成立，其中x0∈（0，1）.又考慮到條件與結論的對稱性，可以把x∈（0，1）取為中點，即取x=.問題變為需要證00明）恒成立.又由題設條件可以考慮對x，y賦值并運用二元均值不等式.

因為f（y），f（1-y）均大于0，

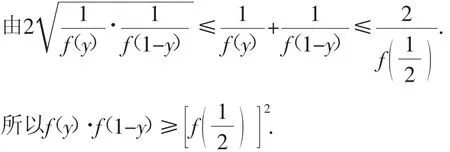
因為x，y∈（0，1），所以有故f（x）必是常數函數.

五、構造數列

六、構造圖形

構造幾何圖形是把數的問題轉化為形的問題的基本解題策略.

分析：該題初看似乎無從下手，但仔細分析兩個根式發現它們可以表示兩點的距離之和，由此構造線段來簡化問題并得到有效解決.

解：由根式聯想到距離，通過拆、湊發現f（x）可化為平方和形式，即有則該問題轉化為求點P（x，x2）到點A（2，3）與點B（0，1）距離之和的最小值.畫圖并經過觀察可知，當A，B，P在同一直線上時，|PA|+|PB|最小，其最小值為|AB|.

故（fx）min=|AB|=2.

七、構造斜率

一些具有分式結構的問題，通常可以把該分式看成兩點連線的斜率.

設切線方程為y-2=k（x+3），由圓心到切線的距離等于半徑得

評注：聯想到直線的斜率公式，將函數的最值轉化為求斜率k的范圍，使問題簡潔獲解，值得借鑒.

八、構造三角式

九、構造復數

復數具有點、向量、代數、三角等多種表示形式，且復數的幾何意義又把數與形結合起來［2］.運用復數能夠將復雜的問題簡單化，將抽象的問題具體化.

例10 設p，q，m，n∈R+，且m2+n2=1，證明：

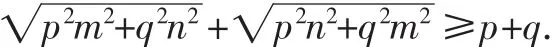
證明：設z1=pm+qni，z2=qm+pni，則

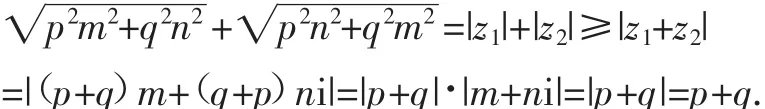
評注：從上面例題可以見得復數在解決不等式及極值中的應用，可以簡化問題及運算，為解決高考題提供又一策略.

十、構造二項式

例11 已知a，b，c∈R+且a+b+c=abc，求證an+bn+cn＞

十一、構造反例

反例是數學的精良武器.證明一個命題不成立的最好方法是構造出一個反例.

例12 （2018年北京卷文科第4題）設a，b，c，d是非零實數，則“ad=bc”是“a，b，c成等比數列”的（ ）.

A.充分而不必要條件 B.必要而不充分條件

C.充分必要條件 D.既不充分也不必要條件

解析：這里設a=d=2，c=4，d=1，此時a，b，c，d并不能構成等比數列，則可知“ad=bc”是“a，b，c成等比數列”的必要而不充分條件.

評注：此類問題在高考中均可利用構造反例來解決，可以大大減少思考和計算的時間.

十二、構造對偶式

例13 求A=sin220°+cos50°+sin20°cos50°的值.

解析：構造A的對偶式B=cos220°+sin50°+cos20°sin50°，則易得A+B=2+sin70°，